(x² +y²)²
Ôn tập chương II - Đa giác. Diện tích đa giác
\(\left(x^2+y^2\right)^2=\left(x^2\right)^2+2x^2y^2+\left(y^2\right)^2=x^4+2\left(xy\right)^2+y^4\)
Đúng 1
Bình luận (0)
Cho ▲ABC perp A,có AB6cm ,AC8CM . Kẻ đường cao AD(D thuộc BC).Đường phân giác BE cắt AD tại Fa, Vẽ hình b,Chứng minh ▲DBA đồng dạng với ▲ABC c, Tính độ dài cạnh BC,AD d, Chứng minhdfrac{ED}{FA}dfrac{EA}{EC}
Đọc tiếp
Cho ▲ABC \(\perp\) A,có AB=6cm ,AC=8CM . Kẻ đường cao AD(D thuộc BC).Đường phân giác BE cắt AD tại F
a, Vẽ hình b,Chứng minh ▲DBA đồng dạng với ▲ABC
c, Tính độ dài cạnh BC,AD d, Chứng minh\(\dfrac{ED}{FA}\)=\(\dfrac{EA}{EC}\)
b: Xét ΔDBA vuông tại D và ΔABC vuông tại A có
góc B chung
Do đo:ΔDBA đồng dạng với ΔABC
c: BC=10cm
\(AD=\dfrac{6\cdot8}{10}=4.8\left(cm\right)\)
Đúng 0
Bình luận (0)
Giải hộ bài này nha mn:
1.Chứng minh rằng : 1 tam giác là tam giác vuông nếu các chiều cao h\(_a\);h\(_b\);h\(_c\) của nó thỏa mãn điều kiện:
\(\left(\dfrac{h_a}{h_b}\right)^2+\left(\dfrac{h_a}{h_c}\right)^2=1\)
(2x-3)2+9=45
help
(2x-3)2=36
2x-3=6
2x=9
x=9/2
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông ở C, đường cao CH,các đường phân giác cắt nhau ở I. P và Q là hình chiếu của I trên AC và AB, CH cắt PQ ở N. K là trung điểm của BC. Gọi IK cắt AC ở M Chứng minh CM = CN
Cho tam giác ABC có O là giao điểm của ba đường phân giác, M là trung điểm của cạnh BC, đường cao AH cắt OM ở E, kẻ OD vuông góc với BC Chứng minh AE = OD
Ai giải giúp mik bài 4 vs ạ 
Bài V:
-ĐKXĐ: \(x\ne\pm1\).
\(\dfrac{m}{x-1}+\dfrac{x}{x+1}=\dfrac{x^2}{x^2-1}\)
\(\Leftrightarrow\dfrac{m\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}+\dfrac{x\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{x^2}{\left(x-1\right)\left(x+1\right)}\)
\(\Rightarrow mx+m+x^2-x=x^2\)
\(\Leftrightarrow m\left(x+1\right)=x\)
\(\Leftrightarrow m=\dfrac{x}{x+1}\)
-Vì m,x nguyên:
\(\Rightarrow x⋮\left(x+1\right)\)
\(\Rightarrow\left(x+1-1\right)⋮\left(x+1\right)\)
\(\Rightarrow-1⋮\left(x+1\right)\)
\(\Rightarrow\left(x+1\right)\in\left\{1;-1\right\}\)
\(\Rightarrow x\in\left\{0;-2\right\}\) (nhận)
*\(x=0\Rightarrow m=\dfrac{x}{x+1}=\dfrac{0}{0+1}=0\)
\(x=-2\Rightarrow m=\dfrac{x}{x+1}=\dfrac{-2}{-2+1}=1\)
-Vậy với \(m=0\) thì \(S=\left\{0\right\}\)
với \(m=1\) thì \(S=\left\{-2\right\}\)
Đúng 2
Bình luận (0)
a: Xét ΔADE và ΔABC có
AD/AB=AE/AC
góc A chung
=>ΔADE đồng dạng với ΔABC
b: ΔADE đồng dạg với ΔABC
=>DE/BC=AD/AB=1/2
=>BC=12cm
Đúng 0
Bình luận (0)
cho hình thang abcd có ab=5cm cd=15cm ac=16 bd=12cm từ a vẽ đường thằng song song vs bd cắt cd tại e A,chứng minh rằng tam giác ace là tam giác vuông B, tính diện tích của tứ giác abcd
a: Xét tứ giác ABDE có
AB//DE
AE//BD
=>ABDE là hbh
=>AB=DE=5cm và BD=AE=12cm
EC=5+15=20cm
EC^2=AE^2+AC^2
=>ΔAEC vuông tại A
b: Kẻ AH vuông góc EC tại H
=>AH=15*20/25=300/25=12cm
S ABCD=1/2*AH*(AB+CD)
=1/2*12*(5+15)=20*6=120cm2
Đúng 0
Bình luận (0)
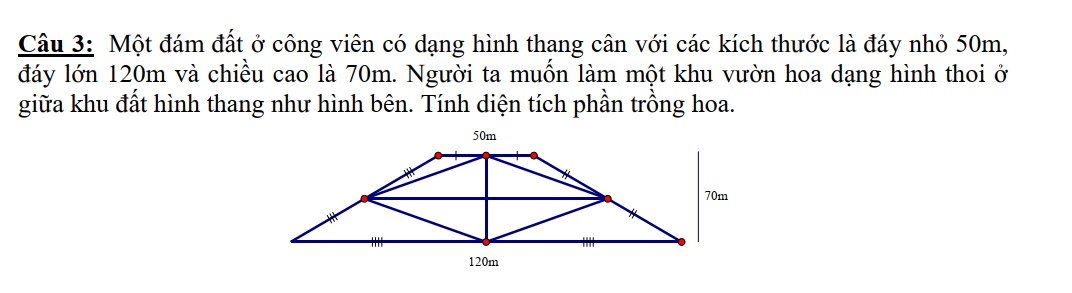
Độ dài đường chéo thứ nhất là (50+120)/2=85(m)
Diện tích phần trồng hoa là:
85*70/2=2975m2
Đúng 0
Bình luận (0)