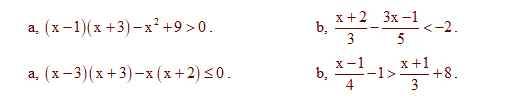`a, x^2 + 2x - 3 - x^2 + 9 >0`
`<=> 2x + 6 >0`
`<=> 2x > -6`
`<=> x > -3`.
`b, (x+2)/3 - (3x-1)/5 <-2`
`<=> (5x+10-9x+3)/15<-2`
`<=> -4x + 13 <-30`
`<=> -4x <-43`.
`<=> 4x > 43.`
`<=> x >43/4`.
`c, x^2-9 - x^2 - 2x <=0`
`<=> 9 + 2x >=0`
`<=> 2x >=-9`
`<=> x >=-9/2`.
`d, (x-1)/4 -1 > (x+1)/3 + 8`
`<=> (3x-3 -4x-4)/12>9`
`<=> -x - 7 >108`.
`<=> -x > 115`.
`<=> x <-115.`
a) \(\left(x-1\right)\left(x+3\right)-x^2+9>0\)
\(\Leftrightarrow\left(x-1\right)\left(x+3\right)-\left(x+3\right)\left(x-3\right)>0\)
\(\Leftrightarrow\left(x+3\right)\left[\left(x-1\right)-\left(x-3\right)\right]>0\)
\(\Leftrightarrow2\left(x+3\right)>0\)
\(\Leftrightarrow x+3>0\)
\(\Leftrightarrow x>-3\)
b) \(\dfrac{x+2}{3}-\dfrac{3x-1}{5}< -2\)
\(\Leftrightarrow\dfrac{5\left(x+2\right)}{15}-\dfrac{3\left(3x-1\right)}{15}< \dfrac{-2\cdot15}{15}\)
\(\Leftrightarrow5x+10-9x+3< -30\)
\(\Leftrightarrow-4x+13< -30\)
\(\Leftrightarrow-4x< -43\)
\(\Leftrightarrow x>\dfrac{43}{4}\)
\(a,\left(x-1\right)\left(x+3\right)-x^2+9>0\\ \Leftrightarrow x^2+2x-3-x^2+9>0\\ \Leftrightarrow2x>-6\\ \Leftrightarrow x>-3\)
\(b,\dfrac{x+2}{3}-\dfrac{3x-1}{5}< -2\\ \Leftrightarrow\dfrac{5\left(x+2\right)-3\left(3x-1\right)}{15}< -2\\ \Leftrightarrow5x+10-9x+3< -30\\ \Leftrightarrow-4x< -43\\ \Leftrightarrow x>\dfrac{43}{4}\)
\(a,\left(x-3\right)\left(x+3\right)-x\left(x+2\right)\le0\\ x^2-9-x^2-2x\le0\\ \Leftrightarrow-2x\le9\\ \Leftrightarrow x\ge-\dfrac{9}{2}\)
\(b,\dfrac{x-1}{4}-1>\dfrac{x+1}{3}+8\\ \Leftrightarrow\dfrac{3\left(x-1\right)-12-4\left(x+1\right)-8.12}{12}>0\\ \Leftrightarrow3x-3-12-4x-4-96>0\)
\(\Leftrightarrow-x>115\\ \Leftrightarrow x< -115\)
a) \(\left(x+3\right)\left(x-3\right)-x\left(x+2\right)\le0\)
\(\Leftrightarrow x^2-9-x^2-2x\le0\)
\(\Leftrightarrow-9-2x\le0\)
\(\Leftrightarrow2x\ge-9\)
\(\Leftrightarrow x\le-\dfrac{9}{2}\)
b) \(\dfrac{x-1}{4}-1>\dfrac{x+1}{3}+8\)
\(\Leftrightarrow\dfrac{x-5}{4}>\dfrac{x+25}{3}\)
\(\Leftrightarrow\dfrac{3\left(x-5\right)}{12}>\dfrac{4\left(x+25\right)}{12}\)
\(\Leftrightarrow3x-15>4x+100\)
\(\Leftrightarrow x< -115\)