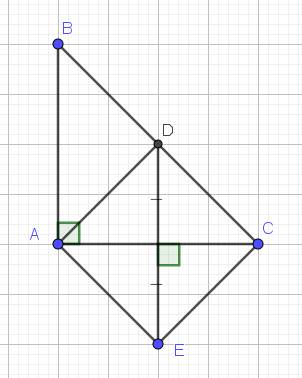
Tam giác ABC vuông tại B. Dg trung tuyến BN. Gọi M là trung điểm BA, E là điểm đối xứng với N qua M a)Cho AC=16cm Tính BN=? b) Chứng minh NC=EB c) Nếu BA=BC, cmr Tứ giác BEAN là hình vuông
Ôn tập chương II - Đa giác. Diện tích đa giác
a: BN=CA/2=8cm
b: Xét ΔBAC có AM/AB=AN/AC
nên MN//BC và MN=BC/2
=>NE//BC và NE=BC
=>BCNE là hình bình hành
=>NC=EB
c:
ΔBAC vuông cân tại B
mà BN là trung tuyến
nên BN vuông góc với AC
Xét tứ giác BNAE có
M là trung điểm chung của BA và NE
NA=NB
Do đó: BNAE là hình thoi
mà BN vuông góc với AN
nên BNAE là hình vuông
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A và M là trung điểm cạnh BC. kẻ MD vuông góc với AB (D thuộc AB) và ME vuông góc với AC (E thuộc AC)
a)chứng minh tứ giác ADME là hình chữ nhật
b)gọi P là điểm đối xứng của M qua D; Q là điểm đối xứng của M qua E . Chứng minh tứ giác PAMB là hình thoi
c)P đối xứng với Q qua A
a: Xét tứ giác ADME có
góc ADM=góc AEM=góc DAE=90 độ
nên ADME là hình chữ nhật
b: Xét tứ giác AMBP có
D là trung điểm chung của AB và MP
MA=MB
Do đó: AMBP là hình thoi
=>ABlà phân giác của góc MAP(1)
c: Xét tứ giác AMCQ có
E là trung điểm chung của AC và MQ
MA=MC
Do đó: AMCQ là hình thoi
=>AC là phân giác của góc MAQ(2)
Từ (1), (2) suy ra góc PAQ=2*90=180 độ
=>P,A,Q thẳng hàng
mà AP=AQ
nên A là trung điểm của PQ
Đúng 0
Bình luận (0)
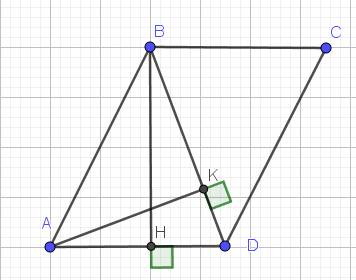
cho tam giác DEF cân tại D có đường cao DH gọi M là trung điểm của D và N là điểm đối xứng của H qua m A. biết DH = 4 cm BC = 14 cm tính diện tích tam giác DHE. B tứ giác DHFN là hình gì ? vì sao?
a: Sửa đề: EH=14cm
\(S_{DHE}=\dfrac{1}{2}\cdot4\cdot14=2\cdot14=28\left(cm^2\right)\)
b: Xét tứ giác DHFN có
M là trung điểm chung của DF và HN
góc DHF=90 độ
Do đó: DHFN là hình chữ nhật
Đúng 0
Bình luận (0)
1. Cho tam giác ABC có diện tích bằng 24cm2, đường cao AH bằng 6 cm. Tính BC
2. Cho tam giác ABC vuông cân tại A (AD là phân giác CD thuộc BC), E là điểm đối xứng với D qua AC. Tứ giác AECD là hình gì?
3. Cho tam giác nhọn ABC, các đường cao BH và CK. Gọi E và F lần lượt là hình chiếu của B và C trên HK. Chứng minh rằng EK = HF
Bài 2:
Tam giác $ABC$ cân tại $A$ nên phân giác $AD$ đồng thời là đường cao
$\Rightarrow AD\perp DC$. Mà $\widehat{DAC}=\widehat{BAC}:2 =45^0$ nên $\triangle DAC$ vuông cân tại $D$
$\Rightarrow DA=DC(1)$
$D,E$ đối xứng với nhau qua $AC$ nên $AC$ là trung trực của $DE$
$\Rightarrow CD=CE; AD=AE(2)$
Từ $(1); (2)\Rightarrow AD=DC=CE=EA$
$\Rightarrow ADCE$ là hình thoi.
Mà $\widehat{ADC}=90^0$ nên $ADCE$ là hình vuông.
Đúng 1
Bình luận (0)
Bài 3:
Xét tam giác $ABH$ và $ACK$ có:
$\widehat{AHB}=\widehat{AKC}=90^0$
$\widehat{A}$ chung
$\Rightarrow \triangle ABH\sim \triangle ACK$ (g.g)
$\Rightarrow \frac{AB}{AH}=\frac{AC}{AK}$
Xét tam giác $AKH$ và $ACB$ có:
$\widehat{A}$ chung
$\frac{AH}{AB}=\frac{AK}{AC}$ (cmt)
$\Rightarrow \triangle AKH\sim \triangle ACB$ (c.g.c)
$\Rightarrow \widehat{K_2}=\widehat{ACB}$ và $\widehat{H_1}=\widehat{ABC}$
Xét tam giác $KEB$ và $CHB$ có:
$\widehat{KEB}=\widehat{CHB}=90^0$
$\widehat{K_1}=\widehat{K_2}=\widehat{ACB}=\widehat{HCB}$ (cmt)
$\Rightarrow \triangle KEB\sim \triangle CHB$ (g.g)
$\Rightarrow \frac{KE}{KB}=\frac{CH}{CB}(1)$
Tương tự:
$\triangle CFH\sim \triangle CKB$ (c.g.c)
$\Rightarrow \frac{CH}{FH}=\frac{CB}{KB}(2)$
Từ $(1); (2)\Rightarrow \frac{KE}{KB}.\frac{CH}{FH}=\frac{CH}{CB}.\frac{CB}{KB}$
$\Rightarrow \frac{KE}{HF}=1$
$\Rightarrow KE=HF$ (đpcm)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Bạn Hoa muốn lát gạch sân vườn hình chữ nhật có chiều dài 25m và chiều rộng 4m với loại gạch hình vuông có cạnh 0,5m. Số viên gạch bạn Hoa cần mua để lát sân vườn là bao nhiêu
S\(_{sânvườn}=25.4=100\left(m^2\right)\)
S\(_{gạch}=0,5.0,5=0,25\left(m^2\right)\)
Số viên gạch =\(\dfrac{S_{sânvườn}}{S_{gạch}}=\dfrac{100}{0,25}=400viêngạch\)
Đúng 0
Bình luận (0)
 huhu giúp mình câu 4 với
huhu giúp mình câu 4 với
Lời giải:
a.
Tứ giác $ADME$ có 3 góc vuông: $\widehat{D}=\widehat{A}=\widehat{E}=90^0$ nên là hình chữ nhật.
b.
Vì $ADME$ là hcn nên $AM=DE$
$MD\perp AB, AB\perp AC\Rightarrow MD\parallel AC$. Áp dụng định lý Talet:
$\frac{BD}{DA}=\frac{BM}{MC}=1\Rightarrow BD=DA\Rightarrow D$ là trung điểm $AB$
Tương tự thì $E$ là trung điểm $AC$
$\Rightarrow DE$ là đường trung bình của tam giác $ABC$ ứng với cạnh $BC$
$\Rightarrow AM=DE=\frac{BC}{2}=\frac{\sqrt{AB^2+AC^2}}{2}=\frac{\sqrt{6^2+8^2}}{2}=5$ (cm)
c.
$S_{AMB}=\frac{BM}{BC}S_{ABC}=\frac{1}{2}S_{ABC}=\frac{1}{2}.\frac{AB.AC}{2}=\frac{6.8}{4}=12$ (cm2)
Điểm H ở đây có vẻ không có giá trị lắm.
Đúng 1
Bình luận (0)
cho tam giác ABC vuông cân ở A, biết AB=6cm, AC=8cm, kẻ AH vuông góc với BC tại H. Tính AH
BC=10cm
=>AH=6*8/10=4,8cm
Đúng 0
Bình luận (1)
Cho ΔABC vuông tại A (AB < AC). Gọi I là trung điểm của BC. Qua I vẽ IM ⊥ AB tại M và IN ⊥ AC tại N.
a) chứng minh AI=MN
a: Xét tứ giác AMIN có
góc AMI=góc ANI=góc MAN=90 độ
nên AMIN là hình chữ nhật
=>AI=MN
Đúng 1
Bình luận (0)
Cho hình bình hành ABCD, có AD = 4cm, AB = 5cm, A = 60◦ .
a) Tính S ABCD. b) Hạ AK⊥DB. Tính độ dài AK.Lời giải:
a. Kẻ $BH\perp AD$.
Có: $\frac{BH}{AB}=\sin A=\sin 60^0=\frac{\sqrt{3}}{2}$
$BH=AB.\frac{\sqrt{3}}{2}=\frac{5}{2}\sqrt{3}$
$S_{ABCD}=BH.AD=\frac{5}{2}\sqrt{3}.4=10\sqrt{3}$ (cm2)
b.
$AH=AB\cos A=5\cos 60^0=\frac{5}{2}$ (cm)
$HD=AD-AH=4-\frac{5}{2}=1,5$ (cm)
$\tan \widehat{BDA}=\tan \widehat{BDH}=\frac{BH}{HD}=\frac{5}{2}\sqrt{3}: 1,5=\frac{5\sqrt{3}}{3}$
$\Rightarrow \widehat{BDA}=70,9^0$
$\widehat{ABK}=\widehat{ABD}=180^0-\widehat{BAD}-\widehat{BDA}=180^0-60^0-70,9^0=49,1^0$
$AK=AB\sin \widehat{ABK}=5\sin 49,1^0=3,8$ (cm)
Đúng 0
Bình luận (1)