Bài 5: Trường hợp đồng dạng thứ nhất

1. Định lí

Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.

Chứng minh:

Đặt trên tia \(AB\) đoạn thẳng \(AM=A'B'\). Qua \(M\) kẻ \(MN\)//\(BC\) (\(N\in AC\))

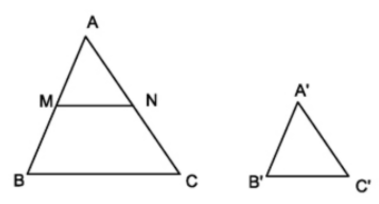
Vì \(MN\)//\(BC\) nên \(\Delta AMN\) đồng dạng với \(\Delta ABC\)

Suy ra \(\dfrac{AM}{AB}=\dfrac{AN}{AC}=\dfrac{MN}{BC}\)

Mặt khác do \(AM=A'B'\) \(\Rightarrow\) \(\dfrac{AM}{AB}=\dfrac{A'B'}{AB}\)

\(\Rightarrow\) \(\dfrac{A'B'}{AB}=\dfrac{AN}{AC}=\dfrac{MN}{BC}\)

Lại có: \(\dfrac{A'B'}{AB}=\dfrac{B'C'}{BC}=\dfrac{A'C'}{AC}\) (gt)

\(\Rightarrow\) \(\dfrac{MN}{BC}=\dfrac{B'C'}{BC}\Rightarrow MN=B'C'\)  và \(\dfrac{AN}{AC}=\dfrac{A'C'}{AC}\Rightarrow AN=A'C'\)

Từ đó ta suy ra \(\Delta AMN\) và \(\Delta A'B'C'\) có ba cạnh bằng nhau từng đôi một

Do đó: \(\Delta AMN=\Delta A'B'C'\) (c.c.c)

Vì \(\Delta AMN\) đồng dạng với \(\Delta ABC\) nên \(\Delta A'B'C'\) đồng dạng với \(\Delta ABC\).

Chú ý: Khi kí hiệu hai tam giác đồng dạng, ta cần viết đúng thứ tự các đỉnh sao cho các cặp cạnh tương ứng tỉ lệ với nhau.

Ví dụ: +) Nếu \(\Delta MNP\) và \(\Delta DEF\) có \(\dfrac{MN}{DE}=\dfrac{NP}{EF}=\dfrac{MP}{DF}\) thì ta nói \(\Delta MNP\) đồng dạng với \(\Delta DEF\);

          +) Nếu \(\Delta HIK\) và \(\Delta H'K'I'\) có \(\dfrac{HI}{H'K'}=\dfrac{IK}{K'I'}=\dfrac{HK}{H'I'}\) thì \(\Delta HIK\) đồng dạng với \(\Delta H'K'I'\);

          +) Nếu \(\Delta RSK\) và \(\Delta PQM\) có \(\dfrac{RS}{MP}=\dfrac{RK}{PQ}=\dfrac{KS}{MQ}\) thì \(\Delta RSK\) đồng dạng với \(\Delta PMQ\).

2. Áp dụng

Ví dụ 1: \(\Delta ABC\) và \(\Delta DFE\) có các cạnh như sau:

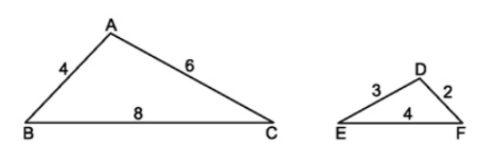
Ta thấy: \(\dfrac{AB}{DF}=\dfrac{4}{2}=2\) ; \(\dfrac{AC}{DE}=\dfrac{6}{3}=2\) ; \(\dfrac{BC}{EF}=\dfrac{8}{4}=2\)

 \(\Rightarrow\) \(\dfrac{AB}{DF}=\dfrac{AC}{DE}=\dfrac{BC}{EF}\)

Suy ra \(\Delta ABC\) đồng dạng với \(\Delta DFE\).

Ví dụ 2: Cho các cặp tam giác có độ dài lần lượt như sau. Hỏi cặp nào là cặp tam giác đồng dạng? 

a) \(3cm,5cm,7cm\) và  \(9cm,15cm,21cm\). 

b) \(4cm,6cm,7cm\) và \(2cm,3cm,4cm\).

Giải:

a) Xét các cạnh của 2 tam giác đã cho, ta thấy: \(\dfrac{3}{9}=\dfrac{5}{15}=\dfrac{7}{21}=\dfrac{1}{3}\)

Suy ra các cạnh của tam giác thứ nhất tỉ lệ với các cạnh của tam giác thứ hai

Nên 2 tam giác trên là hai tam giác đồng dạng.

b) Xét các cạnh của hai tam giác đã cho, ta thấy: \(\dfrac{4}{2}=\dfrac{6}{3}\ne\dfrac{7}{4}\)

Suy ra 2 tam giác trên không đồng dạng với nhau.

Ví dụ 3: Cho \(\Delta ABC\) đồng dạng với \(\Delta A'B'C'\). Biết rằng 3 cạnh của \(\Delta ABC\) lần lượt là \(AB=5cm\), \(BC=12cm\), \(AC=15cm\) và chu vi \(\Delta A'B'C'\) là \(24cm\). Tính độ dài các cạnh của \(\Delta A'B'C'\)?

Giải:

Ta có: Chu vi \(\Delta ABC\) là: \(P_{\Delta ABC}=5+12+15=32\left(cm\right)\)

Có \(\dfrac{P_{\Delta A'B'C'}}{P_{\Delta ABC}}=\dfrac{24}{32}=\dfrac{3}{4}\) suy ra \(\Delta A'B'C'\) đồng dạng với \(\Delta ABC\) theo tỉ số \(\dfrac{3}{4}\)

Do đó \(\dfrac{A'B'}{AB}=\dfrac{B'C'}{BC}=\dfrac{A'C'}{AC}=\dfrac{3}{4}\)

\(\Rightarrow\left\{{}\begin{matrix}\dfrac{A'B'}{5}=\dfrac{3}{4}\Rightarrow A'B'=\dfrac{15}{4}\left(cm\right)\\\dfrac{B'C'}{12}=\dfrac{3}{4}\Rightarrow B'C'=9\left(cm\right)\\\dfrac{A'C'}{15}=\dfrac{3}{4}\Rightarrow A'C'=\dfrac{45}{4}\left(cm\right)\end{matrix}\right.\)

Ví dụ 4: Cho \(\Delta ABC\) có \(AC=4\). Trên tia \(BC\) và \(AC\) lần lượt lấy các điểm \(D,E\) sao cho \(DE\)//\(AB\) và \(EC=6\). Đặt \(AB=x,DE=y\). Chứng minh \(\Delta CAB\) và \(\Delta CED\) đồng dạng?Tính tỉ số \(\dfrac{x}{y}\)?

Giải:

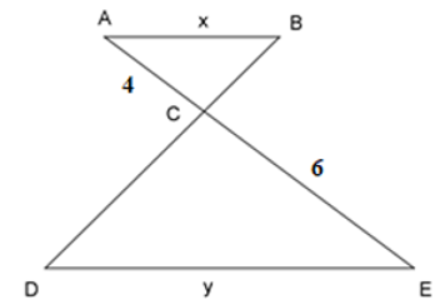
Ta có: \(D\in BC,E\in AC\) và \(DE\)//\(BC\) nên theo hệ quả của định lí Ta-lét ta có: \(\dfrac{AC}{CE}=\dfrac{BC}{CD}=\dfrac{AB}{DE}\)

Suy ra \(\Delta CAB\) đồng dạng với \(\Delta CED\) (Đpcm)

Do \(\dfrac{AC}{CE}=\dfrac{BC}{CD}=\dfrac{AB}{DE}\)

\(\Rightarrow\dfrac{x}{y}=\dfrac{4}{6}=\dfrac{2}{3}\)

Vậy \(\dfrac{x}{y}=\dfrac{2}{3}\).

Ví dụ 5: Tứ giác \(ABCD\) có \(AB=9cm\), \(BC=20cm\), \(CD=25cm\), \(AD=12cm\), \(BD=15cm\). Hỏi \(ABCD\) là hình gì?

Giải:

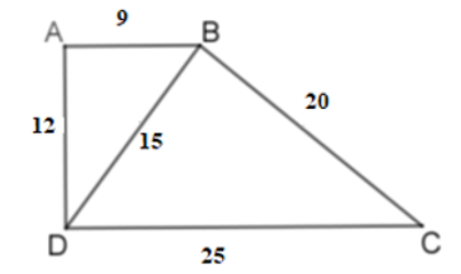
Xét \(\Delta ABD\) và \(\Delta BDC\) có:

\(\dfrac{AB}{BD}=\dfrac{9}{15}=\dfrac{3}{5}\) ; \(\dfrac{AD}{BC}=\dfrac{12}{20}=\dfrac{3}{5}\) ; \(\dfrac{BD}{DC}=\dfrac{15}{25}=\dfrac{3}{5}\)

\(\Rightarrow\) \(\dfrac{AB}{BD}=\dfrac{AD}{BC}=\dfrac{BD}{DC}\)

\(\Rightarrow\) \(\Delta ABD\) đồng dạng với \(\Delta BDC\)

Suy ra \(\widehat{ABD}=\widehat{BDC}\) (hai góc tương ứng) mà hai góc này so le trong

\(\Rightarrow\) \(AB\)//\(CD\) nên \(ABCD\) là hình thang

Mặt khác ta có: \(AB^2+AD^2=9^2+12^2=225=15^2=BD^2\)

Suy ra \(\Delta ABD\) vuông tại \(A\)

Khi đó hình thang \(ABCD\) có \(\widehat{A}=90^0\) suy ra \(ABCD\) là hình thang vuông.

Ví dụ 6. Một tam giác có cạnh nhỏ nhất là 8, hai cạnh còn lại là x và y (x<y). Tam giác thứ hai có cạnh lớn nhất là 27, hai cạnh còn lại cũng là x và y. Tính x và y để hai tam giác đó đồng dạng?

Giải:

Tam giác thứ nhất có các cạnh lần lượt là: \(8< x< y\)

Tam giác thứ hai có các cạnh lần lượt là: \(x< y< 27\)

Để hai tam giác trên đồng dạng thì \(\dfrac{8}{x}=\dfrac{x}{y}=\dfrac{y}{27}\)

Khi đó ta có: \(\left\{{}\begin{matrix}x^2=8y\\xy=8.27\end{matrix}\right.\)

Do đó: \(x^2=8y=8.\dfrac{8.27}{x}\) \(\Rightarrow x^3=8.8.27=64.27=\left(4.3\right)^3=12^3\)

\(\Rightarrow x=12\) \(\Rightarrow y=18\)

Vậy \(x=12,y=18\) thì hai tam giác đã cho đồng dạng.