Bài 3: Tính chất đường phân giác của tam giác

1. Định lí

Định lí:

Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy.

Chứng minh định lí:

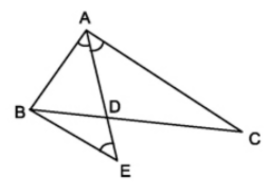
Qua \(B\) kẻ đường thẳng song song với \(AC\) cắt đường thẳng \(AD\) tại \(E\).

Ta có: \(\widehat{BAE}=\widehat{CAE}\) (do \(AD\) là tia phân giác góc \(\widehat{BAC}\))

Mặt khác: Do \(BE\)//\(AC\) \(\Rightarrow\widehat{BEA}=\widehat{CAE}\) (hai góc so le trong)

Suy ra \(\widehat{BAE}=\widehat{BEA}\) \(\Rightarrow\Delta BAE\) cân tại \(B\)

\(\Rightarrow BA=BE\)  (1)

Áp dụng hệ quả của định lí Ta-lét đối với tam giác \(DAC\), ta có: \(\dfrac{DB}{DC}=\dfrac{BE}{AC}\)  (2)

Từ (1) và (2) suy ra \(\dfrac{DB}{DC}=\dfrac{AB}{AC}\).

Ví dụ 1: Xét tam giác \(ABC\) có \(AB=3cm\), \(AC=6cm\). Tia phân giác của góc \(A\) cắt cạnh \(BC\) tại \(D\). Tính tỉ số \(\dfrac{DB}{DC}\):

Giải:

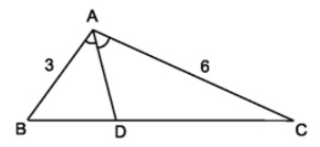
Áp dụng tính chất đường phân giác trong tam giác ta có: \(\dfrac{DB}{DC}=\dfrac{AB}{AC}\)

Lại có: \(AB=3cm\), \(AC=6cm\) \(\Rightarrow\) \(\dfrac{AB}{AC}=\dfrac{3}{6}=\dfrac{1}{2}\)

Suy ra \(\dfrac{DB}{DC}=\dfrac{1}{2}\).

Ví dụ 2: Cho tam giác \(ABC\) có \(AB=4,5cm\), \(AC=6cm\). \(AD\) là tia phân giác góc \(A\). Giả sử \(BD=x\left(cm\right)\), \(CD=y\left(cm\right)\). Tính tỉ số \(\dfrac{x}{y}\)?

Giải:

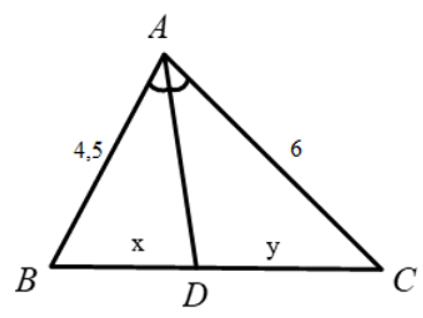
Áp dụng tính chất đường phân giác trong tam giác ta có: \(\dfrac{DB}{DC}=\dfrac{AB}{AC}\)

\(\Rightarrow\dfrac{x}{y}=\dfrac{4,5}{6}=\dfrac{3}{4}\).

Vậy \(\dfrac{x}{y}=\dfrac{3}{4}\).

Ví dụ 3: Cho tam giác \(ABC\) có \(AB=6cm\), \(AC=8cm\), \(BC=10cm\). \(AD\) là tia phân giác góc \(A\). Giả sử \(BD=x\left(cm\right)\), \(CD=y\left(cm\right)\). Tính \(x^2+y^2\)?

Giải:

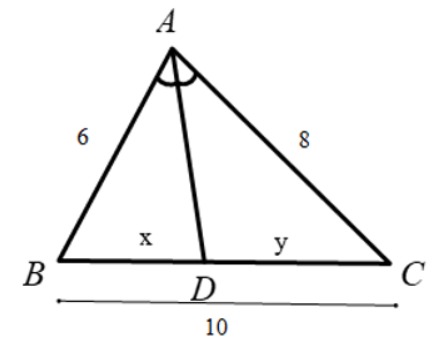
Áp dụng tính chất đường phân giác trong tam giác ta có: \(\dfrac{DB}{DC}=\dfrac{AB}{AC}\)

\(\Rightarrow\) \(\dfrac{x}{y}=\dfrac{6}{8}=\dfrac{3}{4}\)

Khi đó ta có: \(\left\{{}\begin{matrix}\dfrac{x}{y}=\dfrac{3}{4}\\x+y=10\end{matrix}\right.\) \(\Rightarrow\) \(\left\{{}\begin{matrix}x=\dfrac{10}{3+4}.3=\dfrac{30}{7}\\y=\dfrac{10}{3+4}.4=\dfrac{40}{7}\end{matrix}\right.\)

Suy ra \(x^2+y^2=\left(\dfrac{30}{7}\right)^2+\left(\dfrac{40}{7}\right)^2=\dfrac{2500}{49}\).

Ví dụ 4: Cho tam giác \(ABC\) có trung tuyến \(AM\). Gọi \(AD\), \(AE\) lần lượt là phân giác góc \(\widehat{AMB}\) và \(\widehat{AMC}\) (\(D\in AB,E\in AC\)). Chứng minh rằng: \(DE\)//\(BC\)?

Giải:

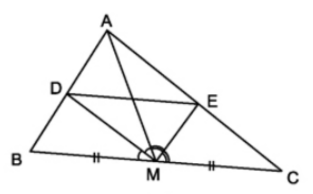
Do \(AM\) là trung tuyến của \(\Delta ABC\) \(\Rightarrow\) \(M\) là trung điểm \(BC\) \(\Rightarrow BM=CM\)

Áp dụng tính chất đường phân giác trong tam giác \(AMB\) ta có: \(\dfrac{AD}{DB}=\dfrac{AM}{BM}\)

Áp dụng tính chất đường phân giác trong tam giác \(AMC\) ta có: \(\dfrac{AE}{EC}=\dfrac{AM}{CM}\)

Do \(BM=CM\) nên \(\dfrac{AM}{BM}=\dfrac{AM}{CM}\) hay \(\dfrac{AD}{DB}=\dfrac{AE}{EC}\).

Áp dụng hệ quả của định lí Ta-lét đối với \(\Delta ABC\) ta suy ra \(DE\)//\(BC\).

Ví dụ 5: Cho \(\Delta ABC\) cân tại \(A\) có \(AB=AC=5cm\), \(BC=8cm\). \(I\) là giao điểm các đường phân giác trong tam giác. Tính \(BI?\)

Giải:

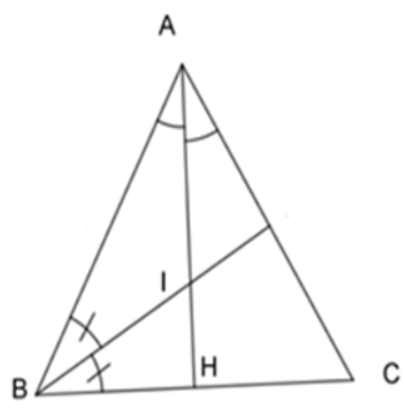
Do \(\Delta ABC\) cân tại \(A\) nên phân giác \(AH\) đồng thời là đường cao và trung tuyến của tam giác.

Suy ra \(AH\perp BC\) và \(HB=HC=\dfrac{1}{2}BC=\dfrac{1}{2}.8=4\left(cm\right)\).

Áp dụng định lí Pytago trong tam giác vuông \(HAB\) ta có: \(AH^2+HB^2=AB^2\)

\(\Rightarrow AH=\sqrt{AB^2-HB^2}=\sqrt{5^2-4^2}=3\) (cm)

Áp dụng tính chất phân giác trong tam giác \(HAB\) ta có: \(\dfrac{IA}{IH}=\dfrac{AB}{BH}\)

\(\Rightarrow\) \(\dfrac{IA}{AB}=\dfrac{IH}{BH}\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\dfrac{IA}{AB}=\dfrac{IH}{BH}=\dfrac{IA+IH}{AB+BH}=\dfrac{AH}{AB+BH}=\dfrac{3}{5+4}=\dfrac{1}{3}\)

\(\Rightarrow\dfrac{IH}{BH}=\dfrac{1}{3}\Rightarrow IH=\dfrac{1}{3}.BH=\dfrac{1}{3}.4=\dfrac{4}{3}\) (cm)

Xét \(\Delta BHI\) vuông tại \(H\). Áp dụng định lí Pytago ta có: \(BH^2+IH^2=BI^2\)

\(\Rightarrow BI=\sqrt{BH^2+IH^2}=\sqrt{4^2+\left(\dfrac{4}{3}\right)^2}=\dfrac{4\sqrt{10}}{3}\) (cm)

Vậy \(BI=\dfrac{4\sqrt{10}}{3}\left(cm\right)\).

Chú ý: Định lí vẫn đúng đối với tia phân giác của góc ngoài của tam giác.

Ví dụ: Xét tam giác \(ABC\) có \(AD'\) là tia phân giác của góc ngoài góc \(BAC\) (\(D'\in BC\))

Khi đó ta cũng có: \(\dfrac{D'B}{D'C}=\dfrac{AB}{AC}\).

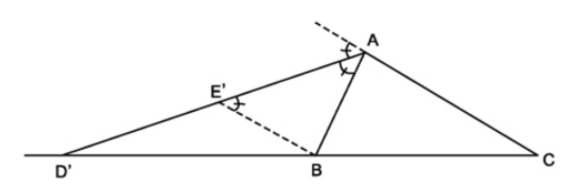
Ta có thể kẻ \(BE'\)//\(AC\) và chứng minh tương tự như trường hợp tia phân giác trong của tam giác.