Cảm ơn mọi người đã giúp đỡ ạ 
Bài 6: Ôn tập chương Đường thẳng và mặt phẳng trong không gian. Quan hệ song song.
a: \(S\in\left(SAB\right)\cap\left(SCD\right)\)
AB//CD
Do đó: \(\left(SAB\right)\cap\left(SCD\right)=Sx\)//AB//CD
b: Xét ΔSAB có SH/SA=SK/SB
nên HK//AB
=>HK//CD
mà HK ko nằm trong (SCD)
nên HK//(SCD)
Đúng 0
Bình luận (1)
Câu 8. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M là trung điểm của SA, G là trọng tâm tam giác BCD, P là điểm đối xứng với A qua B và N là điểm trên cạnh SB sao cho SN2NB. Giao điểm của đường thẳng SB và mặt phẳng (MDP) là điểm nào?A. Điểm N.B. Điểm G.C. Điểm P.D. Điểm M.Câu 9. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm của DC, BC, SA và hai điểm I, J lần lượt trên canh SB, SD sao cho SI3IB, SJ3JD. Giao điểm của đường thẳng...
Đọc tiếp
Câu 8. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M là trung điểm của SA, G là trọng tâm tam giác BCD, P là điểm đối xứng với A qua B và N là điểm trên cạnh SB sao cho SN=2NB. Giao điểm của đường thẳng SB và mặt phẳng (MDP) là điểm nào?
A. Điểm N.
B. Điểm G.
C. Điểm P.
D. Điểm M.
Câu 9. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm của DC, BC, SA và hai điểm I, J lần lượt trên canh SB, SD sao cho SI=3IB, SJ=3JD. Giao điểm của đường thẳng BC và mặt phẳng (IJP) là điểm nào?
A. Điểm I.
B. Điểm J.
C. Điểm N.
D. Điểm M.
8.
Câu này nhận xét đơn giản rằng trong 4 điểm N, G, P, M thì chỉ có duy nhất điểm N thuộc SB, do đó giao điểm của SB và (MDP) chỉ có thể là N
Nếu cần chứng minh cụ thể thì:
Ta có: P đối xứng A qua B nên B là trung điểm của AP
Lại có M là trung điểm SA
\(\Rightarrow\) Giao điểm của SB và PM là trọng tâm tam giác SAP
Mà SB là 1 trung tuyến của SAP, \(\left\{{}\begin{matrix}N\in SB\\SN=2NB\Rightarrow SN=\dfrac{2}{3}SB\end{matrix}\right.\) \(\Rightarrow N\) là trọng tâm SAP
\(\Rightarrow N\) là giao điểm SB và PM
\(\Rightarrow\left\{{}\begin{matrix}N\in SB\\N\in PM\in\left(MDP\right)\end{matrix}\right.\) \(\Rightarrow N=SB\cap\left(MDP\right)\)
Đúng 1
Bình luận (0)
9.
Tương tự câu 8, trong 4 điểm I, J, N, M chỉ duy nhất N thuộc BC nên giao điểm của BC và (IJP) là N
Cụ thể:
Trong mp (SAB), nối PI kéo dài cắt AB tại E
Áp dụng định lý Menelaus:
\(\dfrac{SP}{AP}.\dfrac{AE}{BE}.\dfrac{BI}{IS}=1\Rightarrow1.\dfrac{AE}{BE}.\dfrac{1}{3}=1\Rightarrow AE=3BE\)
\(\Rightarrow AB+BE=3BE\Rightarrow BE=\dfrac{1}{2}AB=\dfrac{1}{2}DC=CM\)
\(\Rightarrow BECM\) là hình bình hành
\(\Rightarrow ME\) cắt BC tại N là trung điểm BC (hai đường chéo hbh cắt nhau tại trung điểm mỗi đường)
Hay M, N, E thẳng hàng
Lại có: \(\dfrac{SI}{IB}=\dfrac{SJ}{JD}\Rightarrow IJ||BD\)
MN là đường trung bình tam giác BCD \(\Rightarrow MN||BD\)
\(\Rightarrow MN||IJ\)
Mà MN đi qua \(E\in PI\in\left(IJP\right)\)
\(\Rightarrow MN\subset\left(IJP\right)\Rightarrow N\in\left(IJP\right)\)
\(\Rightarrow N=BC\cap\left(IJP\right)\)
Đúng 1
Bình luận (0)
Câu 1. Cho tứ diện ABCD. Gọi I, J lần lượt là trung điểm của các cạnh AC, BC. Trên cạnh BD lấy điểm K sao cho BK2KD và E là giao điểm của JK và CD. Tìm giao điểm của đường thẳng CD và (IJK).A. Điểm I.B. Điểm J.C. Điểm E.D. Điểm K.Câu 2. Cho hình chóp S.ABCD có đáy là hình thang AB là đáy lớn. Gọi M là một điểm trên cạnh SB (M không trùng S và B), I là giao điểm của AC và BD. Giao điểm của đường thẳng DM và (SAC) làA. Giao điểm của đường thẳng DM với đường thẳng SI.B. Giao điểm của đường thẳng DM...
Đọc tiếp
Câu 1. Cho tứ diện ABCD. Gọi I, J lần lượt là trung điểm của các cạnh AC, BC. Trên cạnh BD lấy điểm K sao cho BK=2KD và E là giao điểm của JK và CD. Tìm giao điểm của đường thẳng CD và (IJK).
A. Điểm I.
B. Điểm J.
C. Điểm E.
D. Điểm K.
Câu 2. Cho hình chóp S.ABCD có đáy là hình thang AB là đáy lớn. Gọi M là một điểm trên cạnh SB (M không trùng S và B), I là giao điểm của AC và BD. Giao điểm của đường thẳng DM và (SAC) là
A. Giao điểm của đường thẳng DM với đường thẳng SI.
B. Giao điểm của đường thẳng DM với SA.
C. Giao điểm của đường thẳng DM với AC.
D. Giao điểm của đường thẳng DM với SC.
Cho tứ diện ABCD và hai điểm I, J lần lượt trên cạnh AB và AD sao cho Ij không song song với BD. xác định giao điểm Ij và( BCD)
Chọn mp(ABD) chứa đường thẳng IJ
=>BD là giao tuyến của (BCD) và (ABD)
Gọi giao của IJ và BD là M
=>M là giao điểm của IJ và (BCD)
Đúng 0
Bình luận (0)
Cứu em anh chị ơi mai em thi rồi
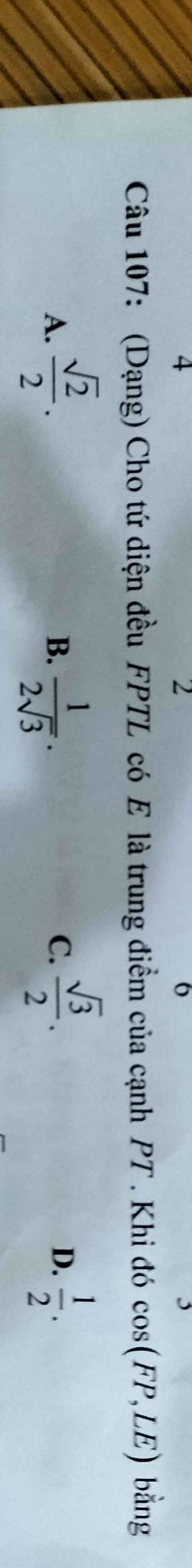
Giải đáp giúp mình nha
Đọc tiếp
Giải đáp giúp mình nha
Mọi người giải giúp em bài tập này zớii ạ💁♂️
19:
BC vuông góc AB; BC vuông góc SA
=>BC vuông góc SAB
=>BC vuông góc AH
Kẻ AH vuông góc SB
=>AH vuông góc (SBC)
=>d(A;(ABC))=AH=a*căn 3/2
1/AH^2=1/SA^2+1/AB^2
=>1/SA^2=1:(3a^2/4)-1:a^2=4/3a^2-1/a^2=1/3a^2
=>SA=a*căn 3
Đúng 0
Bình luận (0)
Cho tứ diện S.ABC có ABC là tam giác đều cạnh A, SA a và vuông góc với mặt phẳng ABC qua M là một điểm trên SC với SM x ( x lớn hơn hoặc bằng 0 và bé hơn hoặc bằng a căn 2 dựng mặt phẳng vuông góc với AB
a. Xác định góc giữa SC với mp (ABC)
b. Tính khoảng cách từ C đến mp (SAB)
c. Trình bày các diện mp (anpha)
d. Hãy xác định thiết diện tạo bởi mp (anpha) với tứ diện (SABC) và tính S thiết diện đó.
Đọc tiếp
Cho tứ diện S.ABC có ABC là tam giác đều cạnh A, SA = a và vuông góc với mặt phẳng ABC qua M là một điểm trên SC với SM = x ( x lớn hơn hoặc bằng 0 và bé hơn hoặc bằng a căn 2 dựng mặt phẳng vuông góc với AB a. Xác định góc giữa SC với mp (ABC) b. Tính khoảng cách từ C đến mp (SAB) c. Trình bày các diện mp (anpha) d. Hãy xác định thiết diện tạo bởi mp (anpha) với tứ diện (SABC) và tính S thiết diện đó.
Đề bài cho dư thừa nhiều dữ kiện quá (chắc còn các ý sau nữa)
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
Mà \(AH\in\left(SAD\right)\Rightarrow CD\perp AH\) (1)
Lại có: \(AH\perp SD\left(gt\right)\) (2)
(1);(2) \(\Rightarrow AH\perp\left(SCD\right)\)
Đúng 0
Bình luận (0)