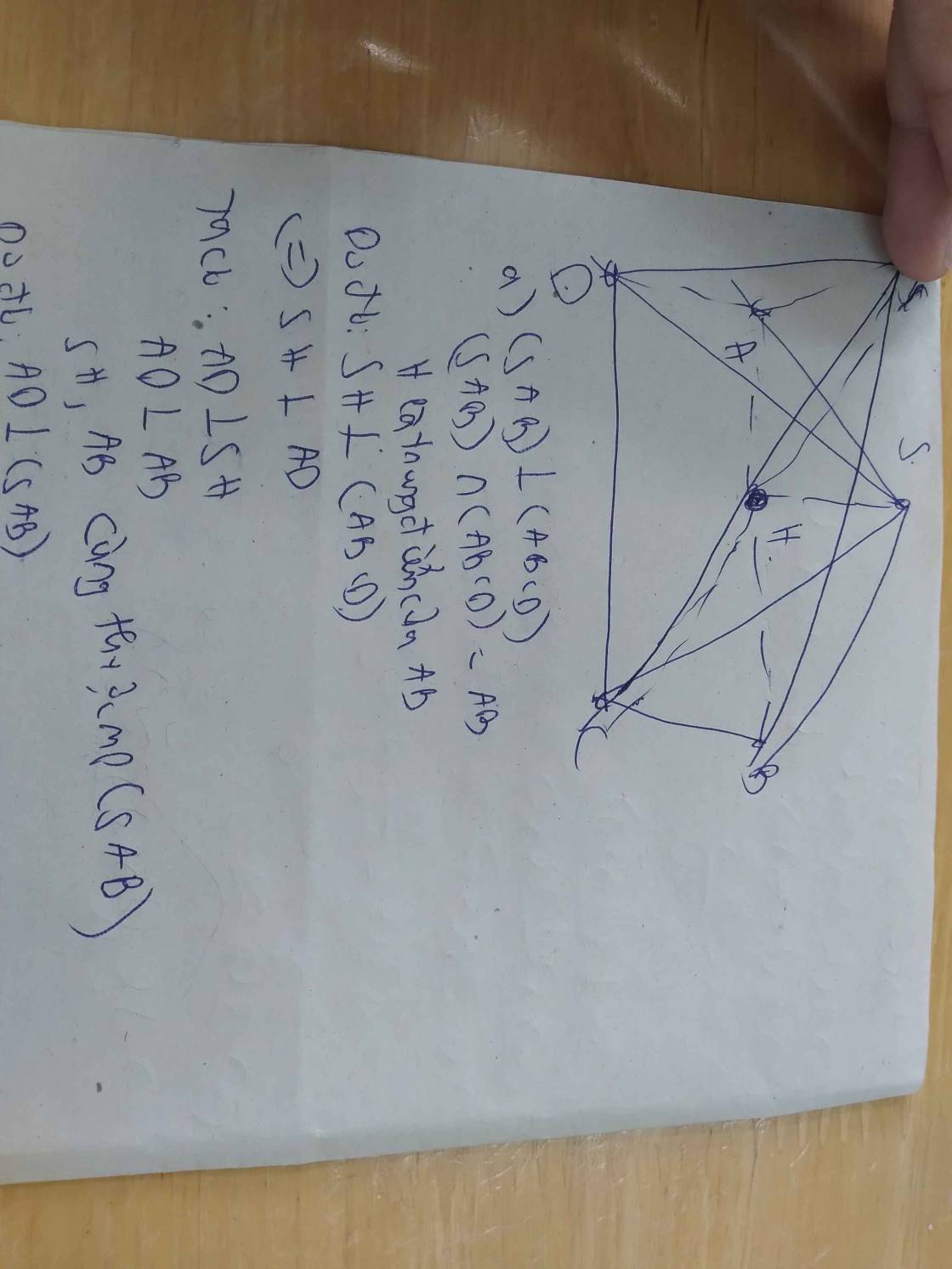
Cho hình hộp ABCD.A'B'C'D'. Xác định điểm M thuộc AC; N thuộc BD' sao cho MN// DI với I là trung điểm của AA'. Tính MA/MC
Bài 5: Phép chiếu song song. Hình biểu diễn của một hình không gian
Hic, nghĩ mãi ko thể sử dụng cách dựng hình thông thường được. Phải quay về cách sử dụng vecto mặc dù ghét cách này vì phải tính nhiều (nhưng mà nó dễ :D)
Đặt \(\overrightarrow{BA}=a;\overrightarrow{BC}=\overrightarrow{b};\overrightarrow{BB'}=\overrightarrow{c}\)
Giả sử \(\overrightarrow{AM}=x.\overrightarrow{AC}\) ; \(\overrightarrow{BN}=y.\overrightarrow{BD'}\)
Ta có: \(\overrightarrow{DI}=\overrightarrow{DA}+\overrightarrow{AI}=-\overrightarrow{b}+\dfrac{1}{2}\overrightarrow{c}\)
\(\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AB}+\overrightarrow{BN}=-x.\overrightarrow{AC}+\overrightarrow{AB}+y.\overrightarrow{BD'}=-x.\left(\overrightarrow{AB}+\overrightarrow{BC}\right)+\overrightarrow{AB}+y.\left(\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{BB'}\right)\)
\(=\left(x+y-1\right)\overrightarrow{BA}+\left(y-x\right)\overrightarrow{BC}+y.\overrightarrow{BB'}=\left(x+y-1\right)\overrightarrow{a}+\left(y-x\right)\overrightarrow{b}+y.\overrightarrow{c}\)
MN và DI song song khi và chỉ khi:
\(\left\{{}\begin{matrix}x+y-1=0\\\dfrac{y-x}{-1}=\dfrac{y}{\dfrac{1}{2}}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x+y=1\\x=3y\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}y=\dfrac{1}{4}\\x=\dfrac{3}{4}\end{matrix}\right.\)
Vậy M thuộc đoạn AC sao cho \(AM=\dfrac{3}{4}AC\) \(\Rightarrow\dfrac{AM}{MC}=3\)
N thuộc đoạn BD' sao cho \(BN=\dfrac{1}{4}BD'\)
Đúng 2
Bình luận (7)
Bài này dựng hình cũng được thôi, mà hơi làm biếng (do lúc vẽ hình kích thước lấy ko hợp lý nên đoạn kẻ thêm nó tràn ra hơi nhiều, muốn đẹp phải vẽ lại từ đầu nên cho nó next luôn).
Chuyển hình về đồng phẳng bằng cách qua D' kẻ đường song song ID cắt AD kéo dài tại E
Khi đó nối BE cắt AC ta sẽ được M và qua M kẻ đường song song D'E cắt BD' ta sẽ được N
Vậy là xong
Đúng 1
Bình luận (1)
Cho hình lăng trụ ABC.A'B'C'. Gọi M là trung điểm của BC; N là điểm trên cạnh CC' sao cho CN = 2 NC'
1) Tìm giao điểm I của AB với (A'MN). Tính IA/IB
2) tìm giao tuyến của (AMC') và (A'NB)
3) Tìm giao tuyến của (ANB) và (MA'C')
.a
Trong mp (BCC'B') nối MN kéo dài cắt BB' tại D
\(\Rightarrow D\in\left(A'MN\right)\)
Trong mp (ABB'A') nối A'D cắt AB tại I
\(\Rightarrow I=AB\cap\left(A'MN\right)\)
Do CN song song BD, áp dụng Talet:
\(\dfrac{CN}{BD}=\dfrac{CM}{BM}=1\Rightarrow CN=BD\)
\(\Rightarrow\dfrac{BD}{BB'}=\dfrac{CN}{CC'}=\dfrac{2}{3}\)
Do AA' song song BD, áp dụng Talet:
\(\dfrac{IA}{IB}=\dfrac{AA'}{BD}=\dfrac{BB'}{BD}=\dfrac{3}{2}\)
Các câu này quá nhiều đường nét nên mỗi câu 1 hình riêng cho dễ nhìn:
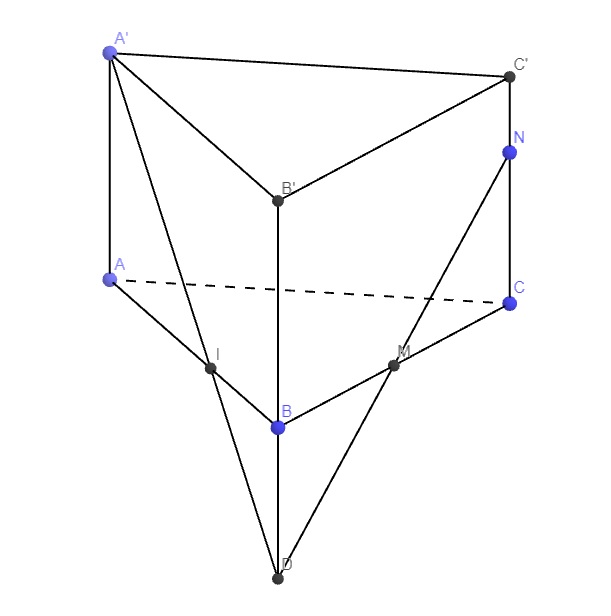
Đúng 2
Bình luận (0)
b.
Trong mp (ACC'A'), gọi E là giao điểm A'N và AC'
Trong mp ((BCC'B'), gọi F là giao điểm BN và C'M
\(\Rightarrow EF=\left(AMC'\right)\cap\left(A'NB\right)\)
c.
Trong mp (ACC'A'), kéo dài AN và A'C' cắt nhau tại G
\(\Rightarrow G\in\left(ANB\right)\cap\left(MA'C'\right)\)
\(F=BN\cap C'M\Rightarrow F\in\left(ANB\right)\cap\left(MA'C'\right)\)
\(\Rightarrow FG=\left(ANB\right)\cap\left(MA'C'\right)\)
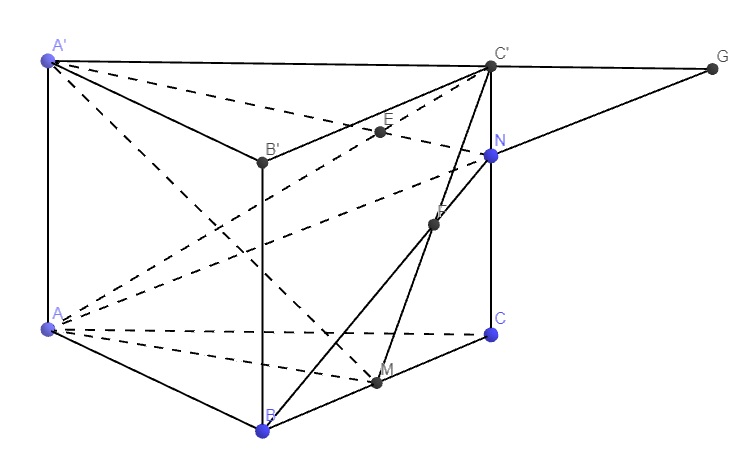
Đúng 2
Bình luận (1)
Giúp mình chứng minh phần khoanh đỏ ạ!
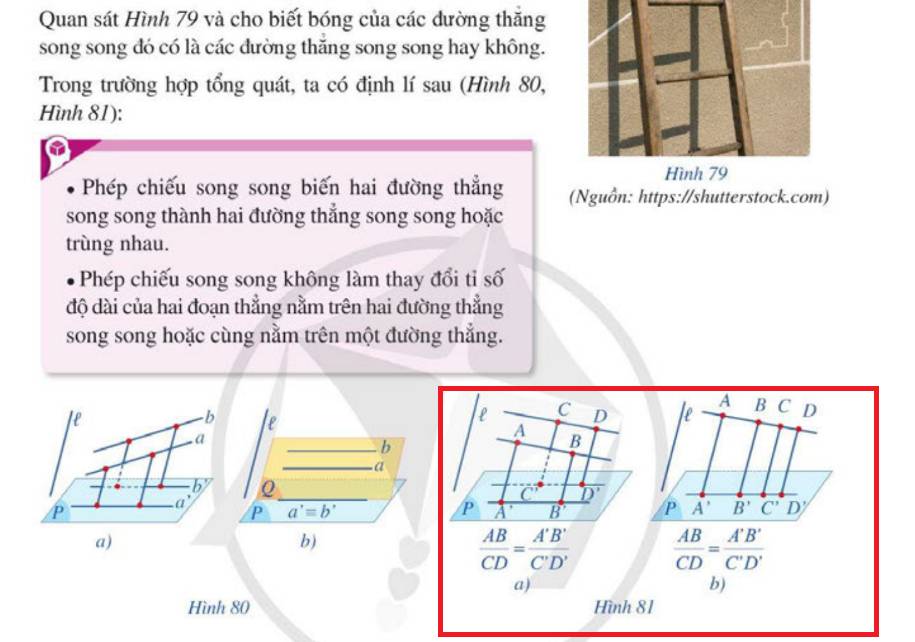
Ở hình a, em sử dụng 1 đường thẳng song song AB và CD qua B' và D' lần lượt cắt AA' và CC' tại E và F
Khi đó 2 tam giác A'B'E và C'D'F đồng dạng (3 cặp cạnh song song) nên dễ dàng suy ra đpcm
Hình b tương tự, chỉ cần qua D' kẻ 1 đường song song AD rồi lại đồng dạng là xong
Đúng 1
Bình luận (3)
cho tứ diện ABCD gọi E là trung điểm DC, M là điểm nằm giữa A và E hình chiếu song song của M lên (BCD) theo phương chiếu AD là M' khẳng định nào sau đây đúng?
A. M' thuộc đoạn BE
B. M' thuộc đoạn BC
C. M' thuộc đoạn BD
D. M' thuộc đoạn CD
Cho tứ diện ABCD gọiI J là trọng tâm tam giác ABC và ABD.E F là trung điểm của BC và AC.
a.CM IJ//CD
b.tìm giao tuyến của (DEF) và (ABD)
Ctrl/Cmd+V
Ai giúp mk vs

Giúp em giải chi tiết câu này ạ
\(AB\perp\left(BCD\right)\Rightarrow BD\) là hình chiếu vuông góc của AD lên (BCD)
\(\Rightarrow\widehat{ADB}\) là góc giữa AD và (BCD)
\(tan\widehat{ADB}=\dfrac{AB}{BD}=\sqrt{3}\Rightarrow\widehat{ADB}=60^0\)
Đúng 0
Bình luận (0)