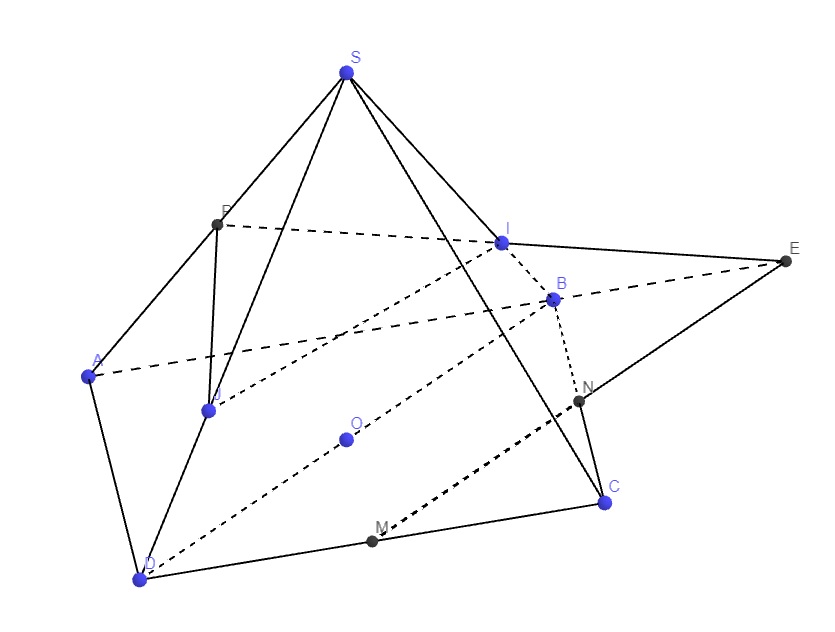
Câu 8. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M là trung điểm của SA, G là trọng tâm tam giác BCD, P là điểm đối xứng với A qua B và N là điểm trên cạnh SB sao cho SN=2NB. Giao điểm của đường thẳng SB và mặt phẳng (MDP) là điểm nào?
A. Điểm N.
B. Điểm G.
C. Điểm P.
D. Điểm M.
Câu 9. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm của DC, BC, SA và hai điểm I, J lần lượt trên canh SB, SD sao cho SI=3IB, SJ=3JD. Giao điểm của đường thẳng BC và mặt phẳng (IJP) là điểm nào?
A. Điểm I.
B. Điểm J.
C. Điểm N.
D. Điểm M.
8.
Câu này nhận xét đơn giản rằng trong 4 điểm N, G, P, M thì chỉ có duy nhất điểm N thuộc SB, do đó giao điểm của SB và (MDP) chỉ có thể là N
Nếu cần chứng minh cụ thể thì:
Ta có: P đối xứng A qua B nên B là trung điểm của AP
Lại có M là trung điểm SA
\(\Rightarrow\) Giao điểm của SB và PM là trọng tâm tam giác SAP
Mà SB là 1 trung tuyến của SAP, \(\left\{{}\begin{matrix}N\in SB\\SN=2NB\Rightarrow SN=\dfrac{2}{3}SB\end{matrix}\right.\) \(\Rightarrow N\) là trọng tâm SAP
\(\Rightarrow N\) là giao điểm SB và PM
\(\Rightarrow\left\{{}\begin{matrix}N\in SB\\N\in PM\in\left(MDP\right)\end{matrix}\right.\) \(\Rightarrow N=SB\cap\left(MDP\right)\)
9.
Tương tự câu 8, trong 4 điểm I, J, N, M chỉ duy nhất N thuộc BC nên giao điểm của BC và (IJP) là N
Cụ thể:
Trong mp (SAB), nối PI kéo dài cắt AB tại E
Áp dụng định lý Menelaus:
\(\dfrac{SP}{AP}.\dfrac{AE}{BE}.\dfrac{BI}{IS}=1\Rightarrow1.\dfrac{AE}{BE}.\dfrac{1}{3}=1\Rightarrow AE=3BE\)
\(\Rightarrow AB+BE=3BE\Rightarrow BE=\dfrac{1}{2}AB=\dfrac{1}{2}DC=CM\)
\(\Rightarrow BECM\) là hình bình hành
\(\Rightarrow ME\) cắt BC tại N là trung điểm BC (hai đường chéo hbh cắt nhau tại trung điểm mỗi đường)
Hay M, N, E thẳng hàng
Lại có: \(\dfrac{SI}{IB}=\dfrac{SJ}{JD}\Rightarrow IJ||BD\)
MN là đường trung bình tam giác BCD \(\Rightarrow MN||BD\)
\(\Rightarrow MN||IJ\)
Mà MN đi qua \(E\in PI\in\left(IJP\right)\)
\(\Rightarrow MN\subset\left(IJP\right)\Rightarrow N\in\left(IJP\right)\)
\(\Rightarrow N=BC\cap\left(IJP\right)\)