Câu 4:
1: Gọi AB là chiều cao của tháp; D,C lần lượt là điểm mà anh trên tháp thấy xe máy đang chạy.
Theo đề, ta có: AB=100m; AB\(\perp\)DB tại B; \(\widehat{ADB}=30^0;\widehat{ACB}=60^0\)
Xét ΔABD vuông tại B có \(sinD=\dfrac{AB}{AD}\)
=>\(\dfrac{100}{AD}=sin30=\dfrac{1}{2}\)
=>\(AD=200\left(m\right)\)
Ta có: ΔABD vuông tại B
=>\(BA^2+BD^2=AD^2\)
=>\(BD^2=200^2-100^2=30000\)
=>\(BD=100\sqrt{3}\left(m\right)\)
Ta có: \(\widehat{ACB}+\widehat{ACD}=180^0\)(hai góc kề bù)
=>\(\widehat{ACD}=180^0-60^0=120^0\)
Xét ΔCAD có \(\widehat{D}+\widehat{ACD}+\widehat{CAD}=180^0\)
=>\(\widehat{CAD}+120^0+30^0=180^0\)
=>\(\widehat{CAD}=30^0\)
Xét ΔCAD có \(\dfrac{AD}{sinACD}=\dfrac{DC}{sinDAC}\)
=>\(\dfrac{200}{sin120}=\dfrac{DC}{sin30}\)
=>\(DC=\dfrac{200\sqrt{3}}{3}\left(m\right)\)
=>Sau 6 phút thì xe máy đi được quãng đường là \(\dfrac{200\sqrt{3}}{3}\left(m\right)\)
Vận tốc của xe máy là: \(\dfrac{200\sqrt{3}}{3}:6=\dfrac{200\sqrt{3}}{18}=\dfrac{100\sqrt{3}}{9}\left(\dfrac{m}{p}\right)\)
Thời gian xe máy đến chân tháp là:
\(100\sqrt{3}:\dfrac{100\sqrt{3}}{9}=9\left(phút\right)\)
2:
a: ΔDAC vuông tại D
=>\(AC^2=DA^2+DC^2\)
=>\(AC^2=6^2+8^2=100\)
=>\(AC=\sqrt{100}=10\left(cm\right)\)
Xét ΔDAC vuông tại D có DH là đường cao
nên \(DH\cdot AC=DA\cdot DC\)
=>\(DH\cdot10=6\cdot8=48\)
=>DH=48/10=4,8(cm)
Xét ΔADC vuông tại D có \(sinACD=\dfrac{AD}{AC}=\dfrac{6}{10}=\dfrac{3}{5}\)
nên \(\widehat{ACD}\simeq36^052'\)
b: Xét ΔDAC vuông tại D có DH là đường cao
nên \(AH\cdot AC=AD^2;CH\cdot CA=CD^2\)
=>\(\dfrac{AH\cdot AC}{CH\cdot AC}=\dfrac{AD^2}{CD^2}\)
=>\(\dfrac{AH}{CH}=\dfrac{BC^2}{AB^2}=\left(\dfrac{BC}{AB}\right)^2\)
c: Gọi K là trung điểm của DH
Xét ΔHAD có
F,K lần lượt là trung điểm của HA,HD
=>FK là đường trung bình của ΔHAD
=>FK//AD và \(FK=\dfrac{AD}{2}\)
ta có: FK//AD
AD\(\perp\)DC
Do đó: FK\(\perp\)DC
Xét ΔFDC có
FK,DH là các đường cao
FK cắt DH tại K
Do đó: K là trực tâm của ΔFDC
=>FK\(\perp\)DC
Ta có: FK//AD
BC//AD
Do đó: FK//BC
Ta có: \(FK=\dfrac{AD}{2}\)
\(CE=\dfrac{CB}{2}\)
mà AD=CB
nên FK=CE
Xét tứ giác FKCE có
FK//CE
FK=CE
Do đó: FKCE là hình bình hành
=>CK//FE
Ta có: CK//FE
CK\(\perp\)FD
Do đó: FE\(\perp\)FD



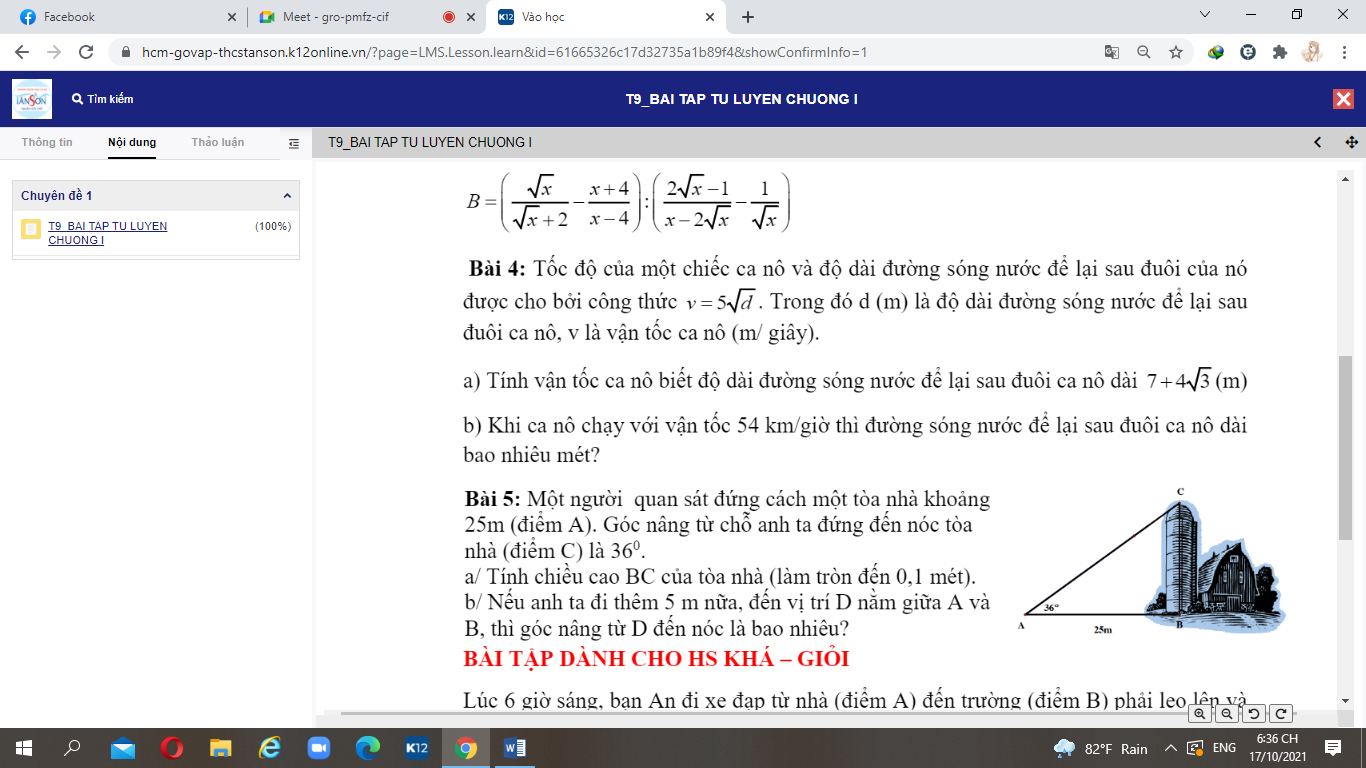

 (Với x > 0; x 1; x4)
(Với x > 0; x 1; x4)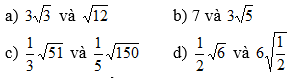
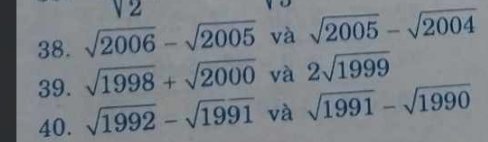 giúm mình bài này v ạ so sánh ạ mình camon
giúm mình bài này v ạ so sánh ạ mình camon