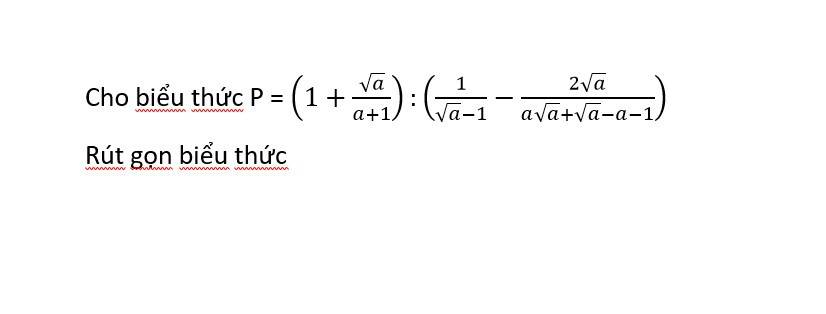\(\dfrac{\left(a\sqrt{b}+b\right)\left(\sqrt{a}+\sqrt{b}\right)}{a-b}\sqrt{\dfrac{ab+b^2-2\sqrt{ab^3}3}{a\left(a+2\sqrt{b}\right)+b}}\)
Bài 6: Biến đối đơn giản biểu thức chứa căn bậc hai
Sửa đề: \(\dfrac{\left(a\sqrt{b}+b\right)\left(\sqrt{a}+\sqrt{b}\right)}{a-b}\cdot\sqrt{\dfrac{ab+b^2-2\sqrt{ab^3}}{a\left(a+2\sqrt{b}\right)+b}}\)
Đặt \(A=\dfrac{\left(a\sqrt{b}+b\right)\left(\sqrt{a}+\sqrt{b}\right)}{a-b}\cdot\sqrt{\dfrac{ab+b^2-2\sqrt{ab^3}}{a\left(a+2\sqrt{b}\right)+b}}\)
ĐKXĐ: a>0 và b>0 và a<>b
\(A=\dfrac{\left(a\sqrt{b}+b\right)\left(\sqrt{a}+\sqrt{b}\right)}{a-b}\cdot\sqrt{\dfrac{ab+b^2-2\sqrt{ab^3}}{a\left(a+2\sqrt{b}\right)+b}}\)
\(=\dfrac{\sqrt{b}\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}{\left(\sqrt{a}-\sqrt{b}\right)\cdot\left(\sqrt{a}+\sqrt{b}\right)}\cdot\sqrt{\dfrac{ab+b^2-2\sqrt{ab}\cdot b}{a^2+2a\sqrt{b}+b}}\)
\(=\dfrac{\sqrt{b}\left(\sqrt{a}+\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}\cdot\sqrt{\dfrac{\left(\sqrt{ab}-b\right)^2}{\left(a+\sqrt{b}\right)^2}}\)
\(=\dfrac{\sqrt{b}\left(\sqrt{a}+\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}\cdot\dfrac{\sqrt{ab}-b}{\sqrt{a}+\sqrt{b}}\)
\(=\dfrac{\sqrt{b}\left(\sqrt{ab}-b\right)}{\sqrt{a}-\sqrt{b}}=\dfrac{b\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}\)
=b
Đúng 0
Bình luận (0)
\(P=\left(1+\dfrac{\sqrt{a}}{a+1}\right):\left(\dfrac{1}{\sqrt{a}-1}-\dfrac{2\sqrt{a}}{a\sqrt{a}+\sqrt{a}-a-1}\right)\\ P=\dfrac{a+\sqrt{a}+1}{a+1}:\left(\dfrac{1}{\sqrt{a}-1}-\dfrac{2\sqrt{a}}{a\left(\sqrt{a}-1\right)+\left(\sqrt{a}-1\right)}\right)\\ P=\dfrac{a+\sqrt{a}+1}{a+1}:\dfrac{a+1+2\sqrt{a}}{\left(\sqrt{a}-1\right)\left(a+1\right)}\\ P=\dfrac{a+\sqrt{a}+1}{a+1}:\dfrac{\left(\sqrt{a}+1\right)^2}{\left(\sqrt{a}-1\right)\left(a+1\right)}\\ P=\dfrac{a+\sqrt{a}+1}{a+1}\cdot\dfrac{\left(\sqrt{a}-1\right)\left(a+1\right)}{\left(\sqrt{a}+1\right)^2}\\ P=\dfrac{\sqrt{a^3}-1}{\left(\sqrt{a}+1\right)^2}\)
Đúng 2
Bình luận (1)
\(\left(\dfrac{10+2\sqrt{10}}{\sqrt{5}+\sqrt{2}}+\dfrac{\sqrt{30}-\sqrt{6}}{\sqrt{5}-1}\right)\) : \(\dfrac{1}{2\sqrt{5}-\sqrt{6}}\) =?
\(\left(\dfrac{10+2\sqrt{10}}{\sqrt{5}+\sqrt{2}}+\dfrac{\sqrt{30}-\sqrt{6}}{\sqrt{5}-1}\right):\dfrac{1}{2\sqrt{5}-\sqrt{6}}\)
\(=\left(\dfrac{2\sqrt{5}\cdot\sqrt{5}+\sqrt{2}\cdot2\sqrt{5}}{\sqrt{5}+\sqrt{2}}+\dfrac{\sqrt{5}\cdot\sqrt{6}-\sqrt{6}\cdot1}{\sqrt{5}-1}\right):\dfrac{1}{2\sqrt{5}-\sqrt{6}}\)
\(=\left[\dfrac{2\sqrt{5}\left(\sqrt{5}+\sqrt{2}\right)}{\sqrt{5}+\sqrt{2}}+\dfrac{\sqrt{6}\left(\sqrt{5}-1\right)}{\sqrt{5}-1}\right]\cdot\left(2\sqrt{5}-\sqrt{6}\right)\)
\(=\left(2\sqrt{5}+\sqrt{6}\right)\left(2\sqrt{5}-\sqrt{6}\right)\)
\(=\left(2\sqrt{5}\right)^2-\left(\sqrt{6}\right)^2\)
\(=20-6\)
\(=14\)
Đúng 1
Bình luận (0)
\(=\left(\dfrac{2\sqrt{5}\left(\sqrt{5}+\sqrt{2}\right)}{\sqrt{5}+\sqrt{2}}+\dfrac{\sqrt{6}\left(\sqrt{5}-1\right)}{\sqrt{5}-1}\right)\cdot\left(2\sqrt{5}-\sqrt{6}\right)\)
\(=\left(2\sqrt{5}+\sqrt{6}\right)\left(2\sqrt{5}-\sqrt{6}\right)\)
=20-6
=14
Đúng 0
Bình luận (0)
\(\left(\dfrac{\sqrt{14}-\sqrt{7}}{1-\sqrt{2}}+\dfrac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}\right)\) : \(\dfrac{1}{\sqrt{7}-\sqrt{5}}\) =?
\(=\left(\dfrac{\sqrt{7}\left(\sqrt{2}-1\right)}{1-\sqrt{2}}+\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{1-\sqrt{3}}\right).\left(\sqrt{7}-\sqrt{5}\right)\\=\left(-\dfrac{\sqrt{7}\left(1-\sqrt{2}\right)}{1-\sqrt{2}}-\dfrac{\sqrt{5}\left(1-\sqrt{3}\right)}{1-\sqrt{3}}\right)\left(\sqrt{7}-\sqrt{5}\right)\\ =\left(-\sqrt{7}-\sqrt{5}\right)\left(\sqrt{7}-\sqrt{5}\right)\\ =-\left(\sqrt{7}+\sqrt{5}\right)\left(\sqrt{7}-\sqrt{5}\right)\\ =-\left(7-5\right)\\ =-2\)
Đúng 3
Bình luận (0)
7+ căn 9x^2-6x+1=2x
\(\Leftrightarrow7+\sqrt{\left(3x-1\right)^2}=2x\)
=>|3x-1|=2x-7
=>x>=7/2 và (3x-1)^2=(2x-7)^2
=>x>=7/2 và (3x-1-2x+7)(3x-1+2x-7)=0
=>x>=7/2 và (x+6)(5x-8)=0
=>x>=7/2 và (x=-6 hoặc x=8/5)
=>\(x\in\varnothing\)
Đúng 0
Bình luận (0)
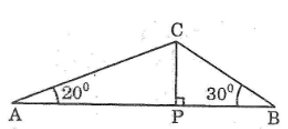
Tam giác ABC có A , B , AB 60cm. Đường vuông góc kẻ từ C đến AB cắt AB tại P. Hãy tìm: AP, BP,CP và S tam giác ABC.giúp mình với ạ
Đọc tiếp
Tam giác ABC có A =
,
B =
, AB = 60cm. Đường vuông góc kẻ từ C đến AB cắt AB tại P. Hãy tìm: AP, BP,CP và S tam giác ABC.
giúp mình với ạ
góc ACB=180-20-30=130 độ
Xét ΔABC có
AB/sinC=AC/sinB=BC/sinA
=>BC/sin20=AC/sin30=60/sin130
=>\(BC\simeq26,79\left(cm\right);AC\simeq39,16\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}\cdot BC\cdot BA\cdot sinBCA\)
\(=\dfrac{1}{2}\cdot39.16\cdot26.79\cdot sin130=401.83\left(cm^2\right)\)
\(CP=2\cdot\dfrac{S_{ABC}}{AB}=\dfrac{2\cdot401.83}{60}\simeq13,39\left(cm\right)\)
Xét ΔCPA vuông tại P có
tan A=CP/AP
=>13,39/AP=tan20
=>\(AP\simeq36.79\left(cm\right)\)
PB=AB-AP=60-36,79=23,21cm
Đúng 0
Bình luận (0)
sqrt(18 + 12sqrt(2)) giúp e vs ạ
\(\sqrt{18+12\sqrt{2}}\)
\(=\sqrt{6\cdot\left(3+2\sqrt{2}\right)}\)
\(=\sqrt{6\cdot\left[\left(\sqrt{2}\right)^2+2\cdot\sqrt{2}\cdot1+1^2\right]}\)
\(=\sqrt{6\left(\sqrt{2}+1\right)^2}\)
\(=\sqrt{6}\cdot\left|\sqrt{2}+1\right|\)
\(=\sqrt{6}\cdot\left(\sqrt{2}+1\right)\)
\(=\sqrt{12}+\sqrt{6}\)
\(=2\sqrt{3}+\sqrt{6}\)
Đúng 3
Bình luận (0)
\(\sqrt{18+12\sqrt{2}}\)
\(=\sqrt{6\left(3+2\sqrt{2}\right)}=\sqrt{\left(\sqrt{6}\cdot\sqrt{2}+\sqrt{6}\right)^2}\)
\(=\left|\sqrt{12}+\sqrt{6}\right|=2\sqrt{3}+\sqrt{6}\)
Đúng 0
Bình luận (0)
Bài 1: Đưa thừa số ra ngoài dấu căn a, 3 nhân căn bậc 200= b, -5 nhân căn bậc 50 nhân a mũ 2 nhân b mũ 2 C, - căn bậc 75 nhân a mũ 2 nhân b mũ 3
a: \(3\sqrt{200}=3\cdot10\sqrt{2}=30\sqrt{2}\)
b: \(-5\sqrt{50a^2b^2}=-5\cdot5\sqrt{2a^2b^2}\)
\(=-25\cdot\left|ab\right|\cdot\sqrt{5}\)
c: \(-\sqrt{75a^2b^3}\)
\(=-\sqrt{25a^2b^2\cdot3b}=-5\left|ab\right|\cdot\sqrt{3b}\)
Đúng 2
Bình luận (0)
1, rút gọn
g, \(\sqrt{5a}\) - \(\sqrt{16a}\) + \(\sqrt{49a}\) (a>=0)
m, \(\dfrac{20}{3+\sqrt{5}+\sqrt{2+2\sqrt{5}}}\)
g: \(=\sqrt{5a}-4\sqrt{a}+7\sqrt{a}\)
\(=\sqrt{5a}+3\sqrt{a}\)
b: \(=\dfrac{40}{6+2\sqrt{5}+2\cdot\sqrt{2+2\sqrt{5}}}\)
\(=\dfrac{40}{\left(\sqrt{5}+1\right)^2+\sqrt{2}\cdot\sqrt{4+4\sqrt{5}}}\)
\(=\dfrac{40}{\left(\sqrt{5}+1\right)^2+2\sqrt{2}\cdot\sqrt{\sqrt{5}+1}}\)
\(=\dfrac{40}{\left(\sqrt{\sqrt{5}+1}\right)\left[\left(\sqrt{\sqrt{5}+1}\right)^3+2\sqrt{2}\right]}\)
Đúng 0
Bình luận (0)
1. rút gọn
a, \(\sqrt{54a}\) - \(\sqrt{16a}\) + \(\sqrt{49a}\) (a>0)
m, \(\dfrac{20}{3+\sqrt{5}+\sqrt{2+2\sqrt{5}}}\)
nếu câu a sai thì hãy làm câu b nhé