Giúp mình với ạ, mình cảm ơn.
Bài 5: Phép quay
mng em trình bày lý thuyết biểu thức tọa độ vậy đúng chưa ạ, góc OM là alpha thì góc OM' là góc gì v ạ
Góc quay \(\alpha\) là góc \(\widehat{MOM'}\) , không phải góc \(\widehat{xOM}\) đâu em
Hơn nữa phép quay tâm O như hình vẽ thì 2 đoạn OM=OM', trong hình thấy có vẻ ko dài bằng nhau lắm :D
Đúng 1
Bình luận (1)
Giúp em vs ạ
Vì (d') là ảnh của (d) qua Q(0;-90 độ)
nên (d'): 4x+y+c=0
Gọi A(3;1) thuộc (d)
Tọa độ A' là:
\(\left\{{}\begin{matrix}x=3\cdot cos\left(-90^0\right)-1\cdot sin\left(-90^0\right)=1\\y=3\cdot sin\left(-90^0\right)+1\cdot cos\left(-90^0\right)=-3\end{matrix}\right.\)
Thay x=1 và y=-3 vào (d'), ta được:
c+4+3=0
=>c=-7
Đúng 2
Bình luận (0)
Giúp em vs ạ
3: Lấy A(-1;-1) thuộc d
Tọa độ A' là:
\(\left\{{}\begin{matrix}x=-1\cdot cos90^0-\left(-1\right)\cdot sin90^0=1\\y=-1\cdot sin90^0+\left(-1\right)\cdot cos90^0=-1\end{matrix}\right.\)
Vì (d') là ảnh của (d) qua Q(0;90 độ)
nên (d'): -2x+3y+c=0
Thay x=1 và y=-1 vào (d'), ta được:
c-2-3=0
=>c=5
Đúng 0
Bình luận (0)
3.
Pt d là \(3x+2y+5=0\) đúng ko nhỉ?
Lấy \(A\left(-1;-1\right)\) và \(B\left(3;-7\right)\) là 2 điểm thuộc d
\(Q_{\left(O;90^0\right)}\left(A\right)=A'\left(x';y'\right)\Rightarrow\left\{{}\begin{matrix}x'=1\\y'=-1\end{matrix}\right.\)
\(Q_{\left(0;90^0\right)}\left(B\right)=B'\left(x_1;y_1\right)\Rightarrow\left\{{}\begin{matrix}x_1=7\\y_1=3\end{matrix}\right.\)
\(\Rightarrow A';B'\in d'\) với \(d'=Q_{\left(O;90^0\right)}\left(d\right)\)
\(\overrightarrow{A'B'}=\left(6;4\right)=2\left(3;2\right)\)
\(\Rightarrow\) Đường thẳng d' nhận \(\left(2;-3\right)\) là 1 vtpt
Phương trình d':
\(2\left(x-1\right)-3\left(y+1\right)=0\Leftrightarrow2x-3y-5=0\)
Câu 4 tương tự
Đúng 1
Bình luận (0)
D mới là đáp án đúng do đường thẳng \(y=x\) hợp với trục Ox 1 góc 45 độ (có chiều ngược chiều kim đồng hồ)
Đúng 1
Bình luận (0)
`d:x-y-4=0` và `I(1;1)`
Gọi `A(0;-4)` và `B(4;0) in d`
`Q_{(I,-\pi/2)} (A)=A'=>`$\begin{cases} x_{A'}-1=(0-1)cos \dfrac{-\pi}{2}-(-4-1)sin \dfrac{-\pi}{2}<=>x_{A'}=-4\\y_{A'}-1=(0-1)sin\dfrac{-\pi}{2}+(-4-1)cos\dfrac{-\pi}{2}<=>y_{A'}=2 \end{cases}$
`=>A'(-4;2)`
`Q_{(I,-\pi/2)} (B)=B'=>`$\begin{cases} x_{B'}-1=(4-1)cos \dfrac{-\pi}{2}-(0-1)sin \dfrac{-\pi}{2}<=>x_{B'}=0\\y_{B'}-1=(4-1)sin\dfrac{-\pi}{2}+(0-1)cos\dfrac{-\pi}{2}<=>y_{B'}=-2 \end{cases}$
`=>B'(0;-2)`
Vì `(d')` là ảnh của `(d)=>A'B' in (d')`
Có: `\vec{A'B'}=(4;-4)-` là vtcp của `(d')`
`=>`Vtpt của `(d')` là: `(1;1)` mà `B(0;-2) in (d')`
`=>` Ptr `(d')` là: `1(x-0)+1(y+2)=0<=>x+y+2=0`
`->\bb B`
Đúng 2
Bình luận (0)
Đường tròn (C) tâm \(I\left(2;1\right)\) bán kính \(R=\sqrt{2^2+1^2-1}=2\)
\(\Rightarrow\left(C'\right)\) có \(R'=R=2\) và tâm \(I'\left(x';y'\right)=T_{\overrightarrow{v}}\left(I\right)\)
\(\left\{{}\begin{matrix}x'=2+1=3\\y'=1+3=4\end{matrix}\right.\)
\(\Rightarrow\left(C'\right)\): \(\left(x-3\right)^2+\left(y-4\right)^2=4\)
Đúng 1
Bình luận (0)
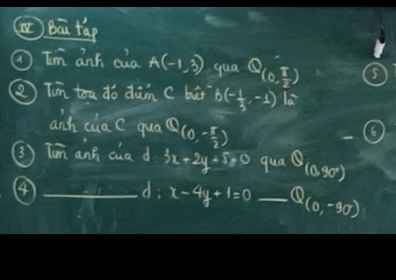 Giúp em câu 3,4 vs ạ
Giúp em câu 3,4 vs ạ
4:
Gọi A(3;1) thuộc (d)
Tọa độ A' là:
\(\left\{{}\begin{matrix}x=3\cdot cos\left(-90^0\right)-1\cdot sin\left(-90^0\right)=1\\y=3\cdot sin\left(-90^0\right)+1\cdot cos\left(-90^0\right)=-3\end{matrix}\right.\)
(d'): x-4y+a=0
Thay x=1 và y=-3 vào (d'), ta được:
a+1+12=0
=>a=-13
Đúng 0
Bình luận (0)
Gọi d là ảnh của đường thẳng 4x-3y+2=0 qua phép quay Q(O,90 độ). Tồn tại điểm M trên đường thẳng sao cho độ dài OM ngắn nhất. Hoành độ điểm M là
Trong mặt phẳng Õy cho đường tròn (C) qua phép quay tâm O(0;0) góc quay -pi/2 là đường tròn phương trình GIÚP EM VS Ạ E CẦN GẤP LẮM





