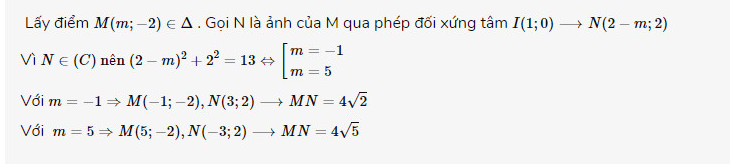trong mặt phẳng tọa độ oxy cho các điểm A(1;1) d 2x-y+5=0 và (c) (c-2)2+(y+3)2=4 tiềm ảnh cua A, d, (c) theo phép đối sứng tâm i(2;1)
Bài 4: Phép đối xứng tâm
trong mặt phẳng oxy, cho điểm m(2; 3), đường thẳng d có phương trình 3x – 2y - 6 0 và đường tròn (c) có phương trình: x 2 + y 2 - 6x + 4y - 3 0 . hãy xác định tọa độ của điểm m’, phương trình của đường thẳng d’ và đường tròn (c’) theo thứ tự là ảnh của m, d và (c) quaa) phép đối xứng qua gốc tọa độ;b) phép đối xứng qua tâm i với i (3;5).tớ đang gấp mong mn giúp với ạ TvT
Đọc tiếp
trong mặt phẳng oxy, cho điểm m(2; 3), đường thẳng d có phương trình 3x – 2y - 6 = 0 và đường tròn (c) có phương trình: x 2 + y 2 - 6x + 4y - 3 = 0 . hãy xác định tọa độ của điểm m’, phương trình của đường thẳng d’ và đường tròn (c’) theo thứ tự là ảnh của m, d và (c) qua
a) phép đối xứng qua gốc tọa độ;
b) phép đối xứng qua tâm i với i (3;5).
tớ đang gấp mong mn giúp với ạ TvT
a: Tọa độ M' là:
x'=-x=-2 và y'=-y=-3
(d'): 3x-2y+c=0
Lấy A(4;3) thuộc (d)
=>A'(-4;-3)
Thay x=-4 và y=-3 vào (d'), ta được:
c-12+6=0
=>c=6
(C): x^2+y^2-6x+4y-3=0
=>x^2-6x+9+y^2+4y+4-16=0
=>(x-3)^2+(y+2)^2=16
=>R=4; I(3;-2)
=>I'(-3;2)
=>(C'): (x+3)^2+(y-2)^2=16
b: Tọa độ M' là;
x'=2*3-2=4 và y'=2*5-3=7
(d'): 3x-2y+c=0
Lấy A(4;3) thuộc (d)
=>A'(2;7)
Thay x=2 và y=7 vào (d'), ta được:
c+6-14=0
=>c=8
R=4; I(3;-2)
=>I'(3;12)
=>(C'): (x-3)^2+(y-12)^2=16
Đúng 0
Bình luận (0)
1) Cho (C): (x-2)2 +(y+4)2 = 16 và K(1;-4). Đoy: (C)→(C1). Viết phương trình đường tròn (C1).
2) Cho A(3;-4) và B(4;2). Đd: A→B. Viết phương trình đường thẳng d.
Cho A(3;-4) và B(4;2). Đd: A →B. Viết phương trình đường thẳng d.
Đọc tiếp
Cho A(-3;0) B(-1;-7) (C): x^2+y^2-4x+8y-61=0 Tìm (C') biết T vectoBA ((C))=(C')
\(\overrightarrow{BA}=\left(-2;7\right)\)
(C') = (x - 2)2 + (y + 4)2 = 61 + 4 + 16 = 81 = 92
Gọi I (2 ; - 4) là tâm của (C) và I' (a;b) là tâm của (C')
Do \(T_{\overrightarrow{BA}}\left[\left(C\right)\right]=\left(C'\right)\)
⇒ \(T_{\overrightarrow{BA}}\left(I\right)=\left(I'\right)\)
⇒ \(\overrightarrow{II'}=\overrightarrow{BA}=\left(-2;7\right)\)
⇒ I' (0 ; 3)
Vậy phương trình đường tròn (C') là x2 + (y - 3)2 = 81
Đúng 1
Bình luận (1)
Trong mặt phẳng Oxy cho đường thẳng Δ : y + 2 = 0 và đường tròn (C) : x2 + y2 = 13. qua phép đối xứng tâm I ( 0;1) điểm M trên đường thẳng Δ biến thành điểm M thuộc (C). Độ dài nhỏ nhát của đoạn MN bằng bào nhiêu?
M thuộc Δ nên M (t ; - 2) với t là số thực
Sau khi thực hiện phép đối xứng qua tâm I (0 ; 1) thì M biến thành N (- t ; 4)
N nằm trên (C) nên t2 + 16 = 13. Vô lí, xem lại đề bài xem có sai không bạn ơi
Đúng 0
Bình luận (0)
Giải giúp e bài 2 vs ạ 
Do A đối xứng C qua I, B đối xứng D qua I
\(\Rightarrow\) CD đối xứng AB qua I và BC đối xứng AD qua I
Hay CD là ảnh của AB qua phép đối xứng tâm I, BC là ảnh của AD qua phép đối xứng tâm I
Gọi \(M\left(x;y\right)\) là 1 điểm thuộc AB \(\Rightarrow2x-y=0\) (1)
M' là ảnh của M qua phép đối xứng tâm I \(\Rightarrow M'\in DC\)
\(\left\{{}\begin{matrix}x'=2.2-x\\y=2.2-y\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=4-x'\\y=4-y'\end{matrix}\right.\) thế vào (1):
\(2\left(4-x'\right)-\left(4-y'\right)=0\Leftrightarrow-2x'+y'+4=0\Leftrightarrow2x'-y'-4=0\)
Hay pt CD có dạng: \(2x-y-4=0\)
Tương tự gọi \(N\left(x;y\right)\in AD\Rightarrow4x-3y=0\) (2)
N' là ảnh của N qua phép đối xứng tâm I
\(\Rightarrow\left\{{}\begin{matrix}x'=4-x\\y'=4-y\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=4-x'\\y=4-y'\end{matrix}\right.\) thế vào (2):
\(4\left(4-x'\right)-3\left(4-y'\right)=0\) \(\Leftrightarrow-4x'+3y'+4=0\Leftrightarrow4x'-3y'-4=0\)
Hay pt BC: \(4x-3y-4=0\)
Đúng 1
Bình luận (0)
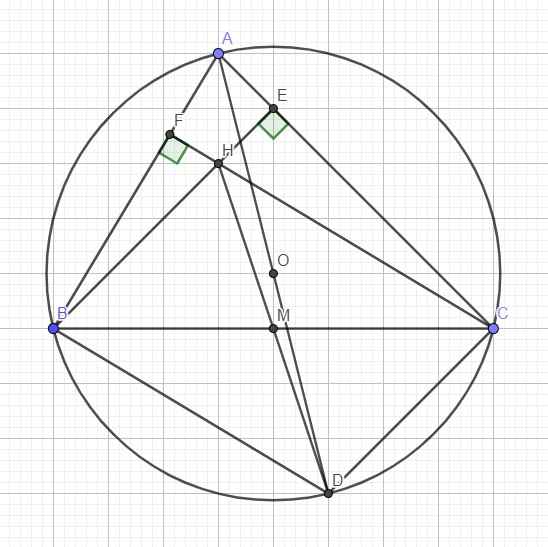
Giải giúp bài 4 với ạ

Gọi M là trung điểm BC, nối AO kéo dài cắt (O) tại D
Kẻ các đường cao BE, CF cắt nhau tại H
Ta có: \(\widehat{ABD}\) là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow BD\perp AB\)
Lại có \(CF\perp AB\) (giả thiết)
\(\Rightarrow BD||CF\)
Hoàn toàn tương tự, ta có \(CD||BE\)
\(\Rightarrow\) Tứ giác BHCD là hình bình hành (2 cặp cạnh đối song song)
\(\Rightarrow\) Hai đường chéo BC và HD cắt nhau tại trung điểm các đường
Hay M cũng là trung điểm HD
Hay H đối xứng D qua M cố định
Mà tập hợp D là đường tròn (O) cố định
\(\Rightarrow\) Tập hợp H là ảnh của (O) qua phép đối xứng tâm M cố định
Vậy trực tâm của tam giác ABC nằm trên đường tròn cố định là ảnh của (O) qua phép đối xứng tâm M
Đúng 2
Bình luận (0)
Giải giúp e bài 4 với ạ