Bài 9: Ôn tập chương Phép dời hình và phép đồng dạng trong mặt phẳng
Nội dung lý thuyết
Các phiên bản khácI. Phép biến hình
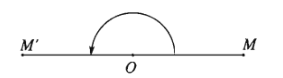
- Định nghĩa: Quy tắc đặt tương ứng mỗi điểm \(M\) của mặt phẳng với một điểm xác định duy nhất \(M'\) của mặt phẳng đó được gọi là phép biến hình trong mặt phẳng.
Nếu kí hiệu phép biến hình là \(F\) thì ta viết \(F\left(M\right)=M'\) hay \(M'=F\left(M\right)\) và gọi điểm \(M'\) là ảnh của điểm \(M\) qua phép biến hình \(F\).
Nếu \(H\) là một hình nào đó trong mặt phẳng thì ta kí hiệu \(H'=F\left(H\right)\) là tập các điểm \(M'=F\left(M\right)\), với mọi điểm \(M\) thuộc \(H\). Khi đó ta nói \(F\) biến hình \(H\) thành \(H'\), hay hình \(H'\) là ảnh của của hình \(H\) qua phép biến hình \(F\).
Phép biến hình biến mỗi điểm \(M\) thành chính nó được gọi là phép đồng nhất.
II. Phép tịnh tiến
1. Định nghĩa
Trong mặt phẳng cho vectơ \(\overrightarrow{v}\) . Phép biến hình biến mỗi điểm \(M\) thành điểm \(M'\) sao cho \(\overrightarrow{MM'}=\overrightarrow{v}\) được gọi là phép tịnh tiến theo vectơ \(\overrightarrow{v}\).
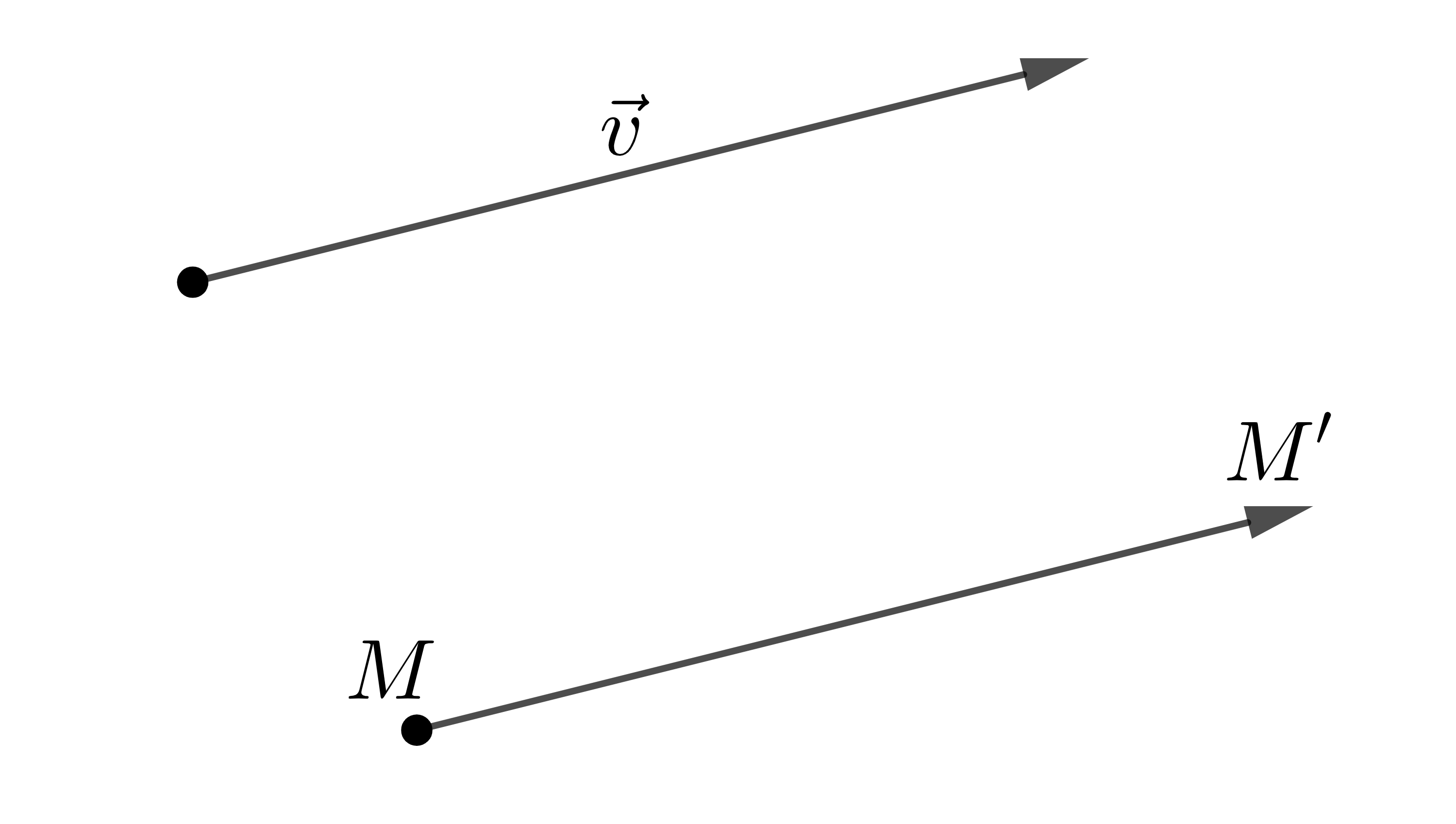
Phép tịnh tiến theo vectơ \(\overrightarrow{v}\) thường được ký hiệu là \(T_{\overrightarrow{v}}\), \(\overrightarrow{v}\) được gọi là vectơ tịnh tiến.
Như vậy:
\(T_{\overrightarrow{v}}\left(M\right)=M'\Leftrightarrow\overrightarrow{MM'}=\overrightarrow{v}\)
Phép tịnh tiến theo vectơ - không chính là phép đồng nhất.
Ta dễ dàng nhận thấy phép tịnh tiến là một phép biến hình.
2. Các tính chất của phép tịnh tiến
a) Tính chất 1:
Nếu \(T_{\overrightarrow{v}}\left(M\right)=M'\), \(T_{\overrightarrow{v}}\left(N\right)=N'\) thì \(\overrightarrow{M'N'}=\overrightarrow{MN}\) và từ đó suy ra \(M'N'=MN\).
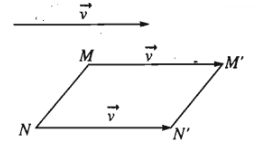
Nói cách khác, phép tịnh tiến bảo toàn khoảng cách giữa hai điểm bất kì.
b) Tính chất 2:
Phép tịnh tiến biến đường thẳng thành đường thằng song song hoặc trùng với nó, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính.
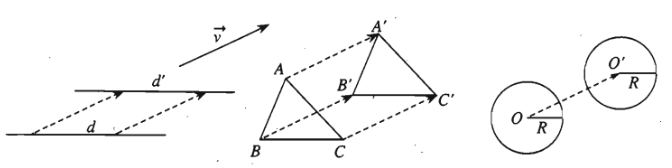
3. Biểu thức tọa độ của phép tịnh tiến
- Trong mặt phẳng \(Oxy\) cho vectơ \(\overrightarrow{v}\left(a;b\right)\) và một điểm \(M\left(x;y\right)\) . Phép tịnh tiến theo vectơ \(\overrightarrow{v}\) biến điểm \(M\) thành điểm \(M'\left(x';y'\right)\) thì \(M'\left(x';y'\right)\) có tọa độ là \(\begin{cases}x'=a+x\\y'=b+y\end{cases}\).
@62458@
III. PHÉP ĐỐI XỨNG TRỤC
1. Định nghĩa:
Cho đường thẳng \(d\). Phép biến hình biến mỗi điểm \(M\) thuộc \(d\) thành chính nó, biến mỗi điểm \(M\) không thuộc \(d\) thành điểm \(M'\) sao cho \(d\) là đường trung trực của \(MM'\) được gọi là phép đối xứng qua đường thẳng \(d\) hay là phép đối xứng trục \(d\).
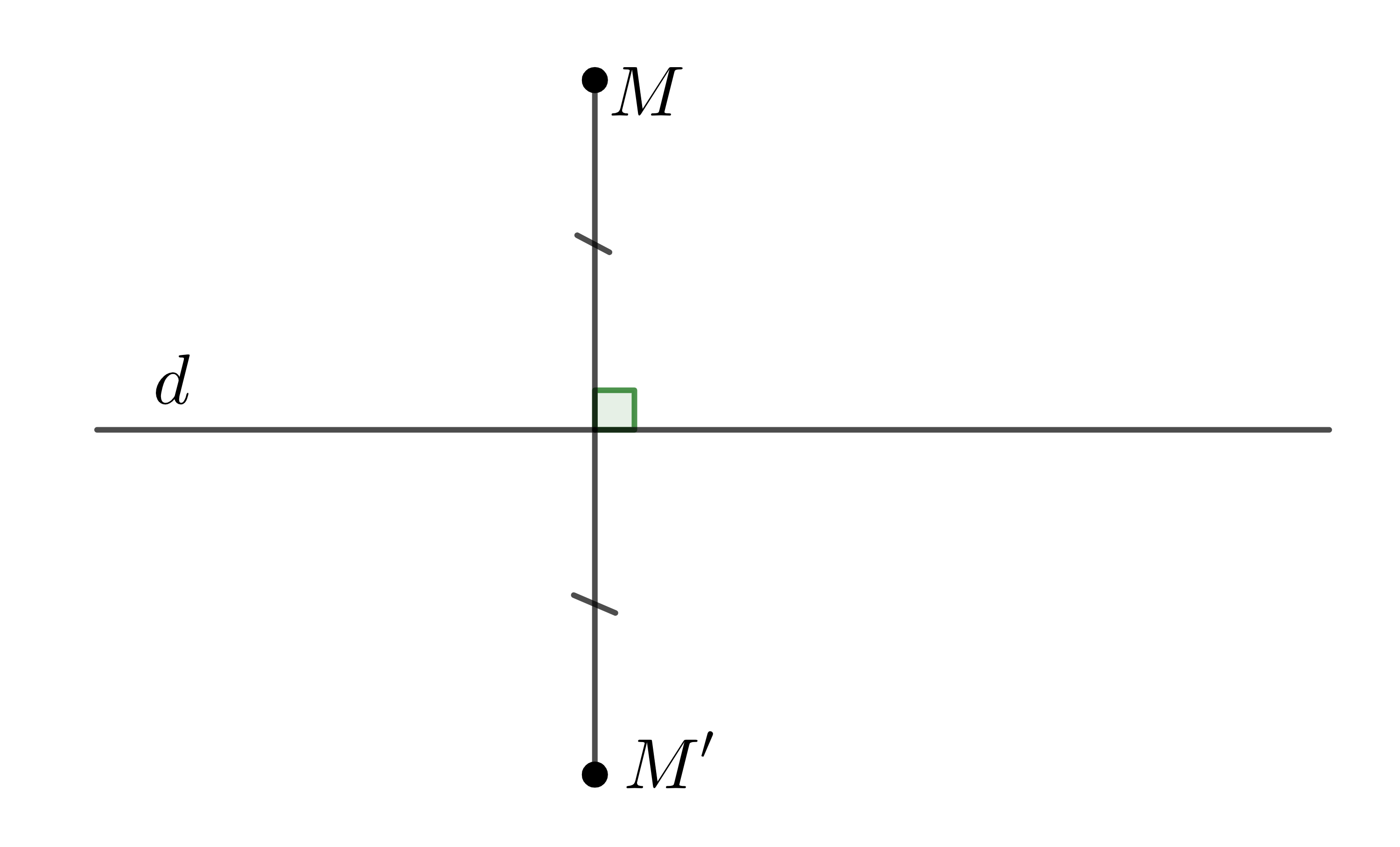
Đường thẳng \(d\) được gọi là trục của phép đối xứng hay đơn giản là trục đối xứng.
Phép đối xứng trục \(d\) thường được kí hiệu là \(Đ_d\).
Nếu hình \(H'\) là ảnh của hình \(H\) qua phép đối xứng trục \(d\) thì ta còn nói \(H\) đối xứng với \(H'\) qua \(d\), hay \(H\) và \(H'\) đối xứng nhau qua \(d\).
Nhận xét:
a) Cho đường thẳng \(d\). Với mỗi điểm \(M\), gọi \(M_0\) là hình chiếu vuông góc của \(M\) trên đường thẳng \(d\). Khi đó:
\(M'=Đ_d\left(M\right)\Leftrightarrow\overrightarrow{M_0M'}=-\overrightarrow{M_0M}\)
b) \(M'=Đ_d\left(M\right)\Leftrightarrow M=Đ_d\left(M'\right)\).
2. Biểu thức toạ độ
Chọn hệ toạ độ \(Oxy\) sao cho \(Ox\) trùng với đường thẳng \(d\). Với mỗi điểm \(M\left(x;y\right)\), gọi \(M'=Đ_d\left(M\right)=\left(x';y'\right)\) thì \(\begin{cases}x'=x\\y'=-y\end{cases}\) . Biểu thức này được goị là biểu thức toạ độ của phép đối xứng qua trục \(Ox\).
. Biểu thức này được goị là biểu thức toạ độ của phép đối xứng qua trục \(Ox\).
Chọn hệ toạ độ \(Oxy\) sao cho \(Oy\) trùng với đường thẳng \(d\). Với mỗi điểm \(M\left(x;y\right)\), gọi \(M'=Đ_d\left(M\right)=\left(x';y'\right)\) thì \(\left\{{}\begin{matrix}x'=-x\\y'=y\end{matrix}\right.\). Biểu thức này được goị là biểu thức toạ độ của phép đối xứng qua trục \(Oy\).
3. Tính chất
a) Tính chất 1: Phép đối xứng trục bảo toàn khoảng cách giữa hai điểm bất kỳ .
b) Tính chất 2: Phép đối xứng trục biến đường thẳng thành đường thẳng, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính.

4. Trục đối xứng của một hình
Định nghĩa:
IV. PHÉP ĐỐI XỨNG TÂM
1. Định nghĩa
Cho điểm \(I\). Phép biến hình biến điểm \(I\) thành chính nó, biến mỗi điểm \(M\) khác \(I\) thành \(M'\) sao cho \(I\) là trung điểm của đoạn thẳng \(MM'\) được gọi là phép đối xứng tâm \(I\).
Điểm \(I\) được gọi là tâm đối xứng.

Phép đối xứng tâm \(I\) thường được kí hiệu là \(Đ_I\).
Từ định nghĩa trên ta suy ra
\(M'=Đ_I\left(M\right)\Leftrightarrow\overrightarrow{IM'}=-\overrightarrow{IM}\)
Nhận xét: \(M'=Đ_I\left(M\right)\Leftrightarrow M=Đ_I\left(M'\right)\)
2. Biểu thức toạ độ của phép đối xứng qua gốc toạ độ
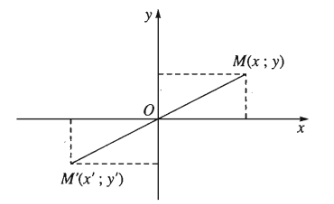
Trong hệ toạ độ \(Oxy\) cho điểm \(M\left(x;y\right)\), \(M'=Đ_I\left(M\right)=\left(x';y'\right)\) , khi đó \(\left\{{}\begin{matrix}x'=-x\\y'=-y\end{matrix}\right.\).
Biểu thức này được gọi là biểu thức toạ độ của phép đối xứng qua gốc toạ độ.
3. Tính chất
a) Tính chất 1:
Nếu \(Đ_I\left(M\right)=M'\) và \(Đ_I\left(N\right)=N'\) thì \(\overrightarrow{M'N'}=-\overrightarrow{MN}\), từ đó suy ra \(M'N'=MN\).
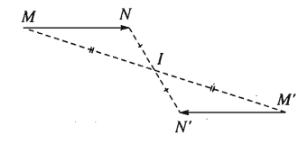
Nói cách khác, phép đối xứng tâm bảo toàn khoảng cách giữa hai điểm bất kì.
b) Tính chất 2:
Phép đối xứng tâm biến đường thẳng thành đường thẳng song song hoặc trùng với nó, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính.
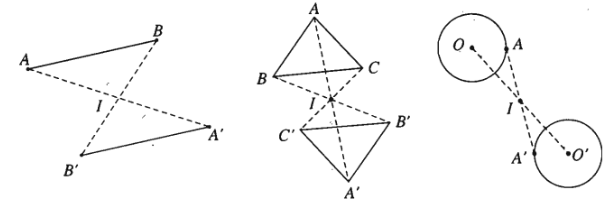
4. Tâm đối xứng của một hình
Định nghĩa: Điểm \(I\) được gọi là tâm đối xứng của hình \(H\) nếu phép đối xứng tâm \(I\) biến \(H\) thành chính nó.
Khi đó ta nói \(H\) là hình có tâm đối xứng.
V. PHÉP QUAY
1. Định nghĩa
Cho điểm \(O\) và góc lượng giác \(\alpha\). Phép biến hình biến \(O\) thành chính nó, biễn mỗi điểm \(M\) khác \(O\) thành điểm \(M'\) sao cho \(OM'=OM\) và góc lượng giác \(\left(OM;OM'\right)\) bằng \(\alpha\) được gọi là phép quay tâm \(O\) góc \(\alpha\).
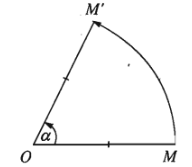
Điểm \(O\) được gọi là tâm quay còn \(\alpha\) được gọi là góc quay của phép quay đó.
Kí hiệu: Phép quay tâm \(O\) góc \(\alpha\) được kí hiệu là \(Q_{\left(O,\alpha\right)}\).
Nhận xét:
1) Chiều dương của phép quay là chiều dương của đường tròn lượng giác nghĩa là chiều ngược với chiều quay của kim đồng hồ.

2) Với \(k\) là số nguyên ta luôn có:
Phép quay \(Q_{\left(O;2k\pi\right)}\) là phép đồng nhất.
Phép quay \(Q_{\left(O;\left(2k+1\right)\pi\right)}\) là phép đối xứng tâm \(O\).
2. Tính chất
a) Tính chất 1: Phép quay bảo toàn khoảng cách giữa hai điểm bất kì.
b) Tính chất 2: Phép quay biến đường thẳng thành đường thẳng, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính.
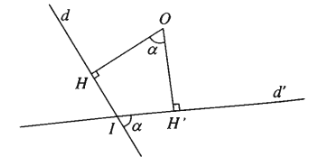
Nhận xét: Phép quay góc \(\alpha\) với \(0< \alpha< \pi\), biến đường thẳng \(d\) thành đường thẳng \(d'\) sao cho góc giữa \(d\) và \(d'\) bằng \(\alpha\) (nếu \(0< \alpha< \dfrac{\pi}{2}\)), hoặc bằng \(\pi-\alpha\) (nếu \(\dfrac{\pi}{2}< a< \pi\)).
VI. KHÁI NIỆM VỀ PHÉP DỜI HÌNH VÀ HAI HÌNH BẰNG NHAU
1. Khái niệm về phép dời hình
Định nghĩa: Phép dời hình là phép biến hình bảo toàn khoảng cách giữa hai điểm bất kì.
Nếu phép dời hình \(F\) biến các điểm \(M,N\) lần lượt thành các điểm \(M',N'\) thì \(MN=M'N'\).
Nhận xét:
- Các phép đồng nhất, phép tịnh tiến, phép đối xứng trục, phép đối xứng tâm và phép quay đều là các phép dời hình.
- Phép biến hình có được bằng cách thực hiện liên tiếp các phép dời hình cũng là một phép dời hình.
2. Tính chất
Phép dời hình:
1) Biến ba điểm thằng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm ;
2) Biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thành đoạn bằng nó ;
3) Biến tam giác thành tam giác bằng nó, biến góc thành góc bằng nó ;
4) Biến đường tròn thành đường tròn có cùng bán kính.
Chú ý:
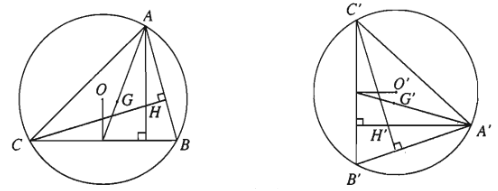
a) Nếu một phép dời hình biến tam giác \(ABC\) thành tam giác \(A'B'C'\) thì nó cũng biến trọng tâm, trực tâm, tâm các đường trọn nội tiếp, ngoại tiếp.. của tam giác \(ABC\) tương ứng thành trọng tâm, trực tâm, tâm các đường trọng nội tiếp, ngoại tiếp... của tam giác \(A'B'C'\).
b) Phép dời hình biến đa giác \(n\) cạnh thành đa giác \(n\) cạnh, biến đỉnh thành đỉnh, biến cạnh thành cạnh.
3. Khái niệm hai hình bằng nhau
Định nghĩa: Hai hình được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia.
VII. PHÉP VỊ TỰ
1. Định nghĩa
Cho điểm \(O\) và số \(k\ne0\). Phép biến hình biến mỗi điểm \(M\) thành điểm \(M'\) sao cho \(\overrightarrow{OM'}=k\overrightarrow{OM}\) được gọi là phép vị tự tâm \(O\), tỉ số \(k\).

Phép vị tự tâm \(O\), tỉ số \(k\) thường được kí hiệu là \(V_{\left(O;k\right)}\).
Nhận xét:
1) Phép vị tự biến tâm vị tự thành chính nó.
2) Khi \(k=1\), phép vị tự là phép đồng nhất.
3) Khi \(k=-1\), phép vị tự là phép đối xứng qua tâm vị tự.
4) \(M'=V_{\left(O;k\right)}\left(M\right)\Leftrightarrow M=V_{\left(O;\dfrac{1}{k}\right)}\left(M'\right)\).
2. Tính chất
a) Tính chất 1: Nếu phép vị tự tỉ số \(k\) biến hai điểm \(M,N\) tuỳ ý theo thứ tự thành \(M',N'\) thì \(\overrightarrow{M'N'}=k\overrightarrow{MN}\) và \(M'N'=\left|k\right|.MN\).
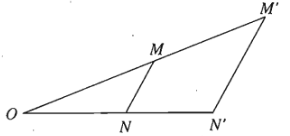
2) Tính chất 2:
Phép vị tự tỉ số \(k\):
a) Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm ấy.
b) Biến đường thẳng thành đường thẳng song song hoặc trùng với nó, biến tia thành tia, biến đoạn thẳng thành đoạn thằng.
c) Biến tam giác thành tam giác đồng dạng với nó, biến góc thành góc bằng nó.
d) Biến đường tròn bán kính \(R\) thành đường tròn bán kinh \(\left|k\right|R\).

3. Tâm vị tự của hai đường tròn
Định lí: Với hai đường tròn bất kì luôn có một phép vị tự biến đường tròn này thành đường tròn kia.
Tâm của phép vị tự đó được gọi là tâm vị tự của hai đường tròn.
Cách tìm tâm vị tự của hai đường tròn:
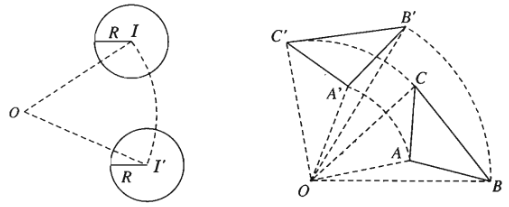
Cho hai đường tròn \(\left(I;R\right)\) và \(\left(I';R'\right)\). Có ba trường hợp xảy ra:
+) Trường hợp \(I\) trùng với \(I'\):
Khi đó \(V_{\left(I;\dfrac{R'}{R}\right)}\) và \(V_{\left(I;-\dfrac{R'}{R}\right)}\) biến đường tròn \(\left(I;R\right)\) thành đường tròn \(\left(I';R'\right)\).

+) Trường hợp \(I\) khác \(I'\) và \(R\ne R'\):
Lấy \(M\in\left(I;R\right)\), đường thẳng qua \(I'\) song song với \(IM\) cắt \(\left(I';R'\right)\) tại \(M'\) và \(M''\). Giả sử \(M,M'\) nằm cùng phía đối với đường thẳng \(II'\) còn \(M,M''\) nằm khác phía đối với đường thẳng \(II'\). Giả sử đường thẳng \(MM'\) cắt đường thẳng \(II'\) tại \(O\) nằm ngoài đoạn thẳng \(II'\) , còn đường thẳng \(MM''\) cắt đường thẳng \(II'\) tại \(O_1\) nằm trong đoạn thẳng \(II'\).
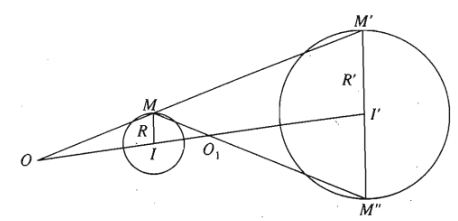
Khi đó \(V_{\left(O;k\right)}\) với \(k=\dfrac{R'}{R}\) và \(V_{\left(O_1;k_1\right)}\) với \(k_1=-\dfrac{R'}{R}\) biến đường tròn \(\left(I;R\right)\) thành đường tròn \(\left(I';R'\right)\).
Ta gọi \(O\) là tâm vị tự ngoài còn \(O_1\) là tâm vị tự trong của hai đường tròn đó.
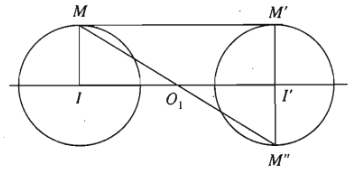
+) Trường hợp \(I\) khác \(I'\) và \(R'=R\):
Khi đó \(MM'\) // \(II'\) nên chỉ có \(V_{\left(O_1;k_1\right)}\) với \(k_1=-\dfrac{R'}{R}=-1\) biến đường tròn \(\left(I;R\right)\) thành đường tròn \(\left(I';R'\right)\).
@62465@
VIII. PHÉP ĐỒNG DẠNG
1. Định nghĩa
Phép biến hình \(F\) được gọi là phép đồng dạng tỉ số \(k\) (\(k>0\)), nếu với hai điểm \(M,N\) bất kì và ảnh \(M',N'\) tương ứng của chúng ta luôn có \(M'N'=k.MN\).
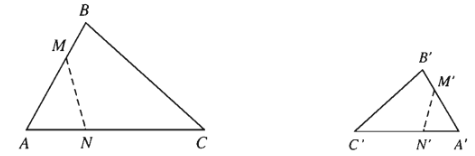
Nhận xét:
1) Phép dời hình là phép đồng dạng tỉ số 1.
2) Phép vị tự tỉ số \(k\) là phép đồng dạng tỉ số \(\left|k\right|\).
3) Nếu thực hiện liên tiếp phép đồng dạng tỉ số \(k\) và phép đồng dạng tỉ số \(p\) ta được phép đồng dạng tỉ số \(kp\).
2. Tính chất
Phép đồng dạng tỉ số \(k\):
a) Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm ấy.
b) Biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng.
c) Biến tam giác thành tam giác đồng dạng với nó, biến góc thành góc bằng nó.
d) Biến đường tròn bán kính \(R\) thành đường tròn bán kinh \(kR\).
Chú ý:
a) Nếu một phép đồng dạng biến tam giác \(ABC\) thành tam giác \(A'B'C'\) thì nó cũng biến trọng tâm, trực tâm, tâm các đường tròn nội tiếp, ngoại tiếp của tam giác \(ABC\) tương ứng thành trọng tâm, trực tâm, tâm các đường tròn nội tiếp, ngoại tiếp của tam giác \(A'B'C'\).
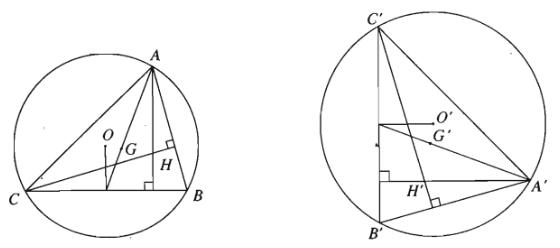
b) Phép đồng dạng biến đa giác \(n\) cạnh thành đa giác \(n\) cạnh, biến đỉnh thành đỉnh, biến cạnh thành cạnh.
3. Hình đồng dạng
Chúng ta đa biết phép đồng dạng biến một tam giác thành một tam giác đồng dạng với nó. Người ta cũng chứng minh được rằng cho hai tam giác đồng dạng với nhau thì luôn có một phép đồng dạng biến tam giác này thành tam giác kia. Vậy hai tam giác đồng dạng với nhau khi và chỉ khi có một phép đồng dạng biến tam giác này thành tam giác kia.
Từ đó ta có định nghĩa:
Hai hình được gọi là đồng dạng với nhau nếu có một phép đồng dạng biến hình này thành hình kia.
@2135260@