Bài 3: Phép đối xứng trục
Nội dung lý thuyết
Các phiên bản khácI. ĐỊNH NGHĨA
Cho đường thẳng \(d\). Phép biến hình biến mỗi điểm \(M\) thuộc \(d\) thành chính nó, biến mỗi điểm \(M\) không thuộc \(d\) thành điểm \(M'\) sao cho \(d\) là đường trung trực của \(MM'\) được gọi là phép đối xứng qua đường thẳng \(d\) hay là phép đối xứng trục \(d\).
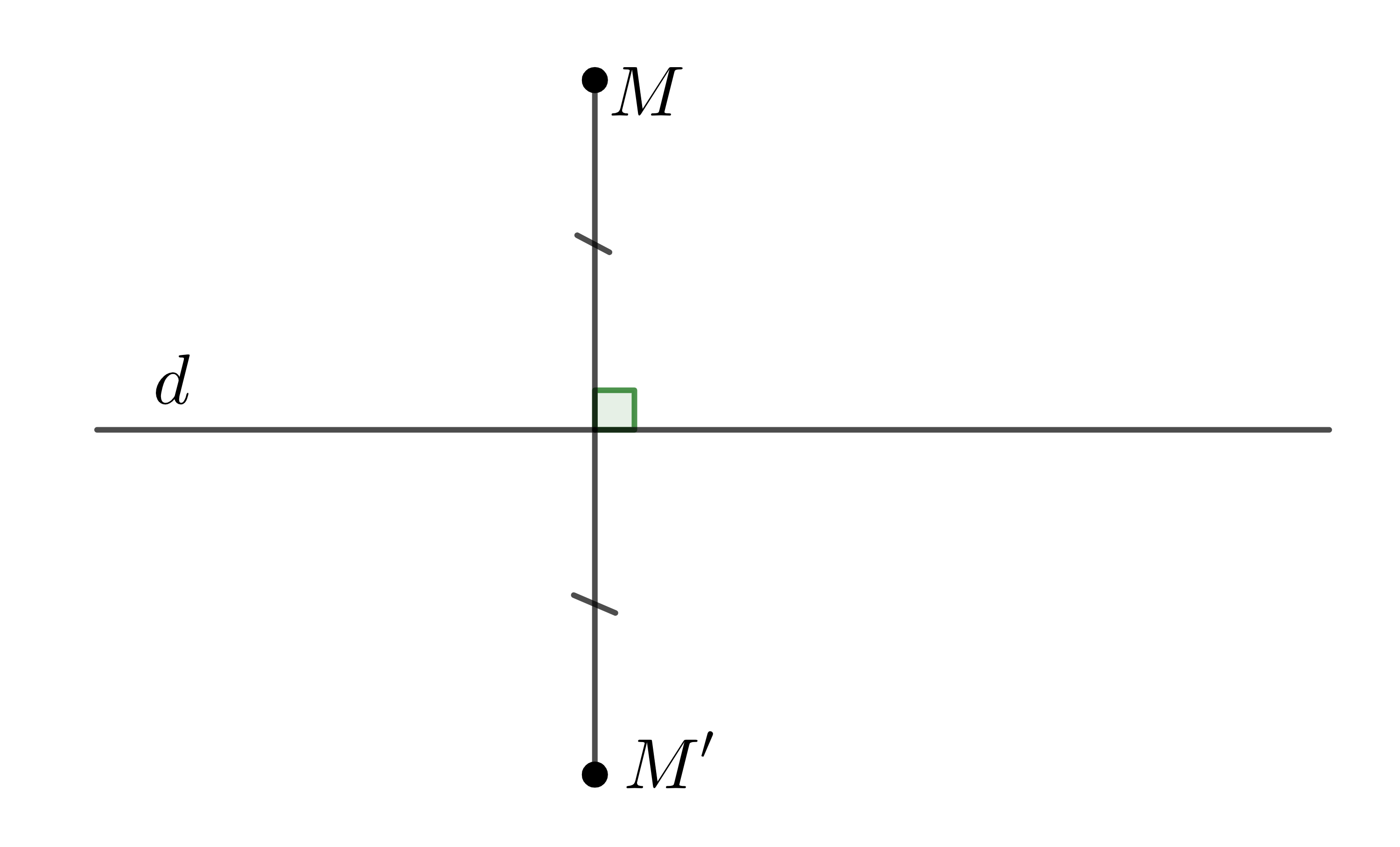
Đường thẳng \(d\) được gọi là trục của phép đối xứng hay đơn giản là trục đối xứng.
Phép đối xứng trục \(d\) thường được kí hiệu là \(Đ_d\).
Nếu hình \(H'\) là ảnh của hình \(H\) qua phép đối xứng trục \(d\) thì ta còn nói \(H\) đối xứng với \(H'\) qua \(d\), hay \(H\) và \(H'\) đối xứng nhau qua \(d\).
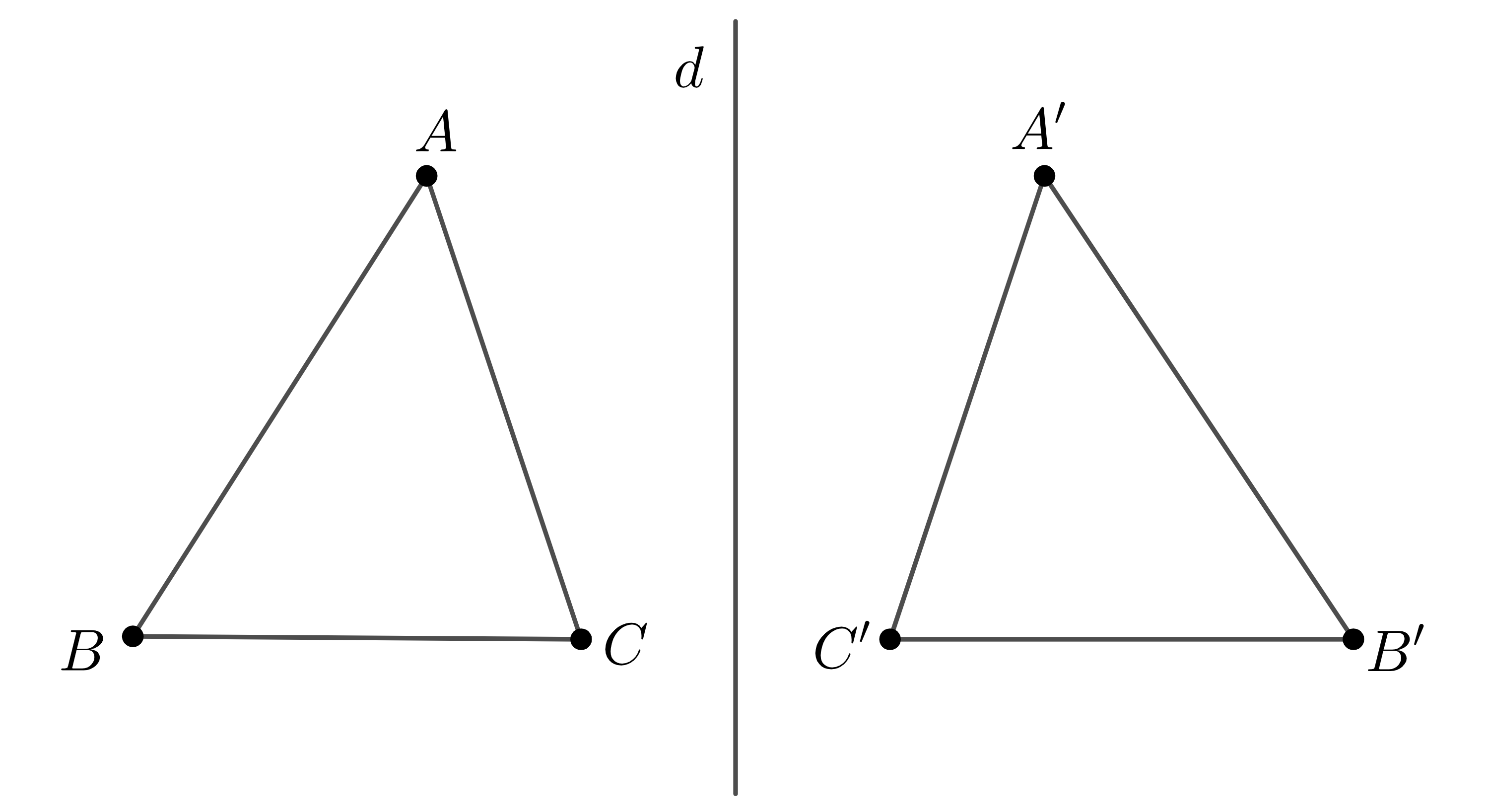
Ví dụ 1: Trong hình vẽ dưới đây, các điểm \(A',B',C'\) lần lượt là ảnh của các điểm \(A,B,C\) qua phép đối xứng trục \(d\) và ngược lại. Ta cũng nói ta giác \(ABC\) và tam giác \(A'B'C'\) đối xứng nhau qua \(d\).
Nhận xét:
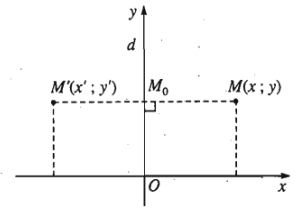
a) Cho đường thẳng \(d\). Với mỗi điểm \(M\), gọi \(M_0\) là hình chiếu vuông góc của \(M\) trên đường thẳng \(d\). Khi đó:
\(M'=Đ_d\left(M\right)\Leftrightarrow\overrightarrow{M_0M'}=-\overrightarrow{M_0M}\)
b) \(M'=Đ_d\left(M\right)\Leftrightarrow M=Đ_d\left(M'\right)\).
Ví dụ 2: Cho hình thoi \(ABCD\). Tìm ảnh của các điểm \(A,B,C,D\) qua phép đối xứng trục \(AC\).
Giải:
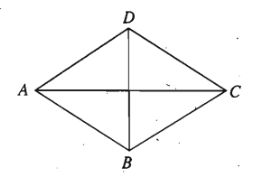
Do \(A,C\in AC\) nên ảnh của hai điểm \(A\) và \(C\) qua phép đối xứng trục \(AC\) là chính nó.
Theo tính chất của hình thoi, \(AC\perp BD\) tại trung điểm mỗi đường nên \(AC\) là đường trung trực của đoạn \(BD\)
\(\Rightarrow\) \(B\) và \(D\) đối xứng nhau qua \(AC\)
Nên ảnh của \(B\) và \(D\) qua phép đối xứng trục \(AC\) lần lượt là \(D\) và \(B\).
@50935@
II. BIỂU THỨC TOẠ ĐỘ
1) Chọn hệ toạ độ \(Oxy\) sao cho \(Ox\) trùng với đường thẳng \(d\). Với mỗi điểm \(M\left(x;y\right)\), gọi \(M'=Đ_d\left(M\right)=\left(x';y'\right)\) thì \(\begin{cases}x'=x\\y'=-y\end{cases}\) . Biểu thức này được goị là biểu thức toạ độ của phép đối xứng qua trục \(Ox\).
. Biểu thức này được goị là biểu thức toạ độ của phép đối xứng qua trục \(Ox\).
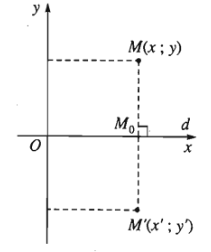
Ví dụ: +) Ảnh của điểm \(A\left(1;2\right)\) qua phép đối xứng trục \(Ox\) là điểm \(A'\left(1;-2\right)\) ;
+) Ảnh của điểm \(B\left(0;-5\right)\) qua phép đối xứng trục \(Ox\) là điểm \(B\left(0;5\right)\) ; ...
2) Chọn hệ toạ độ \(Oxy\) sao cho \(Oy\) trùng với đường thẳng \(d\). Với mỗi điểm \(M\left(x;y\right)\), gọi \(M'=Đ_d\left(M\right)=\left(x';y'\right)\) thì \(\left\{{}\begin{matrix}x'=-x\\y'=y\end{matrix}\right.\). Biểu thức này được goị là biểu thức toạ độ của phép đối xứng qua trục \(Oy\).
Ví dụ: +) Ảnh của điểm \(A\left(1;2\right)\) qua phép đối xứng trục \(Oy\) là điểm \(A'\left(-1;2\right)\) ;
+) Ảnh của điểm \(B\left(5;0\right)\) qua phép đối xứng trục \(Oy\) là điểm \(B'\left(-5;0\right)\) ; ...
Ví dụ 3: Trong mặt phẳng \(Oxy\) cho đường thằng \(\left(d\right):3x-y+2=0\). Viết phương trình đường thẳng \(\left(d'\right)\) là ảnh của \(\left(d\right)\) qua phép đối xứng trục \(Oy\) .
Giải:
Gọi \(M\left(x;y\right)\) là một điểm tuỳ ý nằm trên đường thẳng \(\left(d\right)\), suy ra \(3x-y+2=0\)
Giả sử \(M'\left(x';y'\right)=Đ_{Oy}\left(M\right)\) \(\Rightarrow\left\{{}\begin{matrix}x'=-x\\y'=y\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=-x'\\y=y'\end{matrix}\right.\)
Khi đó ta có thể viết lại \(M\left(-x';y'\right)\in\left(d\right)\), suy ra \(3\left(-x'\right)-\left(y'\right)+2=0\) hay \(3x'+y'-2=0\)
Như vậy điểm \(M'\in\left(d'\right):3x+y-2=0\)
Vậy phương trình đường thẳng \(\left(d'\right)\) là ảnh của \(\left(d\right)\) qua phép đối xứng trục \(Oy\) là \(3x+y-2=0\).
@50896@
III. TÍNH CHẤT
a) Tính chất 1:
Phép đối xứng trục bảo toàn khoảng cách giữa hai điểm bất kỳ .
b) Tính chất 2:
Phép đối xứng trục biến đường thẳng thành đường thẳng, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính.

IV. TRỤC ĐỐI XỨNG CỦA MỘT HÌNH
Định nghĩa:
Đường thẳng \(d\) được gọi là trục đối xứng của hình \(H\) nếu phép đối xứng qua \(d\) biến hình \(H\) thành chính nó .
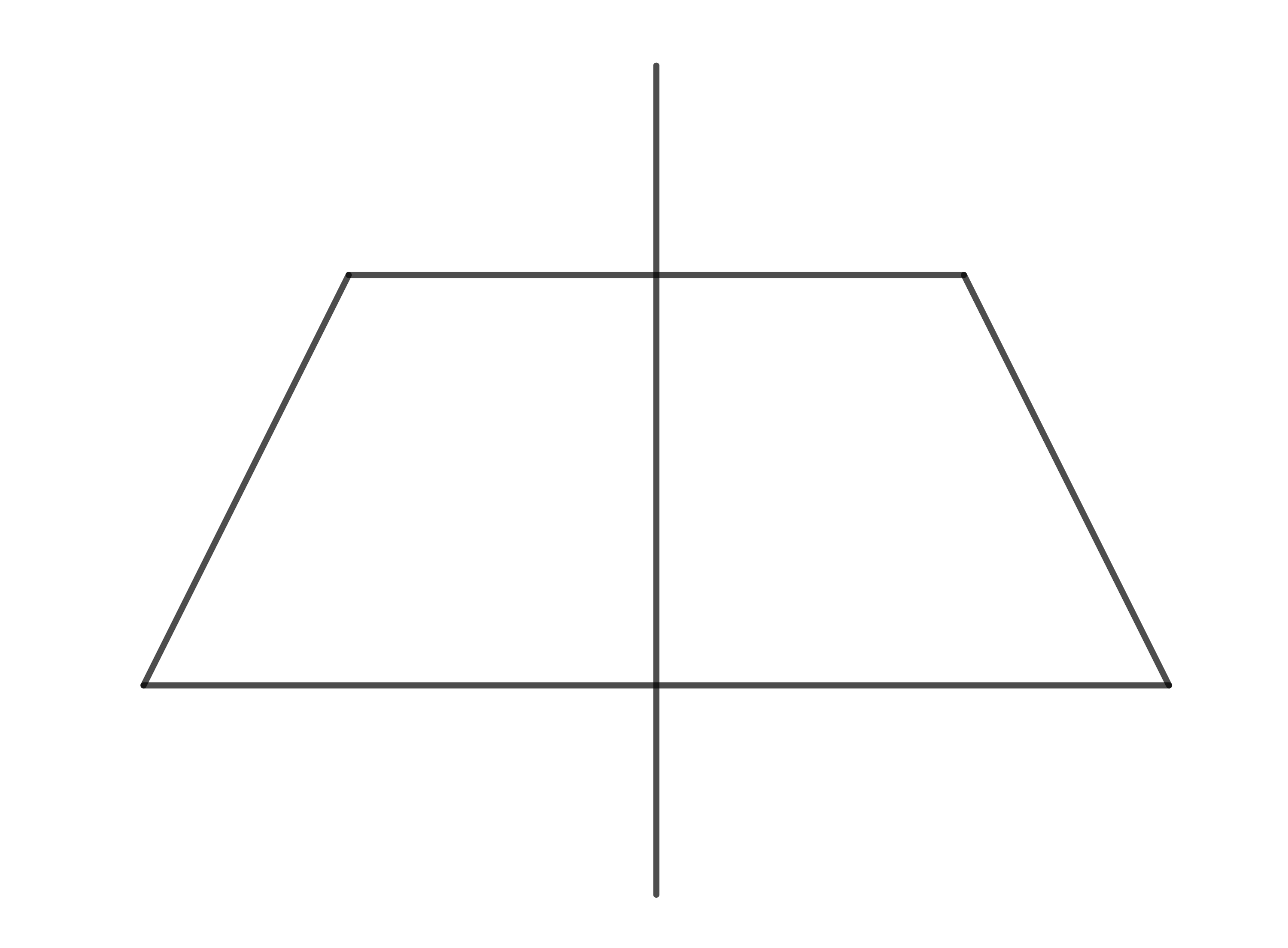
Ví dụ: Hình thang cân có đối xứng trục là đường thẳng nối trung điểm của hai cạnh đáy.
@25377@