Giúp mình với 😢
Bài 5: Khảo sát sự biến thiên và vẽ đồ thị hàm số
Cau 8: A
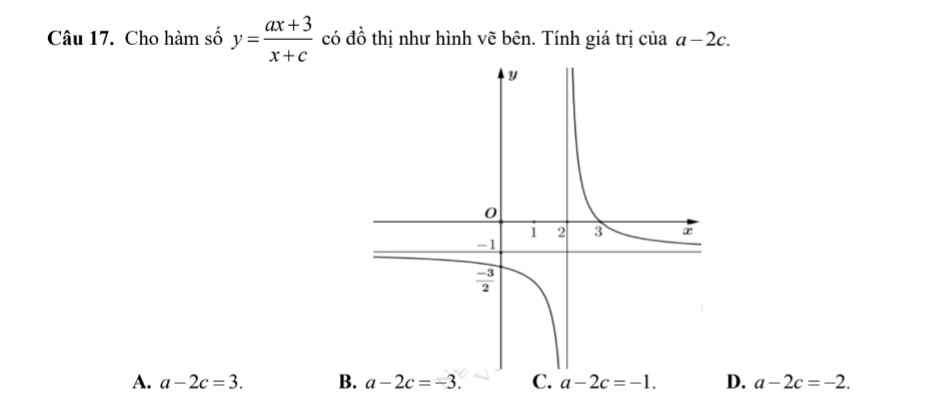
Câu 17: B
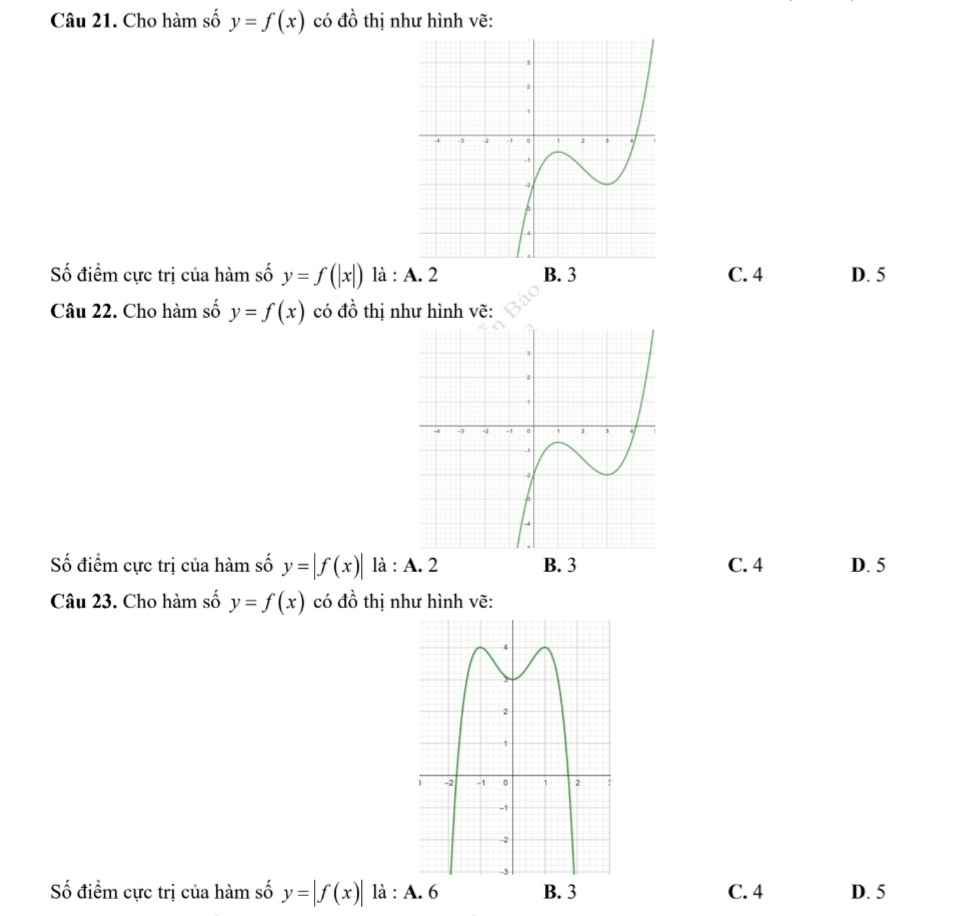
Cau 21: C
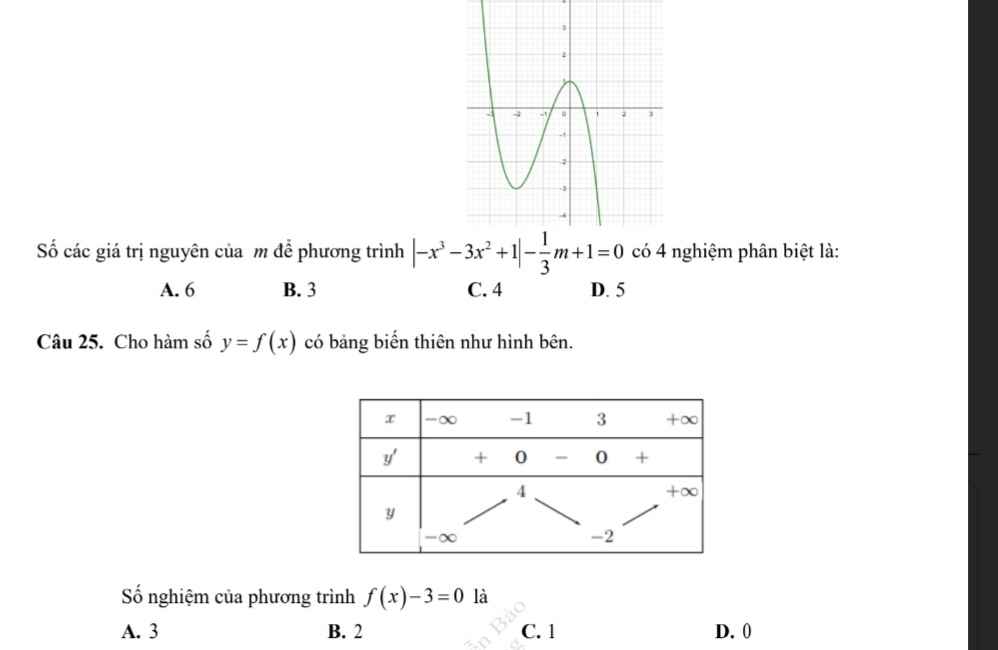
Câu 25: B
Câu 23: A
Đúng 0
Bình luận (0)
Bài 1 a) Khảo sát và vẽ đồ thị hàm số y=x³-2x²+x (C) b) từ đồ thị (C) suy ra đồ thị các hàm số sau: y=|x³-2x²+x|, y=|x|³ -2x²+|x| Bài 2: Khảo sát và vẽ đồ thị hàm số y=x⁴-2x²-3 (C). Từ đồ thị (C) suy ra đồ thị hàm số y=|y=x⁴-2x²-3|
Cho hàm số \(y=-x^3+3x-2\) (C)
a) Khảo sát và vẽ đồ thị hàm số
b) Tìm m để phương trình: \(x^3-3x+2m+1=0\) có 3 nghiệm phân biệt
c) Viết phương trình tiếp tuyến với (C) tại điểm có hoành độ \(x=0\)
Khảo sát sự biến thiên và vẽ đồ thị hàm số:
a) y= x4+2x2-3
b) y= -x4-4x-1
Khảo sát sự biến thiên và vẽ đồ thị hầm số:
a) y= x4+2x2-3
b) y= -x4-4x-1
Giải giúp mình câu 2,3,4 với
1.tìm m để hs y=\(\left(m-1\right)x^4-2\left(m-3\right)x^2+1\) không có cực đại
2. có bn số nguyên m để hs y=\(x^3+mx-\dfrac{1}{5x^2}\) đồng biến trên \(\left(0;+\infty\right)\)
3. có bn số nguyên m để hs y=\(\dfrac{mx-4}{x-m}\) tăng trên \(\left(0;+\infty\right)\)
1. có bn số nguyên m để y=\(\dfrac{mx+3}{3x+m}\) giảm trên \(\left(0;+\infty\right)\)
2. tìm m đẻ hs y=\(-x^3-6x^2+\left(4m-9\right)x+4\) giảm trên \(\left(-\infty;-1\right)\)
3. tìm m để y=\(x^3-mx^2+x+1\) tăng trên \(\left(0;+\infty\right)\)
1, y' = \(\dfrac{m^2-9}{\left(3x-m\right)^2}\)
ycbt <=> \(\left\{{}\begin{matrix}m^2-9< 0\\\dfrac{m}{-3}\ne x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3< m< 3\\m\ge0\end{matrix}\right.\)
\(\Leftrightarrow0\le m\le3\)
Đúng 1
Bình luận (5)
tìm m để \(x^3+3x^2+\left(1-m\right)x+1\ge0\) ( mọi x >=0)
tìm m để pt có 2ng phân biệt \(\sqrt{x^2+mx+2}=2x+1\)
a.
\(\Leftrightarrow x^3+3x^2+x+1\ge mx\) ; \(\forall x\ge0\) (1)
- Với \(x=0\) thỏa mãn
- Với \(x>0\)
(1) \(\Leftrightarrow x^2+3x+1+\dfrac{1}{x}\ge m\)
\(\Leftrightarrow m\le\min\limits_{x>0}\left(x^2+3x+1+\dfrac{1}{x}\right)\)
Xét \(f\left(x\right)=x^2+3x+1+\dfrac{1}{x}\) với \(x>0\)
\(f'\left(x\right)=2x+3-\dfrac{1}{x^2}=0\Leftrightarrow\dfrac{\left(2x-1\right)\left(x+1\right)^2}{x^2}=0\Rightarrow x=\dfrac{1}{2}\)
Từ BBT ta thấy \(f\left(x\right)_{min}=f\left(\dfrac{1}{2}\right)=\dfrac{19}{4}\)
\(\Rightarrow m\le\dfrac{19}{4}\)
Đúng 3
Bình luận (0)
b.
Bài toán thỏa mãn khi:
\(x^2+mx+2=\left(2x+1\right)^2\Leftrightarrow3x^2-\left(m-4\right)x-1=0\) (1) có 2 nghiệm pb thỏa mãn \(-\dfrac{1}{2}\le x_1< x_2\) (2)
Do \(ac=-3< 0\) nên (1) luôn có 2 nghiệm pb
Để 2 nghiệm của (1) thỏa mãn (2) thì:
\(\left\{{}\begin{matrix}\left(x_1+\dfrac{1}{2}\right)\left(x_2+\dfrac{1}{2}\right)\ge0\\\dfrac{x_1+x_2}{2}>-\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1x_2+\dfrac{1}{2}\left(x_1+x_2\right)+\dfrac{1}{4}\ge0\\x_1+x_2>-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{1}{3}+\dfrac{m-4}{6}+\dfrac{1}{4}\ge0\\\dfrac{m-4}{3}>-1\end{matrix}\right.\) \(\Rightarrow m\ge\dfrac{9}{2}\)
Đúng 1
Bình luận (0)
cho hs y=\(x^3+\left(m+3\right)x^2-2-m=0\) (1)
m? để (1) cắt Ox tại 3 điểm pb
Pt hoành độ giao điểm:
\(x^3+\left(m+3\right)x^2-2-m=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+\left(m+2\right)x-m-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x^2+\left(m+2\right)x-m-2=0\left(1\right)\end{matrix}\right.\)
Đồ thị hàm số cắt Ox tại 3 điểm pb khi và chỉ khi (1) có 2 nghiệm pb khác -1
\(\Leftrightarrow\left\{{}\begin{matrix}a-b+c=1-\left(m+2\right)-m-2\ne0\\\Delta=\left(m+2\right)^2+4\left(m+2\right)>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-2m-3\ne0\\m^2+8m+12>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m\ne-\dfrac{3}{2}\\\left[{}\begin{matrix}m>-2\\m< -6\end{matrix}\right.\end{matrix}\right.\)
Đúng 0
Bình luận (0)



