1,
\(f\left(x\right)=x-sin2x+2\)
\(f'\left(x\right)=1-2cos2x=0\Rightarrow cos2x=\dfrac{1}{2}\)
\(\Rightarrow2x=\dfrac{\pi}{3}+k2\pi\)
\(\Rightarrow x=\pm\dfrac{\pi}{6}+k\pi\)
\(x\in\left(-2\pi;2\pi\right)\Rightarrow x=\left\{-\dfrac{11\pi}{6};-\dfrac{7\pi}{6};-\dfrac{5\pi}{6};-\dfrac{\pi}{6};\dfrac{\pi}{6};\dfrac{5\pi}{6};\dfrac{7\pi}{6};\dfrac{11\pi}{6}\right\}\)
BBT:
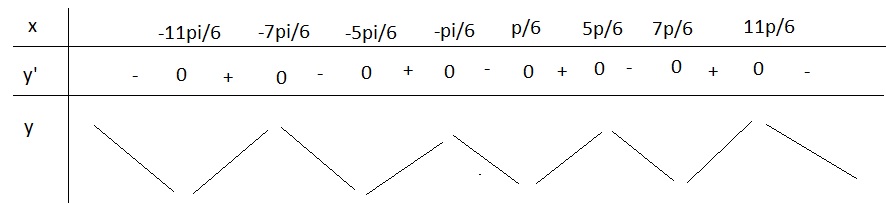
Từ BBT ta thấy trên khoảng đã cho:
Hàm đạt cực đại tại các điểm \(x=\left\{-\dfrac{7\pi}{6};-\dfrac{\pi}{6};\dfrac{5\pi}{6};\dfrac{11\pi}{6}\right\}\)
Hàm đạt cực tiểu tại các điểm \(x=\left\{-\dfrac{11\pi}{6};-\dfrac{5\pi}{6};\dfrac{\pi}{6};\dfrac{7\pi}{6}\right\}\)
2.
\(\lim\limits_{x\rightarrow\pm\infty}\dfrac{x^2+2x-3}{x^2-4x+3}=\lim\limits_{x\rightarrow\pm\infty}\dfrac{1+\dfrac{2}{x}-\dfrac{3}{x^2}}{1-\dfrac{4}{x}+\dfrac{3}{x^2}}=1\)
\(\Rightarrow y=1\) là 1 TCN của đồ thị hàm số
\(\lim\limits_{x\rightarrow1}\dfrac{x^2+2x-3}{x^2-4x+3}=\lim\limits_{x\rightarrow1}\dfrac{\left(x-1\right)\left(x+3\right)}{\left(x-1\right)\left(x-3\right)}=\lim\limits_{x\rightarrow1}\dfrac{x+3}{x-3}=-2\)
\(\Rightarrow x=1\) không là tiệm cận
\(\lim\limits_{x\rightarrow3^+}\dfrac{x^2+2x-3}{x^2-4x+3}=\lim\limits_{x\rightarrow3^+}\dfrac{\left(x-1\right)\left(x+3\right)}{\left(x-1\right)\left(x-3\right)}=\lim\limits_{x\rightarrow3^+}\dfrac{x+3}{x-3}=+\infty\)
\(\Rightarrow x=3\) là TCĐ của ĐTHS
Vậy ĐTHS đã cho có 1 TCĐ là \(x=3\) và 1 TCN \(y=1\)
3.
Pt hoành độ giao điểm:
\(\left(x+1\right)\left(x^2+2mx+m+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\f\left(x\right)=x^2+2mx+m+2=0\left(1\right)\end{matrix}\right.\)
ĐTHS cắt trục hoành tại 3 điểm pb khi và chỉ khi (1) có 2 nghiệm pb khác -1
\(\Leftrightarrow\left\{{}\begin{matrix}f\left(-1\right)=1-2m+m+2\ne0\\\Delta'=m^2-m-2>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne3\\\left[{}\begin{matrix}m>2\\m< -1\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m< -1\\2< m< 3\\m>3\end{matrix}\right.\)
2,1
\(f'\left(x\right)=2sinx+2sin2x\)
\(f'\left(x\right)=0\Leftrightarrow2sinx+4sinx.cosx=0\)
\(\Leftrightarrow2sinx\left(1+2cosx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\cosx=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\dfrac{2\pi}{3}+k2\pi\\x=-\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
Do \(x\in\left[\dfrac{\pi}{2};\dfrac{3\pi}{2}\right]\Rightarrow x=\left\{\dfrac{2\pi}{3};\pi;\dfrac{4\pi}{3}\right\}\)
\(f''\left(x\right)=2cosx+4cos2x\)
\(f''\left(\dfrac{2\pi}{3}\right)=-3< 0\) ; \(f''\left(\pi\right)=2>0\) ; \(f''\left(\dfrac{4\pi}{3}\right)=-3< 0\)
\(\Rightarrow x=\left\{\dfrac{2\pi}{3};\dfrac{4\pi}{3}\right\}\) là 2 điểm cực đại của hàm số trên đoạn đã cho
\(x=\pi\) là điểm cực tiểu
2.2
\(\lim\limits_{x\rightarrow\pm\infty}\dfrac{x^2-5x+6}{x^2-4}=\lim\limits_{x\rightarrow\pm\infty}\dfrac{1-\dfrac{5}{x}+\dfrac{6}{x^2}}{1-\dfrac{4}{x^2}}=1\)
\(\Rightarrow y=1\) là tiệm cận ngang của ĐTHS
\(\lim\limits_{x\rightarrow2}\dfrac{x^2-5x+6}{x^2-4}=\lim\limits_{x\rightarrow2}\dfrac{\left(x-2\right)\left(x-3\right)}{\left(x-2\right)\left(x+2\right)}=\lim\limits_{x\rightarrow2}\dfrac{x-3}{x+2}=-\dfrac{1}{4}\) hữu hạn
\(\Rightarrow x=2\) không phải tiệm cận của ĐTHS
\(\lim\limits_{x\rightarrow-2}\dfrac{\left(x-2\right)\left(x-3\right)}{\left(x-2\right)\left(x+2\right)}=\lim\limits_{x\rightarrow-2}\dfrac{x-3}{x+2}=\infty\)
\(\Rightarrow x=-2\) là 1 TCĐ của ĐTHS
Vậy hàm số có TCĐ là \(x=-2\) và TCN \(y=1\)
2.3
Hàm số có 3 điểm cực trị khi:
\(1.\left(-2m\right)< 0\)
\(\Leftrightarrow m>0\)
(Hàm trùng phương có 3 cực trị khi a;c trái dấu hay \(ac< 0\))


