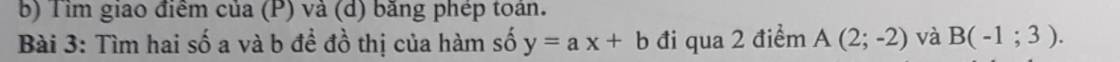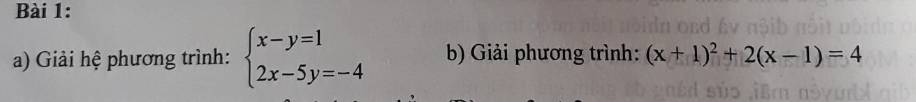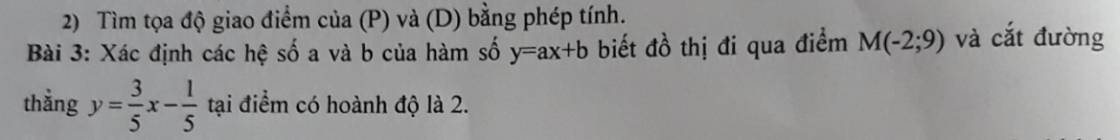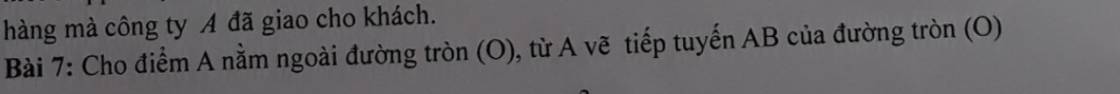
Bài 5: Công thức nghiệm thu gọn

a:

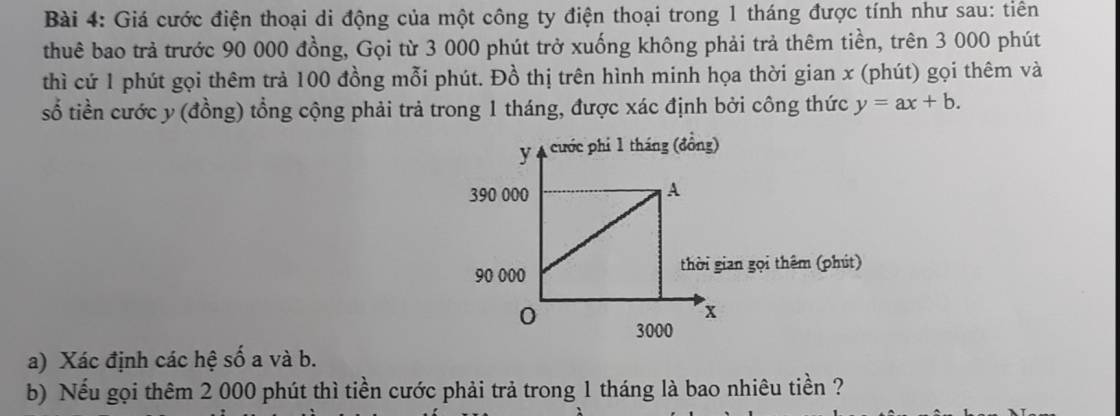
Đặt (d): y=ax+b

Theo đồ thị, ta thấy (d) đi qua B(0;90000) và A(3000;390000)

Thay x=0 và y=90000 vào (d), ta được:

a*0+b=90000

=>b=90000

=>(d): y=ax+90000

Thay x=3000 và y=390000 vào (d), ta được:

\(3000\cdot a+90000=390000\)

=>3000a=300000

=>a=100

Vậy: (d): y=100x+90000

b: Số tiền phải trả khi gọi thêm 2000 phút là:

100*2000+90000=200000+90000=290000(đồng)

Thay x=2 và y=-2 vào y=ax+b, ta được:

\(a\cdot2+b=-2\)

=>2a+b=-2(1)

Thay x=-1 và y=3 vào y=ax+b, ta được:

a*(-1)+b=3

=>-a+b=3(2)

Từ (1),(2) ta có hệ phương trình:

\(\left\{{}\begin{matrix}2a+b=-2\\-a+b=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3a=-5\\a-b=-3\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}a=-\dfrac{5}{3}\\b=a+3=-\dfrac{5}{3}+3=\dfrac{4}{3}\end{matrix}\right.\)

Bài 1:

a: \(\left\{{}\begin{matrix}2x-3y=14\\3x+y=10\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2x-3y=14\\9x+3y=30\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}11x=44\\3x+y=10\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=4\\y=10-3x=-2\end{matrix}\right.\)

b: \(x^2-8x=-15\)

=>\(x^2-8x+15=0\)

=>(x-3)(x-5)=0

=>\(\left[{}\begin{matrix}x-3=0\\x-5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=5\end{matrix}\right.\)

Bài 2:

a: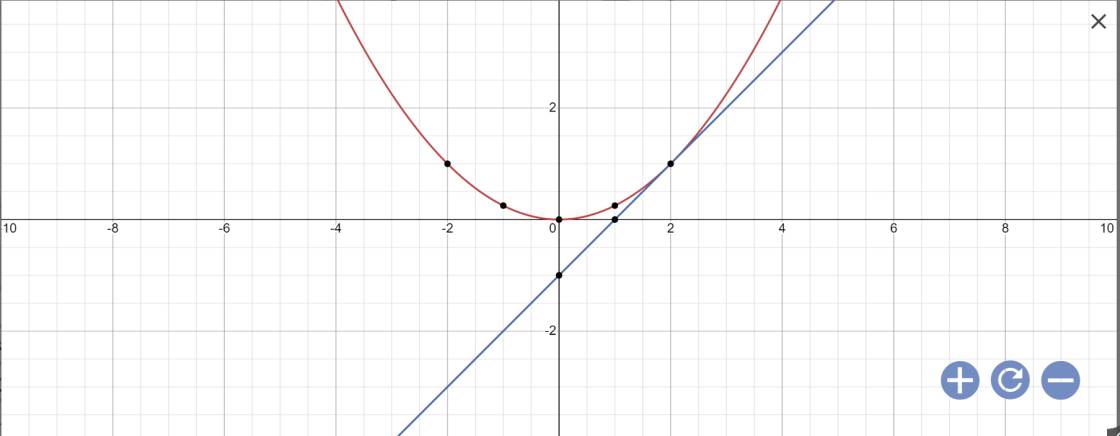 

b: Phương trình hoành độ giao điểm là:

\(\dfrac{1}{4}x^2=x-1\)

=>\(\dfrac{1}{4}x^2-x+1=0\)

=>\(\left(\dfrac{1}{2}x-1\right)^2=0\)

=>\(\dfrac{1}{2}x-1=0\)

=>x=2

Thay x=2 vào y=x-1, ta được:

y=2-1=1

Vậy: (P) cắt (d) tại A(2;1)

a: \(\left\{{}\begin{matrix}x-y=1\\2x-5y=-4\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2x-2y=2\\2x-5y=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-2y-2x+5y=2+4\\x-y=1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}3y=6\\x-y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\\x=y+1=3\end{matrix}\right.\)

b: \(\left(x+1\right)^2+2\cdot\left(x-1\right)=4\)

=>\(x^2+2x+1+2x-2-4=0\)

=>\(x^2+4x-5=0\)

=>(x+5)(x-1)=0

=>\(\left[{}\begin{matrix}x=-5\\x=1\end{matrix}\right.\)

a: Xét tứ giác MDEC có \(\widehat{MDC}=\widehat{MEC}=90^0\)

nên MDEC là tứ giác nội tiếp

b Xét ΔAEM vuông tại E và ΔADC vuông tại D có

\(\widehat{EAM}\) chung

Do đó: ΔAEM~ΔADC

=>\(\dfrac{AE}{AD}=\dfrac{AM}{AC}\)

=>\(AE\cdot AC=AM\cdot AD\)

c: Xét (O) có

ΔACK nội tiếp

AK là đường kính

Do đó: ΔACK vuông tại C

Xét (O) có

\(\widehat{ABC}\) là góc nội tiếp chắn cung AC

\(\widehat{AKC}\) là góc nội tiếp chắn cung AC

Do đó: \(\widehat{ABC}=\widehat{AKC}\)

Xét ΔABD vuông tại Dvà ΔAKC vuông tại C có

\(\widehat{ABD}=\widehat{AKC}\)

Do đó: ΔABD~ΔAKC

=>\(\dfrac{AB}{AK}=\dfrac{AD}{AC}\)

=>\(AB\cdot AC=AD\cdot AK=AK\cdot2R\)

a: Gọi giá ban đầu của 1 đôi giày là x(đồng)

(ĐK: x>0)

Giá của đôi giày thứ hai là \(x\cdot\left(1-30\%\right)=0,7x\left(đồng\right)\)

Giá của đôi giày thứ ba là \(x\cdot\left(1-50\%\right)=0,5x\left(đồng\right)\)

Tổng số tiền của 3 đôi giày là 1320000 nên ta có:

x+0,7x+0,5x=1320000

=>2,2x=1320000

=>x=600000(nhận)

Vậy: Giá ban đầu của 1 đôi giày là 600000 đồng

b: Số tiền phải trả khi mua 3 đôi giày là:

\(600000\cdot3\left(1-20\%\right)=1440000\left(đồng\right)\)
=>Nên chọn hình thức ở trong đề

Gọi số giáo viên đi tham quan là x(người)

(ĐK: \(x\in Z^+\))

Số học sinh đi tham quan là 250-x(người)

Số tiền phải trả tiền vé cho x giáo viên là:

\(x\cdot80000\cdot\left(1-5\%\right)=76000x\left(đồng\right)\)

Số tiền phải trả tiền vé cho 250-x học sinh là:

\(\left(250-x\right)\cdot60000\left(1-5\%\right)=57000\left(250-x\right)\left(đồng\right)\)

Tổng số tiền phải trả là 14535000 nên ta có:

76000x+57000(250-x)=14535000

=>76x+57(250-x)=14535

=>76x+14250-57x=14535

=>19x=285

=>x=15(nhận)

vậy: Số giáo viên đi tham quan là 15 người

Số học sinh đi tham quan là 250-15=235 người

a: Thay t=0 và h=2,56 vào h=at+b, ta được: 

\(a\cdot0+b=2,56\)

=>b=2,56

=>h=at+2,56

Thay t=2 và h=2,56+1,28=3,84 vào h=at+2,56, ta được:

2a+2,56=3,84

=>2a=1,28

=>a=0,64

=>h=0,64t+2,56

b: Để đạt chiều cao 6,7cm thì 0,64t+2,56=6,7

=>0,64t=6,7-2,56=4,14

=>\(t=\dfrac{4.14}{0,64}\simeq6\left(ngày\right)\)

Thay x=-2 và y=9 vào y=ax+b, ta được:

\(a\cdot\left(-2\right)+b=9\)

=>-2a+b=9(1)

Thay x=2 vào y=3/5x-1/5, ta được:

\(y=\dfrac{3}{5}\cdot2-\dfrac{1}{5}=1\)

Thay x=2 và y=1 vào y=ax+b, ta được:

\(2\cdot a+b=1\)(2)

Từ (1) và (2) ta có hệ phương trình:

\(\left\{{}\begin{matrix}-2a+b=9\\2a+b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2b=10\\2a+b=1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}b=5\\2a=1-5=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b=5\end{matrix}\right.\)

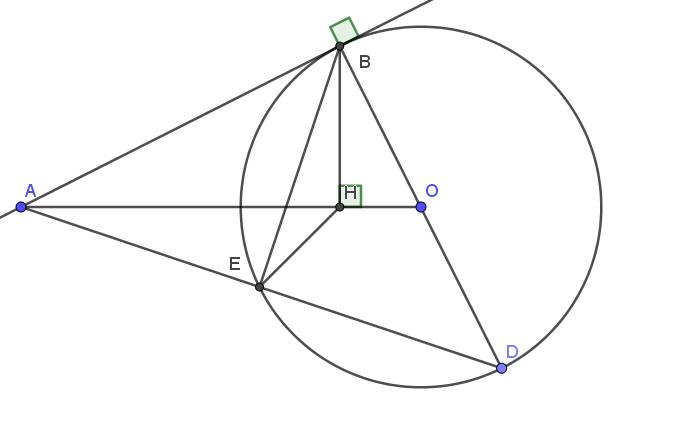
Lời giải:
a. 

Xét tam giác $ABE$ và $ADB$ có:

$\widehat{A}$ chung

$\widehat{ABE}=\widehat{ADB}$ (góc tạo bởi tiếp tuyến và dây cung thì bằng góc nt chắn cung đó, ở đây là cung EB)

$\Rightarrow \triangle ABE\sim \triangle ADB$ (g.g)

$\Rightarrow \frac{AB}{AD}=\frac{AE}{AB}$

$\Rightarrow AB^2=AE.AD$
b.

$\widehat{BED}=90^0$ (góc nt chắn nửa đường tròn)
$\Rightarrow \widehat{AEB}=180^0-\widehat{BED}=180^0-90^0=90^0$

Tứ giác $ABHE$ có $\widehat{AEB}=\widehat{AHB}=90^0$. Mà 2 góc này cùng nhìn cạnh $AB$ nên $ABHE$ là tgnt.

c.

Do $ABHE$ là tgnt nên $\widehat{AHE}=\widehat{ABE}$

Mà $\widehat{ABE}=\widehat{ADB}$ (đã cm ở phần a)

$\Rightarrow \widehat{AHE}=\widehat{ADB}$

Hình vẽ: