Lời giải:
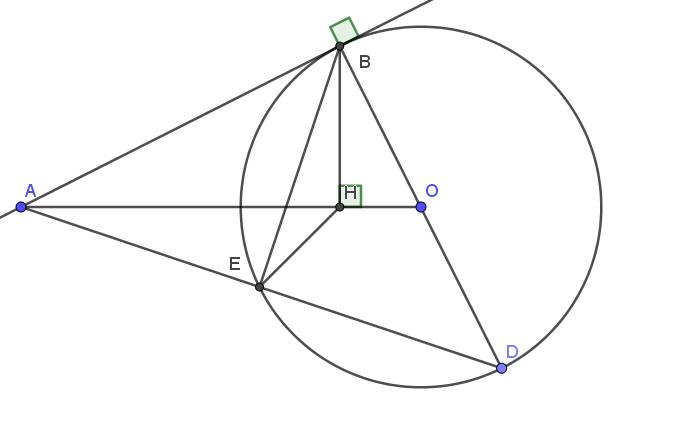
a.
Xét tam giác $ABE$ và $ADB$ có:
$\widehat{A}$ chung
$\widehat{ABE}=\widehat{ADB}$ (góc tạo bởi tiếp tuyến và dây cung thì bằng góc nt chắn cung đó, ở đây là cung EB)
$\Rightarrow \triangle ABE\sim \triangle ADB$ (g.g)
$\Rightarrow \frac{AB}{AD}=\frac{AE}{AB}$
$\Rightarrow AB^2=AE.AD$
b.
$\widehat{BED}=90^0$ (góc nt chắn nửa đường tròn)
$\Rightarrow \widehat{AEB}=180^0-\widehat{BED}=180^0-90^0=90^0$
Tứ giác $ABHE$ có $\widehat{AEB}=\widehat{AHB}=90^0$. Mà 2 góc này cùng nhìn cạnh $AB$ nên $ABHE$ là tgnt.
c.
Do $ABHE$ là tgnt nên $\widehat{AHE}=\widehat{ABE}$
Mà $\widehat{ABE}=\widehat{ADB}$ (đã cm ở phần a)
$\Rightarrow \widehat{AHE}=\widehat{ADB}$
Đúng 2
Bình luận (2)
