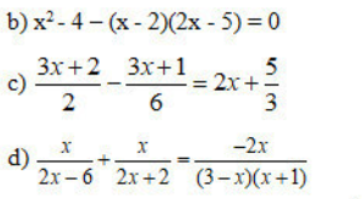Bài 3: Phương trình đưa được về dạng ax + b = 0

Cần câu nào?

Câu a chuyển vế 

Câu b nhóm nhân tử

Câu c chuyển vế=0 tạo mẫu chứng rồi lấy tử =0

câu còn lại lm tương tự

Câu cuối mỗi phân số +1 r làm

b: \(\Leftrightarrow\left(x-2\right)\left(x+2\right)-\left(x-2\right)\left(2x-5\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(x+2-2x+5\right)=0\)

=>(x-2)(7-x)=0

=>x=2 hoặc x=7

c: \(\Leftrightarrow3\left(3x+2\right)-3x-1=12x+20\)

=>9x+6-3x-1=12x+20

=>3x+5=12x+20

=>x=-5/3

d: \(\Leftrightarrow\dfrac{x\left(x+1\right)}{2\left(x-3\right)\left(x+1\right)}+\dfrac{x\left(x-3\right)}{2\left(x-3\right)\left(x+1\right)}=\dfrac{4x}{2\left(x-3\right)\left(x+1\right)}\)

Suy ra: \(x^2+x+x^2-3x-4x=0\)

\(\Leftrightarrow2x\left(x-3\right)=0\)

=>x=0(nhận) hoặc x=3(loại)

Em có thể gõ rõ để ra hơn được không em?

a: =>6-2x-2x-5=4x+3

=>-4x+1-4x-3=0

=>-8x-2=0

=>8x=-2

hay x=-1/4

b: =>3(3-2x)+4(-x+3)=12

=>9-6x-4x-12=12

=>-10x-3=12

=>-10x=15

hay x=-3/2

Gọi vận tốc xe máy đi từ TP HCM đến Cần Thơ là v₁= 40 km/h

      vận tốc ô tô đi từ TP HCM đến Cần Thơ là v₂= 60 (km/h)

Gọi G là vị trí hai xe gặp nhau

Thời gian hai xe đi đến lúc gặp nhau: \(\dfrac{AG}{v_1}=\dfrac{AG}{v_2}+2=y\)

Phương trình biểu thị việc ô tô gặp xe máy sau y giờ kể từ lúc ô tô khởi hành là:\(y=\dfrac{x}{60}+2\) (giờ)

A 3x-4x=-9-3

    -x=-12

     x=12

B 3.2x -5x +1=5+0.2x

  3.2x-5x-0.2x=5-1

  -2x=4

 x=-2

C 1.5-x-2=-3x-0.3

  -x+3x=-0.3-1.5+2

  2x =0.2

  x=0.1

E 2/3-1/2x-1=-x+1

  -1/2x+x=1+1-2/3

  1/2x=4/3

  x=8/3

F 3t-4+13+2t+4-3t

  =3t+2t-3t-4+13+4

  =2t+13

Bài 2:

a. Thay a = 3 vào (1), ta được:

\(2.3.x-3.\left(3+1\right)x=3-2\)

\(\Leftrightarrow6x-12x=1\)

\(\Leftrightarrow-6x=1\)

\(\Leftrightarrow x=-\dfrac{1}{6}\)

b. Thay \(x=-2\) vào (1), ta được:

\(2a.\left(-2\right)-3\left(a+1\right)\left(-2\right)=a-2\)

\(\Leftrightarrow-4a+6\left(a+1\right)=a-2\)

\(\Leftrightarrow-4a+6a+6=a-2\)

\(\Leftrightarrow a=-8\)

Vậy khi \(a=-8\) thì (1) có nghiệm \(x=-2\)

\(1a.\left(7x-8\right)+2\left(3x-4\right)=12\)

\(\Leftrightarrow7x-8+6x-8=12\)

\(\Leftrightarrow13x=28\)

\(\Leftrightarrow x=\dfrac{28}{13}\)

\(1b.3x+8-5\left(x-7\right)=x+13\)

\(\Leftrightarrow3x+8-5x+7=x+13\)

\(\Leftrightarrow-3x=-2\)

\(\Leftrightarrow x=\dfrac{2}{3}\)

a.- Xét △KDC có:

DC//BF (ABCD là hình bình hành).

=>\(\dfrac{CK}{KF}=\dfrac{DK}{BK}\) (định lí Ta-let). (1)

- Xét △KDM có:

MD//BD (ABCD là hình bình hành).

=>\(\dfrac{DK}{BK}=\dfrac{MK}{CK}\) (định lí Ta-let). (2)

- Từ (1) và (2) suy ra:

\(\dfrac{CK}{KF}=\dfrac{KM}{CK}\). Vậy \(CK^2=KM.KF\)

b. - Xét △KDC có:

DC//BF (ABCD là hình bình hành).

=> \(\dfrac{DK}{BK}=\dfrac{CK}{CF}\) (định lí Ta-let). (3)

- Xét △KDM có:

MD//BD (ABCD là hình bình hành).

=>\(\dfrac{DK}{BK}=\dfrac{MK}{CM}\) (định lí Ta-let). (4)

- Từ (3) và (4) suy ra:  \(\dfrac{CK}{CF}=\dfrac{MK}{CM}\)

=>\(\dfrac{CK}{CF}=\dfrac{MK}{CM}=\dfrac{CK+MK}{CF+CM}\) (t/c tỉ lệ thức).

=>\(\dfrac{CK}{CF}=\dfrac{CM}{CF+CM}\)

=>\(CK=\dfrac{CM.CF}{CF+CM}\)
=>\(\dfrac{1}{CK}=\dfrac{CF+CM}{CM.CF}\)

=>\(\dfrac{1}{CK}=\dfrac{1}{CF}+\dfrac{1}{CM}\)

c.

Do \(\widehat{DBC}=\widehat{CBE}\Rightarrow BC\) là phân giác trong góc \(\widehat{DBE}\) trong tam giác BDE

Theo định lý phân giác: \(\dfrac{BE}{BD}=\dfrac{CE}{CD}\) (1)

Trong tam giác MCD, do \(AF||CD\) nên theo định lý Talet:  \(\dfrac{AF}{CD}=\dfrac{MF}{MC}\)

Trong tam giác MCE, do \(BF||CE\) nên theo định lý Talet: \(\dfrac{BF}{CE}=\dfrac{MF}{MC}\)

\(\Rightarrow\dfrac{AF}{CD}=\dfrac{BF}{CE}\Rightarrow\dfrac{CE}{CD}=\dfrac{BF}{AF}\) (2)

(1);(2) \(\Rightarrow\dfrac{BF}{AF}=\dfrac{BE}{BD}\) (đpcm)

d.

Do \(BI\perp BC\), mà BC là đường phân giác trong nên BC là phân giác ngoài góc \(\widehat{DBE}\) của tam giác BDE

Theo định lý phân giác: \(\dfrac{IE}{ID}=\dfrac{BE}{BD}\)

Theo câu c ta có \(\dfrac{BE}{BD}=\dfrac{CE}{CD}\)

\(\Rightarrow\dfrac{IE}{ID}=\dfrac{CE}{CD}\Rightarrow IE.CD=ID.CE\)

a, <=> x = -4 

b, <=> 6x + 2 = -2x + 5 <=> 8x = 3 <=> x = 3/8 

c, <=> 5x + 2x - 2 = 4x + 7 <=> 2x = 9 <=> x = 9 /2 

d, <=> 10x^2 - 10x^2 - 15x = 15 <=> x = -1 

a, <=> x = -4 

b, <=> 6x + 2 = -2x + 5 <=> 8x = 3 <=> x = 3/8 

c, <=> 5x + 2x - 2 = 4x + 7 <=> 2x = 9 <=> x = 9 /2 

d <=> 10x^2 - 10x^2 - 15x = 15 <=> x = -1 

a) x=-4

b)4x=3

x=3/4

c)3x=9

x=3

d) 15x=15

x=1

4, \(\Leftrightarrow4x+4+9\left(2x+1\right)=4x+6\left(x+1\right)+7+12x\)

\(\Leftrightarrow22x+13=22x+13\)vậy pt có vô số nghiệm 

5, \(\dfrac{2x}{3}+\dfrac{2x-1}{6}=4-\dfrac{x}{3}\Rightarrow4x+2x-1=24-2x\)

\(\Leftrightarrow8x=25\Leftrightarrow x=\dfrac{25}{8}\)

6, \(\dfrac{x-1}{2}+\dfrac{x-1}{4}=1-\dfrac{2\left(x-1\right)}{3}\Rightarrow6x-6+3x-3=12-8\left(x-1\right)\)

\(\Leftrightarrow9x-9=20-8x\Leftrightarrow17x=29\Leftrightarrow x=\dfrac{29}{17}\)