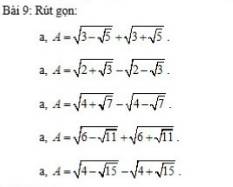\(B=\dfrac{x^3-3x+\left(x^2-1\right)\sqrt{x^2-4}-2}{x^3-3x+\left(x^2-1\right)\sqrt{x^2-4}+2}\)với x > 0 rút gọn biểu thức ( cho em xin lời giải chi tiết ạ )
Bài 3: Liên hệ giữa phép nhân và phép khai phương
\(\sqrt{x+2\sqrt{2x-4}}+\sqrt{x-2\sqrt{2x-4}}=2\sqrt{2}\)giải phương trình ( cho em xin lời giải chi tiết ạ )
\(\sqrt{x+2\sqrt{2x-4}}+\sqrt{x-2\sqrt{2x-4}}=2\sqrt{2}\)
\(\Leftrightarrow\sqrt{x+2\sqrt{2\left(x-2\right)}}+\sqrt{x-2\sqrt{2\left(x-2\right)}}=2\sqrt{2}\)
\(\Leftrightarrow2x+2\sqrt{\left[x+2\sqrt{2\left(x-2\right)}\text{ }\right]\left[x-2\sqrt{2\left(x-2\right)}\text{ }\right]}=8\)
\(\Leftrightarrow2\sqrt{\left[x+2\sqrt{2\left(x-2\right)}\text{ }\right]\left[x-2\sqrt{2\left(x-2\right)}\text{ }\right]}=8-2x\)
\(\Leftrightarrow4\left[x+2\sqrt{2\left(x-2\right)}\text{ }\right]\left[x-2\sqrt{2\left(x-2\right)}\text{ }\right]=64-32x+4x^2\)
\(\Leftrightarrow4x^2-32x+64=64-32x+4x^2+\)
\(\Leftrightarrow64=64\) (Đúng)
⇒ Phương trình có vô số nghiệm.
Vậy \(S=\mathbb R\).
Đúng 1
Bình luận (6)
\(\sqrt{x+2\sqrt{2x-4}}+\sqrt{x-2\sqrt{2x-4}}=2\sqrt{2}\)
ĐK: \(x\ge2\), PT tương đương với:
\(x+2\sqrt{2x-4}+2\sqrt{\left(x+2\sqrt{2x-4}\right)\left(x-2\sqrt{2x-4}\right)}+x-2\sqrt{2x-4}=8\)
\(\Leftrightarrow2x+2\sqrt{x^2-4\left(2x-4\right)}=8\)
\(\Leftrightarrow2x+2\sqrt{x^2-8x+16}=8\\ \Leftrightarrow x+\left|x-4\right|=8\)
Với x < 4 => \(x+4-x=8\)
\(\Leftrightarrow4=8\) (loại)
Với \(x\ge4\) => \(x+x-4=8\)
\(\Leftrightarrow x=6\) (thỏa mãn)
Đúng 1
Bình luận (6)
\(\sqrt{\dfrac{27\left(x-1\right)^2}{12}}+\dfrac{3}{2}-\left(x-2\right)\sqrt{\dfrac{50x^2}{8\left(x-2\right)^2}}\)rút gọn biểu thức : Đk : 1 <x<2 ( cho em xin lời giải chi tiết ạ )
`\sqrt{[27(x-1)^2]/12} +3/2 - (x - 2)\sqrt{[50x^2]/[8(x-2)^2]}` `(1 < x < 2)`
`=\sqrt{[3(x-1)]^2 .3}/\sqrt{2^2 .3} + 3/2 - (x - 2) \sqrt{(5x)^2 . 2}/\sqrt{[2(x - 2)]^2 . 2}`
`=[3\sqrt{3}|x-1|]/[2\sqrt{3}]+3/2-(x-2)[5\sqrt{2}|x|]/[2\sqrt{2}|x-2|]`
`=[3(x-1)]/2+3/2-[5x(x-2)]/[2(2-x)]` (Vì `1 < x < 2`)
`=3/2x - 3/2 + 3/2 + 5/2x`
`=4x`
Đúng 1
Bình luận (1)
a: =1/căn 2(căn 6-2căn 5+căn 6+2căn 5)
=1/căn2(căn 5-1+căn 5-1)
=2*căn 5/2
=căn 10
b: =1/căn 2(căn 4+2căn 3-căn 4-2căn 3)
=1/căn 2(căn 3+1-căn 3+1)
=1/căn 2*2=căn 2
c: =1/căn 2(căn 8+2 căn 7-căn 8-2căn 7)
=1/căn 2(căn 7+1-căn 7+1)
=1/căn2 *2=căn 2
d: =1/căn 2(căn 12-2căn 11+căn 12-2căn 11)
=1/căn 2(căn 11-1+căn 11-1)
=2*căn 11/2=căn 22
e: =1/căn 2(căn 8-2căn 15-căn 8+2căn 15)
=1/căn 2(căn 5-căn 3-căn 5-căn 3)
=-2*căn 3/2=-căn6
Đúng 0
Bình luận (0)
giải hộ mk bài này:
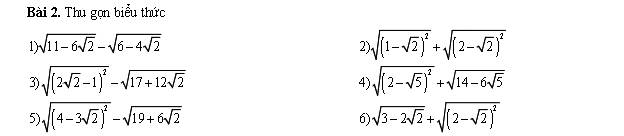
1) \(\sqrt{11-6\sqrt{2}}-\sqrt{6-4\sqrt{2}}\)
\(=\sqrt{9-6\sqrt{2}+2}-\sqrt{4-4\sqrt{2}+2}\)
\(=\sqrt{3^2-2\cdot3\cdot\sqrt{2}+\left(\sqrt{2}\right)^2}-\sqrt{2^2-2\cdot2\cdot\sqrt{2}\cdot\left(\sqrt{2}\right)^2}\)
\(=\sqrt{\left(3-\sqrt{2}\right)^2}-\sqrt{\left(2-\sqrt{2}\right)^2}\)
\(=\left|3-\sqrt{2}\right|-\left|2-\sqrt{2}\right|\)
\(=3-\sqrt{2}-2+\sqrt{2}=1\)
2) \(\sqrt{\left(1-\sqrt{2}\right)^2}-\sqrt{\left(2-\sqrt{2}\right)^2}\)
\(=\left|1-\sqrt{2}\right|-\left|2-\sqrt{2}\right|\)
\(=\sqrt{2}-1+2-\sqrt{2}\)
\(=1\)
3) \(\sqrt{\left(2\sqrt{2}-1\right)^2}-\sqrt{17+12\sqrt{2}}\)
\(=\sqrt{\left(2\sqrt{2}-1\right)^2}-\sqrt{9+12\sqrt{2}+8}\)
\(=\sqrt{\left(2\sqrt{2}-1\right)^2}-\sqrt{3^2+2\cdot3\cdot2\sqrt{2}+\left(2\sqrt{2}\right)^2}\)
\(=\sqrt{\left(2\sqrt{2}-1\right)^2}-\sqrt{\left(3+2\sqrt{2}\right)^2}\)
\(=\left|2\sqrt{2}-1\right|-\left|3+2\sqrt{2}\right|\)
\(=2\sqrt{2}-1-3-2\sqrt{2}=-4\)
4) \(\sqrt{\left(2-\sqrt{5}\right)^2}+\sqrt{14-6\sqrt{5}}\)
\(=\sqrt{\left(2-\sqrt{5}\right)^2}+\sqrt{9-6\sqrt{5}+5}\)
\(=\sqrt{\left(2-\sqrt{5}\right)^2}+\sqrt{3^2-2\cdot3\cdot\sqrt{5}+\left(\sqrt{5}\right)^2}\)
\(=\sqrt{\left(2-\sqrt{5}\right)^2}+\sqrt{\left(3-\sqrt{5}\right)^2}\)
\(=\left|2-\sqrt{5}\right|+\left|3-\sqrt{5}\right|\)
\(=\sqrt{5}-2+3-\sqrt{5}=1\)
5) \(\sqrt{\left(4-3\sqrt{2}\right)^2}-\sqrt{19+6\sqrt{2}}\)
\(=\sqrt{\left(4-3\sqrt{2}\right)^2}-\sqrt{18+6\sqrt{2}+1}\)
\(=\sqrt{\left(4-3\sqrt{2}\right)^2}-\sqrt{\left(3\sqrt{2}\right)^2+2\cdot3\sqrt{2}\cdot1+1^2}\)
\(=\sqrt{\left(4-3\sqrt{2}\right)^2}-\sqrt{\left(3\sqrt{2}+1\right)^2}\)
\(=\left|4-3\sqrt{2}\right|-\left|3\sqrt{2}+1\right|\)
\(=3\sqrt{2}-4-3\sqrt{2}-1=-5\)
6) \(\sqrt{3-2\sqrt{2}}+\sqrt{\left(2-\sqrt{2}\right)^2}\)
\(=\sqrt{2-2\sqrt{2}+1}+\sqrt{\left(2-\sqrt{2}\right)^2}\)
\(=\sqrt{\left(\sqrt{2}\right)^2-2\cdot\sqrt{2}\cdot1+1^2}+\sqrt{\left(2-\sqrt{2}\right)^2}\)
\(=\sqrt{\left(\sqrt{2}-1\right)^2}+\sqrt{\left(2-\sqrt{2}\right)^2}\)
\(=\sqrt{2}-1+2-\sqrt{2}=1\)
Đúng 2
Bình luận (0)
1: =3-căn 2-2+căn 2=1
2: \(=\sqrt{2}-1+2-\sqrt{2}=1\)
3: \(=2\sqrt{2}-1-3-2\sqrt{2}=-4\)
4: \(=\sqrt{5}-2+3-\sqrt{5}=1\)
5: \(=3\sqrt{2}-4-3\sqrt{2}-1=-5\)
6: \(=\sqrt{2}-1+2-\sqrt{2}=1\)
Đúng 0
Bình luận (0)
Giải PT:
a) √ x-5=3
b) √ x-10=-2
c) √ 2x-1=√ 5
d) √ 4-5x=12
e)√ 49(1-2x+x^2)-35=0
f) √ x^2-9-5√ x+3=0a: =>x-5=9
=>x=14
b: căn x-10=-2
=>\(x\in\varnothing\)
c: căn 2x-1=căn 5
=>2x-1=5
=>2x=6
=>x=3
d: căn 4-5x=12
=>4-5x=144
=>5x=-140
=>x=-28
e: =>7|x-1|=35
=>|x-1|=5
=>x-1=5 hoặc x-1=-5
=>x=6 hoặc x=-4
f: =>\(\sqrt{x+3}\left(\sqrt{x-3}-5\right)=0\)
=>x+3=0 hoặc x-3=25
=>x=28 hoặc x=-3
Đúng 1
Bình luận (0)
Phân tích thành nhân tử:
a) a - 5√a
b) a - 7 với a > 0
c) a + 4√a + 4
d) √xy - 4√x + 3√y - 12
a) \(a-5\sqrt{a}\)
\(=\sqrt{a}\left(\sqrt{a}-\sqrt{5}\right)\)
b) \(a-7\)
\(=\left(\sqrt{a}-\sqrt{7}\right)\left(\sqrt{a}+\sqrt{7}\right)\)
c) \(a+4\sqrt{a}+4\)
\(=\left(\sqrt{a}+2\right)^2\)
d) \(\sqrt{xy}-4\sqrt{x}+3\sqrt{y}-12\)
\(=\sqrt{x}\left(\sqrt{y}-4\right)+3\left(\sqrt{y}-4\right)\)
\(=\left(\sqrt{x}+3\right)\left(\sqrt{y}-4\right)\)
Đúng 2
Bình luận (0)
a: \(a-5\sqrt{a}=\sqrt{a}\left(\sqrt{a}-5\right)\)
b: \(a-7=\left(\sqrt{a}-\sqrt{7}\right)\left(\sqrt{a}+\sqrt{7}\right)\)
c: \(a+4\sqrt{a}+4=\left(\sqrt{a}+2\right)^2\)
d: \(\sqrt{xy}-4\sqrt{x}+3\sqrt{y}-12\)
=căn x(căn y-4)+3(căn y-4)
=(căn y-4)(căn x+3)
Đúng 2
Bình luận (0)
\(a,a-5\sqrt{a}=\sqrt{a}\left(\sqrt{a}-5\right)\\ b,a-7=\left(\sqrt{a}\right)^2-\left(\sqrt{7}\right)^2=\left(\sqrt{a}-\sqrt{7}\right)\left(\sqrt{a}+\sqrt{7}\right)\\ c,a+4\sqrt{a}+4=\left(\sqrt{a}\right)^2+2\sqrt{a}.2+2^2=\left(\sqrt{a}+2\right)^2\\ d,Sửa.đề:\sqrt{x}.\sqrt{y}-4\sqrt{x}+3\sqrt{y}-12\\ =\sqrt{x}\left(\sqrt{y}-4\right)+3.\left(\sqrt{y}-4\right)=\left(\sqrt{x}+3\right)\left(\sqrt{y}-4\right)\)
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
Không dùng máy tính hoặc bảng số, chứng minh rằng:
√3 + 2 < √2 (√3 + 1)
\(\sqrt{2}\left(\sqrt{3}+1\right)\)
\(=\sqrt{6}+\sqrt{2}\)
Ta có: \(\left(\sqrt{6}+\sqrt{2}\right)^2=8+4\sqrt{3}\)
Và: \(\left(\sqrt{3}+2\right)^2=7+4\sqrt{3}\)
Ta thấy: \(8+4\sqrt{3}>7+4\sqrt{3}\)
Hay: \(\sqrt{2}\left(\sqrt{3}+1\right)>\sqrt{3}+2\) (đpcm)
Đúng 2
Bình luận (0)
Rút gọn các biểu thức sau:
a) √ 3 +√ 8-2√ 15
b) √ x-1-2√x-2
a: =căn 3+căn 5-căn 3=căn5
b: \(=\sqrt{x-2-2\sqrt{x-2}+1}=\sqrt{\left(\sqrt{x-2}-1\right)^2}\)
\(=\left|\sqrt{x-2}-1\right|\)
Đúng 2
Bình luận (1)
\(\sqrt{3,2\:.\:7,2\:.\:49\:}\)
\(\sqrt{2,5\: .\: 12,5\: .20\: }\)
\(\sqrt{1,5}\) . \(\sqrt{\dfrac{2}{3}}\)
\(\sqrt{50\:.\:98\:}\)
Giúp mình vss mình đang cần gấp , cảm ơn nhìuuu ạaa🌷
a: =căn 16/5*36/5*49=7*4*9/5=252/5
b: =căn 250*2,5=căn 625=25
c: =căn 3/2*2/3=1
d: =5*căn 2*7*căn 2=70
Đúng 1
Bình luận (0)