Bài 1: Sự xác định đường tròn. Tính chất đối xứng của đường tròn

1. Nhắc lại về đường tròn

Ở lớp 6, ta đã biết:

Đường tròn tâm \(O\), bán kính \(R\left(R>0\right)\) là hình gồm các điểm cách điểm \(O\) một khoảng bằng \(R\).

- Đường tròn tâm \(O\) bán kính \(R\) được kí hiệu là \(\left(O;R\right)\). Trong trường hợp không quan tâm đến bán kính, ta có thể kí hiệu là \(\left(O\right)\).

- Khi điểm \(M\) thuộc đường tròn tâm \(O\), ta nói điểm \(M\) nằm trên đường tròn \(\left(O\right)\) hay đường tròn \(\left(O\right)\) đi qua điểm \(M\).

Ghi nhớ:

• Điểm \(M\) thuộc đường tròn \(\left(O;R\right)\) khi và chỉ khi \(OM=R\).
• Điểm \(M\) nằm trong đường tròn \(\left(O;R\right)\) khi và chỉ khi \(OM< R\).
• Điểm \(M\) nằm ngoài đường tròn \(\left(O;R\right)\) khi và chỉ khi \(OM>R\).

Ví dụ: Cho tam giác \(OHK\) như hình vẽ. So sánh các góc \(\widehat{OHK};\widehat{OKH}\)?

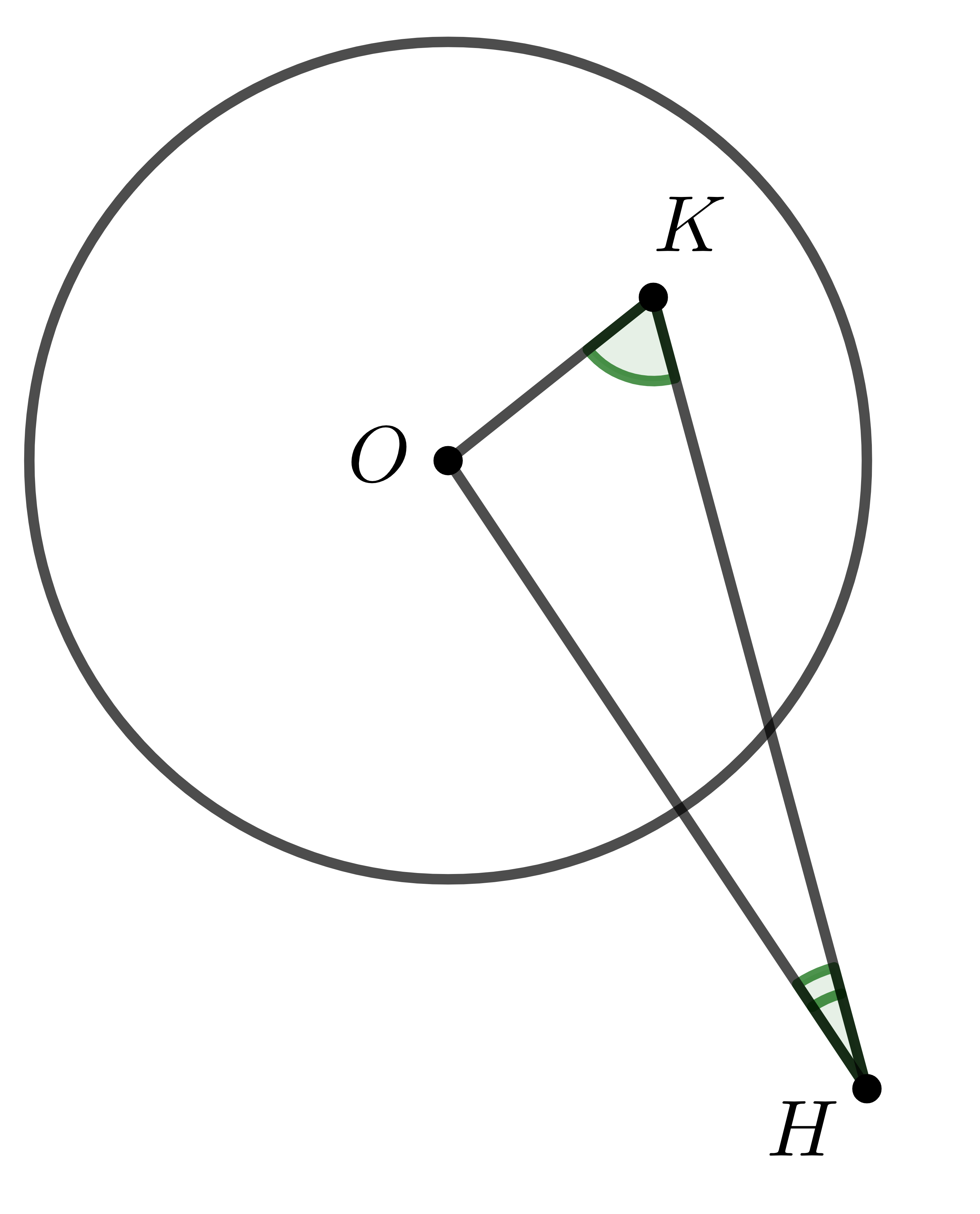
Ta có: \(K\) nằm trong đường tròn \(\left(O;R\right)\) nên \(OK< R\). \(H\) nằm ngoài đường tròn \(\left(O;R\right)\) nên \(OH>R\).

\(\Rightarrow OH>OK\) \(\Rightarrow\widehat{OKH}>\widehat{OHK}\) (tính chất: cạnh đối diện với góc lớn hơn thì lớn hơn).

2. Cách xác định một đường tròn

Ta đã biết:

• Một đường tròn hoàn toàn xác định khi biết tâm và bán kính của nó.
• Khi biết một đoạn thẳng là đường kính của một đường tròn thì trung điểm đoạn thẳng là tâm của đường tròn, bán kính của nó là nửa độ dài đoạn thẳng.

Định lí: Ta vẽ được một và chỉ một đường tròn đi qua 3 điểm không thẳng hàng.

Chú ý: Không vẽ được đường tròn nào đi qua 3 điểm thẳng hàng.

Thật vậy: Giả sử đường tròn \(\left(O\right)\) đi qua 3 điểm thẳng hàng \(A,B,C\)

\(\Rightarrow O\) là giao điểm của trung trực \(d_1\) của đoạn \(AB\) và trung trực \(d_2\) của đoạn \(BC\).

Do \(d_1,d_2\) song song nhau nên không tồn tại điểm \(O\) như thế.

Ta đã biết:

Một đường tròn đi qua cả 3 đỉnh của tam giác \(ABC\) được gọi là đường tròn ngoại tiếp tam giác \(ABC\), còn tam giác \(ABC\) được gọi là tam giác nội tiếp đường tròn.

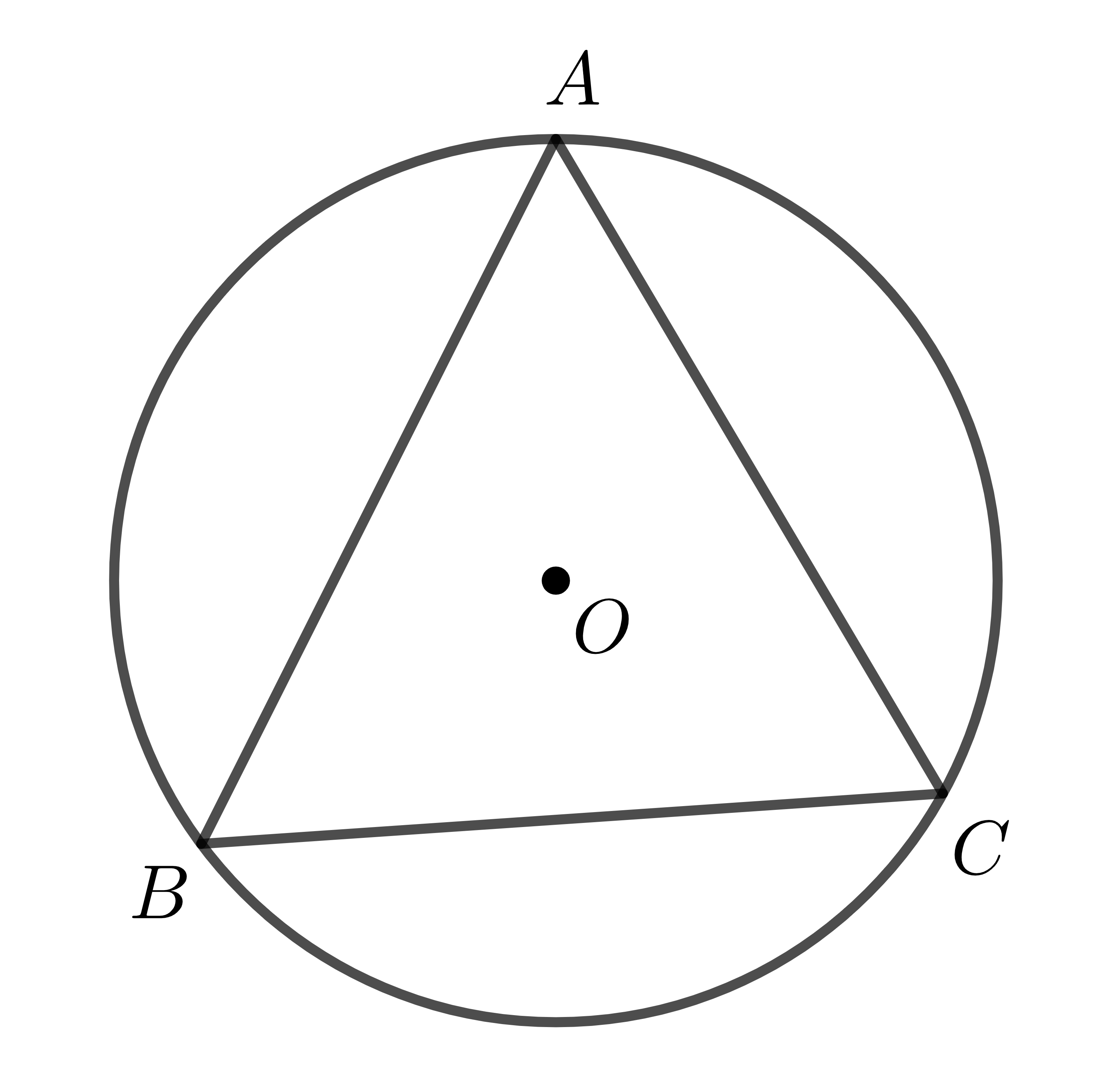
 Ta dễ thấy: Để \(O\) là tâm đường tròn ngoại tiếp tam giác \(ABC\) thì \(OA=OB=OC\)

\(\Rightarrow O\) phải nằm trên các đường trung trực của các đoạn thẳng \(AB,BC,AC\).

Như vậy ta có kết luận:

Tâm đường tròn ngoại tiếp tam giác là giao điểm 3 đường trung trực của tam giác đó.

3. Tâm đối xứng 

Đường tròn là hình có tâm đối xứng. Tâm đối xứng của đường tròn chính là tâm của đường tròn đó.

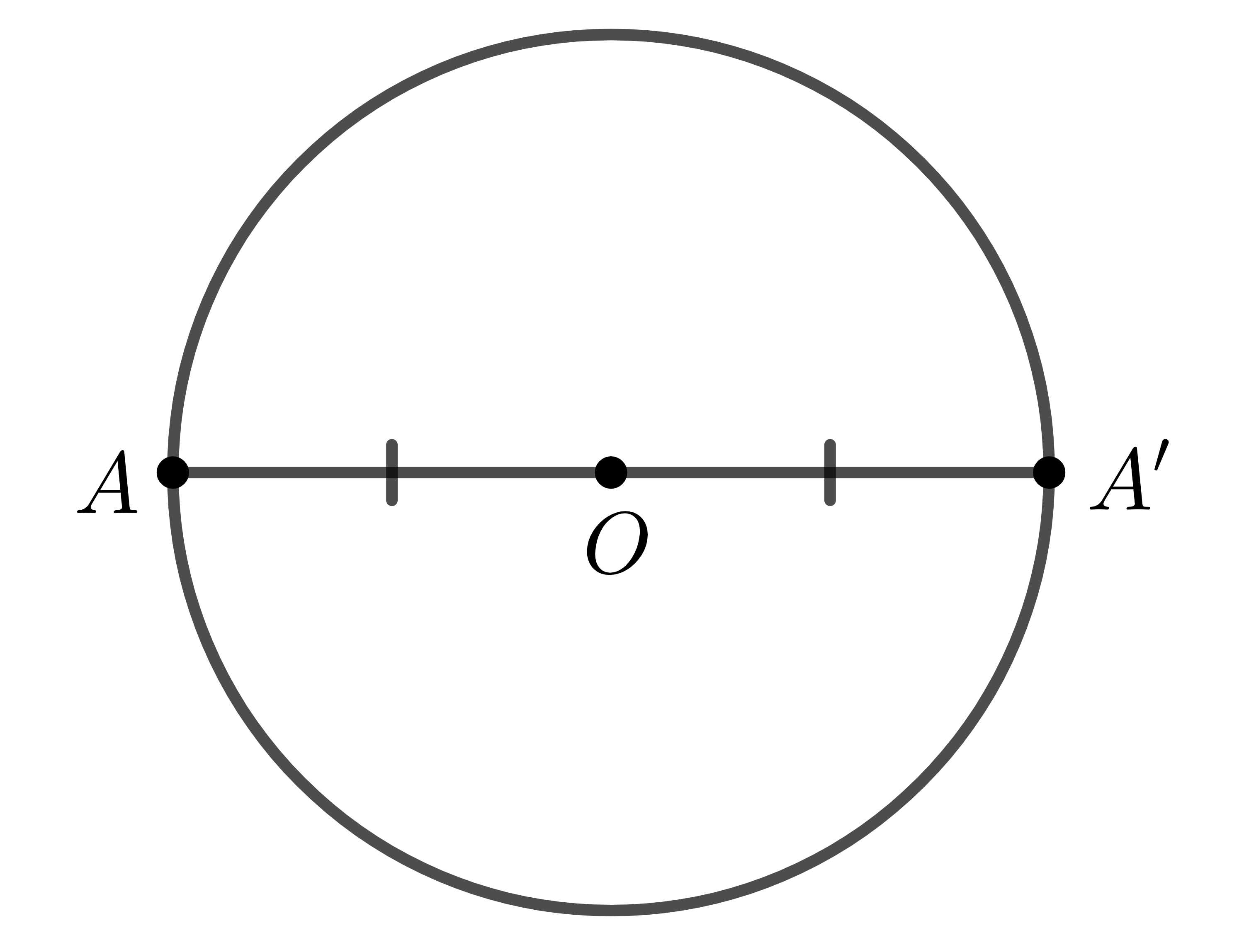
4. Trục đối xứng

Đường tròn là hình có trục đối xứng. Bất kì đường tròn nào cũng là trục đối xứng của đường tròn.