Bài 6: Mặt phẳng tọa độ

1. Một số ví dụ thực tế về tọa độ

Ví dụ 1: Ở các lớp dưới ta đã biết: Mỗi địa điểm trên bản đồ địa lí đều được xác định bởi một cặp gồm hai số (tọa độ địa lí) là kinh độ và vĩ độ. Chẳng hạn: Tọa độ địa lí của mũi Cà Mau là: 

\(\left\{{}\begin{matrix}104^040'Đ\\8^030'B\end{matrix}\right.\)

Ví dụ 2: Quan sát bàn cờ vua:

Trên bàn cờ vua, người ta kí hiệu cho từng hàng, từng cột bằng các chữ cái và các số riêng. Chẳng hạn: 2 quân xe đen đang ở cột \(a\) - hàng \(8\) và cột \(h\) - hàng \(8\), ta nói vị trí (tọa độ) của chúng trên bàn cờ là ô \(a8\) và ô \(h8\). Bằng cách đó, ta có thể gọi tên của mọi vị trí trên bàn cờ.

Trong toán học, ta xác định vị trí của một điểm trên mặt phẳng người ta thường dùng một cặp số. Sau đây, ta đi tìm hiểu cách xác định cặp số đó.

2. Mặt phẳng tọa độ

Trên mặt phẳng, ta vẽ hai trục \(Ox,Oy\) vuông góc với nhau và cắt nhau tại gốc của mỗi trục. Ta được hệ trục tọa độ \(Oxy\).

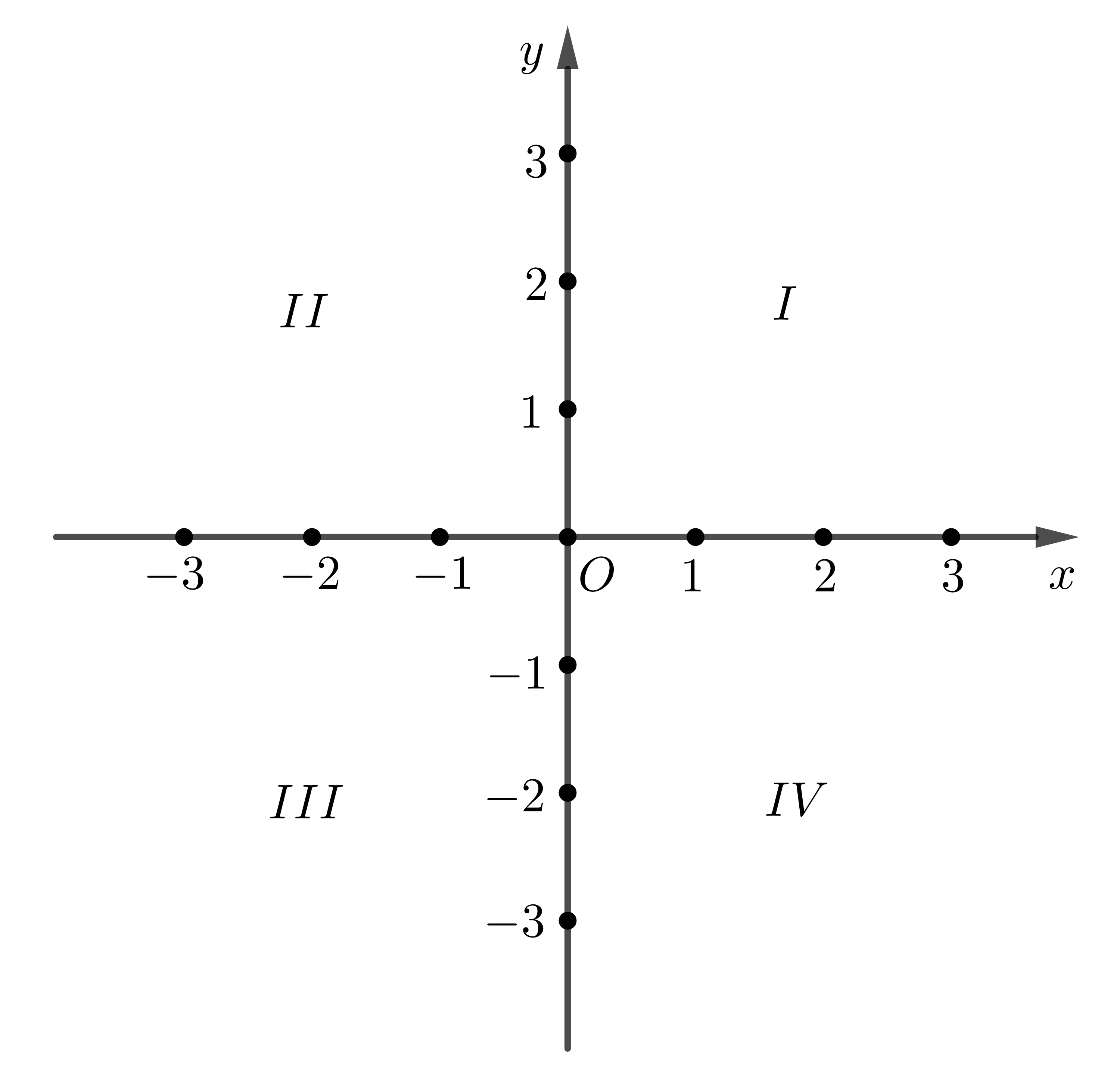
• Các trục \(Ox,Oy\) gọi là các trục tọa độ. \(Ox\) gọi là trục hoành, \(Oy\) gọi là trục tung. Người ta thường vẽ \(Ox\) nằm ngang, còn \(Oy\) thẳng đứng.
• Giao điểm \(O\) biểu diễn số \(0\) của cả hai trục gọi là gốc tọa độ.
• Mặt phẳng có hệ trục tọa độ \(Oxy\) gọi là mặt phẳng tọa độ \(Oxy\).
• Hai trục tọa độ chia mặt phẳng thành 4 góc: Góc phần tư thứ \(I,II,III,IV\) theo thứ tự ngược chiều quay của hai kim đồng hồ.

Chú ý: Các đơn vị dài trên hai trục tọa độ được chọn bằng nhau (nếu không nói gì thêm).

3. Tọa độ của một điểm trong mặt phẳng tọa độ

Trong mặt phẳng tọa độ \(Oxy\), xét điểm \(P\) bất kì. Từ \(P\) kẻ các đường vuông góc với các trục tọa độ. Trong hình trên, các đường này cắt trục hoành tại điểm \(2\) và cắt trục tung tại điểm \(3\). Khi đó, ta gọi cặp số \(\left(2;3\right)\) là tọa độ của điểm \(P\) và kí hiệu \(P\left(2;3\right).\)

• Số \(2\) gọi là hoành độ của \(P\).
• Số \(3\) gọi là tung độ của \(P\).

Ví dụ: Trong hình trên, điểm \(Q\) có tọa độ là \(\left(-2;-2\right)\). 

Chú ý: Hoành độ luôn là số đứng trước.

Tổng quát: Trong mặt phẳng tọa độ \(Oxy\):

• Mỗi điểm \(M\) xác định một cặp số \(\left(x_0;y_0\right)\).Ngược lại, mỗi cặp số \(\left(x_0;y_0\right)\) xác định một điểm \(M\).
• Cặp số \(\left(x_0;y_0\right)\) gọi là tọa độ của điểm \(M\). \(x_0\) là hoành độ và \(y_0\) là tung độ của điểm \(M\).
• Điểm \(M\) có tọa độ \(\left(x_0;y_0\right)\) được kí hiệu \(M\left(x_0;y_0\right)\).

Nhận xét:

1. Để tìm tọa độ của một điểm trên mặt phẳng, ta kẻ vuông góc từ điểm đó vào từng trục tọa độ. Nếu các đường vuông góc cắt \(Ox,Oy\) lần lượt tại \(x_0,y_0\) thì ta có \(\left(x_0;y_0\right)\) là tọa độ của điểm đó.
2. Để tìm một điểm khi biết tọa độ \(\left(x_0;y_0\right)\) của nó, ta dựng đường vuông góc với \(Ox\) tại \(x_0\), vuông góc với \(Oy\) tại \(y_0\). Hai đường này cắt nhau tại đâu thì đó là vị trí của điểm cần tìm.
3. Một điểm nằm trong góc phần tư thứ \(I\) thì có hoành độ và tung độ đều là các số dương. Một điểm nằm trong góc phần tư thứ \(II\) thì có hoành độ âm, tung độ dương. Một điểm nằm trong góc phần tư thứ \(III\) thì có hoành độ và tung độ đều âm. Một điểm nằm trong góc phần tư thứ \(IV\) thì có hoành độ dương, tung độ âm.
4. Hai điểm đối xứng nhau qua trục hoành thì có hoành độ bằng nhau, tung độ đối nhau. Hai điểm đối xứng nhau qua trục tung thì có tung độ bằng nhau, hoành độ đối nhau. Hai điểm đối xứng nhau qua gốc tọa độ thì có hoành độ và tung độ đều đối nhau.
   @1235889@