Bài 7: Đồ thị hàm số y = ax (a khác 0)
Nội dung lý thuyết
Các phiên bản khác1. Đồ thị hàm số là gì?
Định nghĩa:
Đồ thị hàm số \(y=f\left(x\right)\) là tập hợp tất cả các điểm biểu diễn các cặp giá trị tương ứng \(\left(x;y\right)\) trên mặt phẳng tọa độ
Ví dụ: Cho hàm số \(y=f\left(x\right)\) được cho bởi bảng sau:
| x | -2 | -1 | 0 | 0.5 | 1,5 |
| y | 3 | 2 | -1 | 1 | -2 |
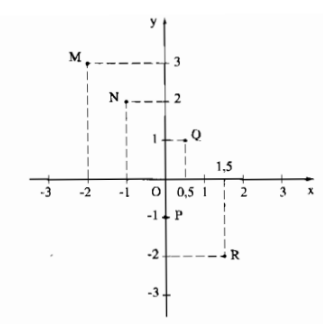
Đố thị hàm số \(y=f\left(x\right)\) trên gồm các điểm M. N. P. Q. R như trong hình sau:
@54389@
2. Đồ thị hàm số \(y=ax\left(a\ne0\right)\)
Ví dụ: Xét hàm số \(y=2x\). Vì x có thể nhận vô số giá trị nên ta không thể liệt kê được hết các cặp số \(\left(x;y\right)\). Ta vẽ một số điểm thuộc đồ thị của nó và qua đó xét xem đồ thị có hình dạng như thế nào.
- Ta thấy các cặp số \(\left(-2;-4\right)\), \(\left(2;4\right)\), \(\left(1;2\right)\), \(\left(-1;-2\right)\), \(\left(0;0\right)\) thỏa mãn hàm số \(y=2x\) và được biểu diễn trên trục tọa độ như sau:
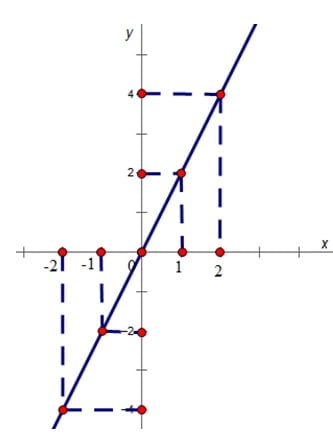
- Vẽ một đường thẳng đi qua 2 điểm \(\left(-2;-4\right)\), \(\left(2;4\right)\) ta thấy đường thẳng đó đi qua các điểm còn lại.
Suy ra: Muốn vẽ được đồ thị của một hàm số \(y=ax\left(a\ne0\right)\) ta cần biết 2 điểm thuộc đồ thị hàm số đó.
@54390@
Xét hàm số \(y=ax\left(a\ne0\right)\), Ta thay cặp số \(\left(x;y\right)=\left(0;0\right)\) vào hàm số thò được: \(0=a.0\) hay \(0=0\) (luôn đúng với mọi \(a\ne0\)). Từ đó ta được nhận xét:
Đồ thị hàm số \(y=ax\left(a\ne0\right)\) là một đường thẳng đi qua gốc tọa độ.
Nhận xét: Vì đồ thị hàm số \(y=ax\left(a\ne0\right)\) là một đường thẳng đi qua gốc tọa độ nên khi vẽ ta chỉ cần xác định thêm một điểm thuộc đồ thị và khác điểm gốc O. Muốn vậy ta cho x một giá trị khác 0 và tìm giá trị tương ứng của y. Cặp giá trị đó là tọa độ của điểm thứ 2.
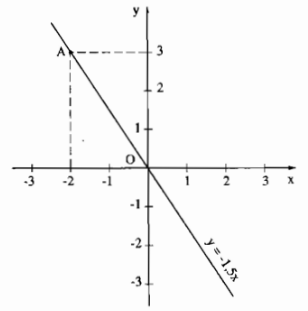
Ví dụ: Vẽ đồ thị hàm số \(y=-1,5x\)?
Vẽ hệ trục tọa độ Oxy. Với \(x=-2\) ta được \(y=3\), Nên điểm \(A\left(-2;3\right)\) thuộc đồ thị hàm số \(y=-1,5x\). Vậy đường thẳng OA là đồ thị của hàm số đã cho.
@54391@