Bài 2: Hệ hai phương trình bậc nhất hai ẩn. Luyện tập
Cho hệ phương trình:\(\left\{{}\begin{matrix}2mx+y=2\\x+2my=4-4m\end{matrix}\right.\)
Tìm các giá trị m nguyên để hệ phương trình có nghiệm duy nhất (x;y) sao cho x và y nguyên
\(\Leftrightarrow\left\{{}\begin{matrix}y=2-2mx\\x+2m\left(2-2mx\right)=4-4m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=2-2mx\\x+4m-4m^2x-4+4m=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=2-2mx\\x\left(1-4m^2\right)=-8m+4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=-2mx+2\\x\left(2m-1\right)\left(2m+1\right)=4\left(2m-1\right)\end{matrix}\right.\)
Nếu m=1/2 thì hệ có vô số nghiệm
Nếu m=-1/2 thì hệ vô nghiệm
Nếu m<>1/2; m<>-1/2 thì hệ có nghiệm duy nhất là:
\(\left\{{}\begin{matrix}x=\dfrac{4}{2m+1}\\y=-2m\cdot\dfrac{4}{2m+1}+2=\dfrac{-8m+4m+2}{2m+1}=\dfrac{-4m+2}{2m+1}\end{matrix}\right.\)
Để x,y nguyên thì \(\left\{{}\begin{matrix}2m+1\inƯ\left(4\right)\\-4m-2+4⋮2m+1\end{matrix}\right.\Leftrightarrow2m+1\inƯ\left(4\right)\)
mà m nguyên
nên \(2m+1\in\left\{1;-1\right\}\)
=>\(m\in\left\{0;-1\right\}\)
Đúng 0
Bình luận (0)
Đề : không cần vẽ hình , hãy cho biết số nghiệm của mỗi hệ phương trình sau đây và giải thích vì sao . Mình cảm ơn rất nhiều ạ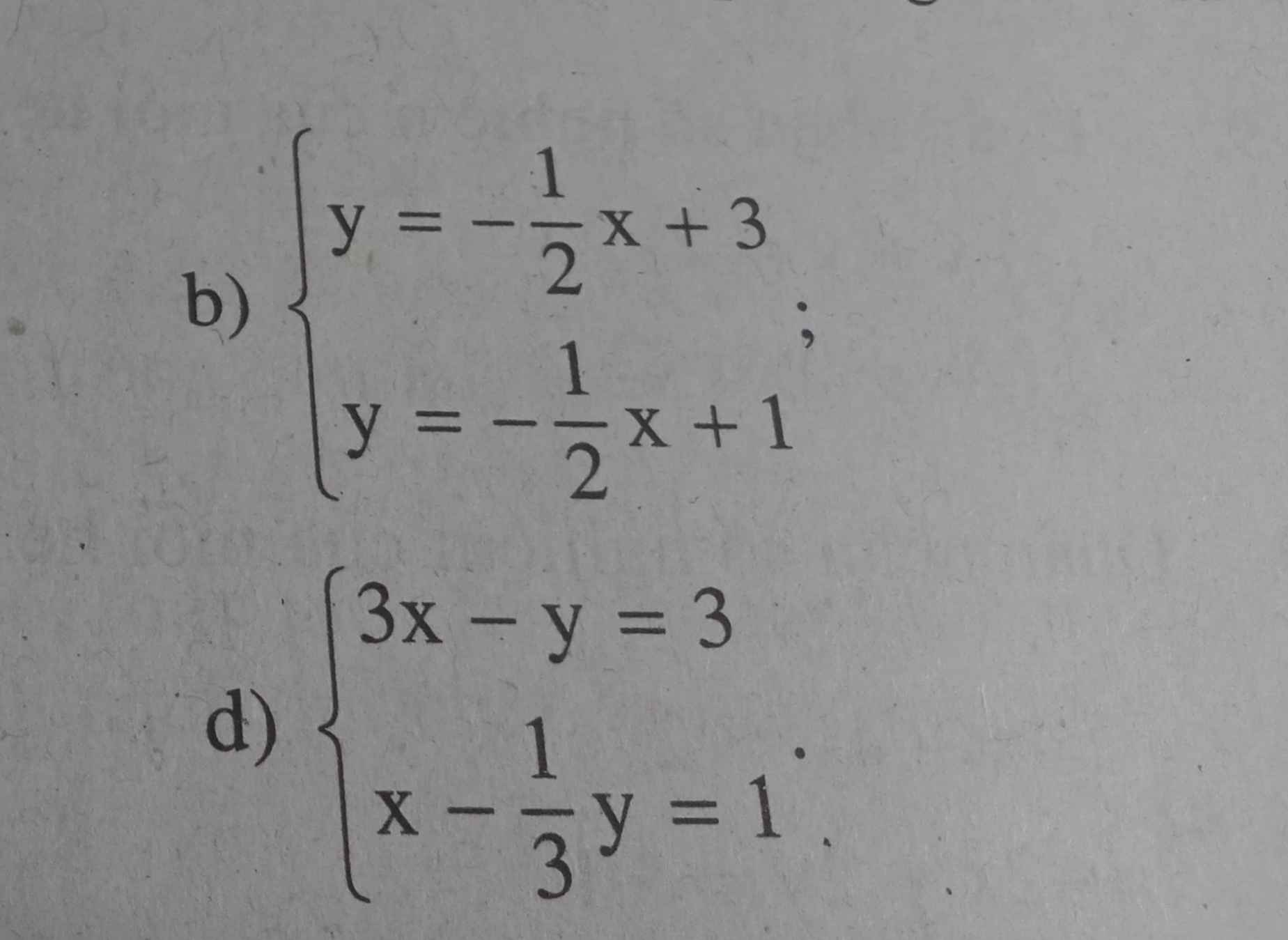
b: \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{-1}{2}x+3=\dfrac{-1}{2}x+1\\y=-\dfrac{1}{2}x+1\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\varnothing\)
d: =>3x-y=3 và 3x-y=3
=>\(\left(x,y\right)\in R\)
Đúng 1
Bình luận (0)
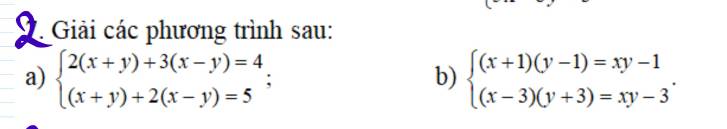
ai giúp mình hai câu này với ạ
Gọi số sản phẩm phải làm theo kế hoạch là \(x\) (sản phẩm)
Theo kế hoạch mỗi ngày cần làm số sản phẩm là \(\dfrac{x}{7}\) (sản phẩm)
Trên thực tế mỗi ngày làm được là \(\dfrac{x}{7}+4\) (sản phẩm)
Tổng số sản phẩm trên thực tế là \(5\left(\dfrac{x}{7}+4\right)\)
Ta có phương trình: \(5\left(\dfrac{x}{7}+4\right)=x+2\)
\(\Rightarrow\dfrac{5}{7}x+20=x+2\Rightarrow\dfrac{2}{7}x=18\Rightarrow x=63\) (sản phẩm)
Đúng 2
Bình luận (0)
Đọc tiếp
\(\Leftrightarrow\sqrt{5}-\sqrt{3x}=8+2\sqrt{15}\)
\(\Leftrightarrow\sqrt{3x}=\sqrt{5}-8-2\sqrt{15}\)
\(\Leftrightarrow x=\dfrac{\left(\sqrt{5}-8-2\sqrt{15}\right)^2}{3}\)
Đúng 0
Bình luận (0)
3x - 4y = 2
⎨5x + 2y = 14
3x - 5y = 4
⎨2x - 10y =5
a: \(\Leftrightarrow\left\{{}\begin{matrix}3x-4y=2\\10x+4y=28\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}13x=30\\3x-4y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{30}{13}\\4y=3x-2=\dfrac{90}{13}-2=\dfrac{54}{26}=\dfrac{27}{13}\end{matrix}\right.\)
=>x=30/13 và y=27/52
b: \(\Leftrightarrow\left\{{}\begin{matrix}6x-10y=8\\2x-10y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x=3\\2x-10y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{4}\\10y=2x-5=\dfrac{3}{2}-5=-\dfrac{7}{2}\end{matrix}\right.\)
=>x=3/4 và y=-7/20
Đúng 2
Bình luận (0)
`{(3x-4y=2), (5x+2y=14):}`
`<=> {(x=30/13), (y=16/13):}`
`{(3x-5y=4), (2x-10y=5):}`
`<=> {(x = 3/4), (y = -7/20):}`
Đúng 1
Bình luận (0)
Giải giúp mik cầu 3 đc hông ạ
Do (d) và (P) cắt nhau, áp dụng phương trình hoành độ giao điểm:
\(x^2=(m-3)x+3m+2\)
\(⇔x^2-(m-3)x-3m-2=0\)
\(△= (m-3)^2-4(-3m-2)\)
\(=m^2+6m+17\)
\(=(m+3)^2+8>0\) với mọi m
Vậy (d) và (P) luôn cắt nhau tại hai điểm phân biệt.
Áp dụng hệ thức Vi-ét:
\(\begin{cases} x_{1}+x_{2}=m-3\\ x_{1}x_{2}=-3m-2 \end{cases}\)
Để (d) và (P) luôn cắt chau tại hai điểm có hoành độ âm:
\(\begin{cases} x_{1}+x_{2}<0\\ x_{1}x_{2}<0 \end{cases}\)\(⇔\begin{cases} m-3<0\\ -3m-2<0 \end{cases}\)\(⇔\begin{cases} m<3\\ m>\dfrac{2}{3} \end{cases}\)
Vậy để (d) và (P) cắt nhau tại hai điểm có hoành độ âm thì \(\dfrac{2}{3} < m <3\)
Đúng 1
Bình luận (0)
g
giúp mình câu giải hệ phương trình được không ạ?
\(\left\{{}\begin{matrix}2x^2+y^2-2y+1=3-y^2\\2x^2+2x+2y^2-3y=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x^2+2y^2-2y=2\\2x^2+2y^2+2x-3y=4\end{matrix}\right.\)
Trừ vế cho vế:
\(2x-y=2\Rightarrow y=2x-2\)
Thế vào \(2x^2+2y^2-2y=2\Leftrightarrow x^2+y^2-y=1\) ta được:
\(x^2+\left(2x-2\right)^2-\left(2x-2\right)=1\)
\(\Leftrightarrow5x^2-10x+5=0\Rightarrow x=1\)
\(\Rightarrow y=0\)
Vậy nghiệm của hệ là: \(\left(x;y\right)=\left(1;0\right)\)
Đúng 1
Bình luận (0)








