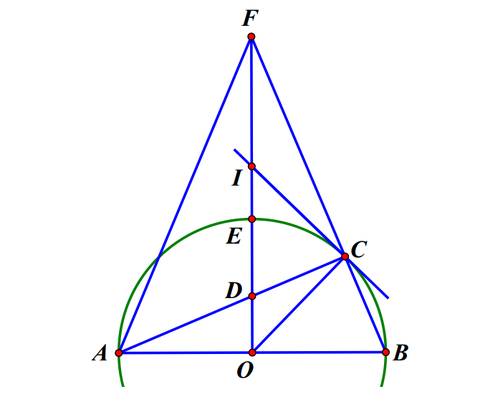
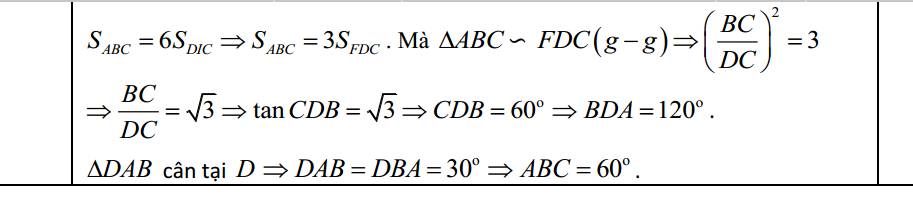Do (d) và (P) cắt nhau, áp dụng phương trình hoành độ giao điểm:
\(x^2=(m-3)x+3m+2\)
\(⇔x^2-(m-3)x-3m-2=0\)
\(△= (m-3)^2-4(-3m-2)\)
\(=m^2+6m+17\)
\(=(m+3)^2+8>0\) với mọi m
Vậy (d) và (P) luôn cắt nhau tại hai điểm phân biệt.
Áp dụng hệ thức Vi-ét:
\(\begin{cases} x_{1}+x_{2}=m-3\\ x_{1}x_{2}=-3m-2 \end{cases}\)
Để (d) và (P) luôn cắt chau tại hai điểm có hoành độ âm:
\(\begin{cases} x_{1}+x_{2}<0\\ x_{1}x_{2}<0 \end{cases}\)\(⇔\begin{cases} m-3<0\\ -3m-2<0 \end{cases}\)\(⇔\begin{cases} m<3\\ m>\dfrac{2}{3} \end{cases}\)
Vậy để (d) và (P) cắt nhau tại hai điểm có hoành độ âm thì \(\dfrac{2}{3} < m <3\)
Đúng 1
Bình luận (0)
