Hãy kiểm tra mỗi cặp số sau có phải là một nghiệm của hệ phương trình tương ứng hay không ?
a) \(\left(-4;5\right)\) \(\left\{{}\begin{matrix}7x-5y=-53\\-2x+9y=53\end{matrix}\right.\)
b) \(\left(3;-11\right)\) \(\left\{{}\begin{matrix}0,2x+1,7=-18,1\\3,2x-y=20,6\end{matrix}\right.\)
c) \(\left(1,5;2\right),\left(3;7\right)\) \(\left\{{}\begin{matrix}10x-3y=9\\-5x+1,5=-4,5\end{matrix}\right.\)
d) \(\left(1;8\right)\) \(\left\{{}\begin{matrix}5x+2y=9\\x-14y=5\end{matrix}\right.\)
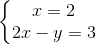 ⇔
⇔ 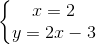
 được B(
được B(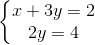 ⇔
⇔ 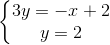 ⇔
⇔ 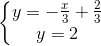
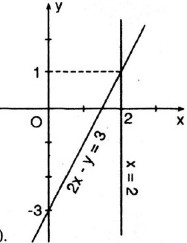
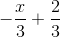 cắt hai trục tọa độ, còn một đồ thị là đường thẳng y = 2 song song vơi trục hoành.
cắt hai trục tọa độ, còn một đồ thị là đường thẳng y = 2 song song vơi trục hoành.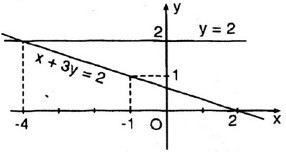
 được A(0;
được A(0; 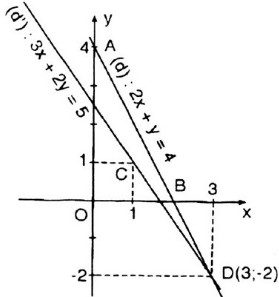
 được C(0;
được C(0;  được D(
được D(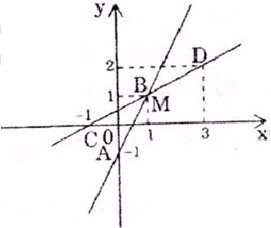
a) với x=-4 ;y=5 thay vào hệ phương trình ta có
(1) 7.(-4)-5.5=53
<=>-53=-53(đúng)
(2) -2.(-4) + 9.5=53
<=> 53=53(đúng)
vậy (-4;5) là nghiệm của hệ phương trình
các ý a),b),c) ,d) làm tương tự
Trả lời bởi Quỳnh Phạm