
Bài 2: Hàm số bậc nhất.
3:
a: Vì a=-4<0
nên hàm số nghịch biến
b: \(f\left(0\right)=-4\cdot0+2=2\)
\(f\left(2\right)=-4\cdot2+2=-6\)
\(f\left(2-\sqrt{3}\right)=-8+4\sqrt{3}+2=4\sqrt{3}-6\)
\(f\left(4-3\sqrt{2}\right)=-16+12\sqrt{2}+2=12\sqrt{2}-14\)
c: -4x+2=-2
=>-4x=-4
=>x=1
-4x+2=4
=>-4x=2
=>x=-1/2
Đúng 0
Bình luận (0)
Tìm m để hàm số sau là hàm số bậc nhất
a. y=\(\left(5m-2\right)x+m\)
b.\(y=\left(3m-5\right)x+8-m\)
c.\(y=\dfrac{4m-3}{2}x+m-1\)
d.\(y=\left(2m-3\right)x+7-m\)
`a)` H/s là h/s bậc nhất `<=>5m-2 \ne 0<=>m \ne 2/5`
`b)` H/s là h/s bậc nhất `<=>3m-5 \ne 0<=>m \ne 5/3`
`c)` H/s là h/s bậc nhất `<=>[4m-3]/2 \ne 0<=>4m-3 \ne 0<=>m \ne 3/4`
`d)` H/s là h/s bậc nhất `<=>2m-3 \ne 0<=>m \ne 3/2`
Đúng 1
Bình luận (0)
Cho đường thẳng d: y = (m+2)x + m với m là tham số và m ≠ -2
a) Tìm điểm cố định mà d luôn đi qua được với mọi m
b) Tìm m để d cắt Ox, Oy tại A và B sao cho diện tích tam giác OAB bằng \(\dfrac{1}{2}\)
THANKS ALL <3
a: y=mx+m+2x=m(x+1)+2x
Điểm M có tọa độ là:
x+1=0 và y=2x
=>x=-1 và y=-2
b: tọa độ A là;
y=0 và (m+2)x+m=0
=>A(-m/m+2;0)
tọa độ B là;
x=0 và y=m
=>B(0;m)
=>OA=|m/m+2|, OB=|m|
theo đề, ta có: OA*OB=1
=>m^2=|m+2|
TH1: m>=-2
=>m^2=m+2
=>m^2-m-2=0
=>m=2 hoặc m=-1
TH2: m<-2
=>m^2+m+2=0(loại)
Đúng 0
Bình luận (0)
một người có độ cao từ mắt đến chân là 1,6m. Anh ấy đứng thẳng và cách xa cây dừa 2,4m và đưa mắt nhìn theo hai tia chứa cạnh góc vuông của một ê kê đến gốc và ngọn của cây dừa. Tính được chiều cao của cây dừa (làm tròn đến chữ số thập phân thứ ba)?
Ai giúp mình với ạ, cảm ơn nhiều.
Xét tứ giác AHMC có \(\widehat{A}=\widehat{H}=\widehat{C}=90^o\)
=> AHMC là hình chữ nhật
\(=>AH=CM=1,6m;AC=HM=2,4m\)
Asp dụng hệ thức lượng trong ΔABM vuông tại M, đường cao MH có
\(MH^2=HA.HB< =>HB=\dfrac{MH^2}{HA}=\dfrac{2,4^2}{1,6}=3,6m\)
Chiều cao của cây dừa đó là \(AB=AH+BH=1,6+3,6=5,2m\)
Đúng 4
Bình luận (0)
Tìm m để hàm số y = f(x) = \(\sqrt{x-1}+mx+2\) (với m là tham số) thỏa mãn
\(f\left(5-2\sqrt{3}\right)\) = \(f\left(2\right)\)
\(f\left(5-2\sqrt{3}\right)=f\left(2\right)\)
\(\Leftrightarrow\sqrt{4-2\sqrt{3}}+\left(5-2\sqrt{3}\right)m+2=\sqrt{1}+2m+2\)
\(\Leftrightarrow\sqrt{\left(\sqrt{3}-1\right)^2}+\left(5-2\sqrt{3}\right)m-2m=1\)
\(\Leftrightarrow\sqrt{3}-1+\left(3-2\sqrt{3}\right)m=1\)
\(\Leftrightarrow\left(3-2\sqrt{3}\right)m=2-\sqrt{3}\)
\(\Leftrightarrow m=\dfrac{2-\sqrt{3}}{3-2\sqrt{3}}=-\dfrac{\sqrt{3}}{3}\)
Đúng 2
Bình luận (1)
Tìm m để hàm số f(x) = \(\sqrt{x+1}\) + mx + 2 (với m là tham số) thỏa mãn
\(f\left(6+4\sqrt{3}\right)\) = f(2)
\(f\left(6+4\sqrt{3}\right)=f\left(2\right)\)
\(\Leftrightarrow\sqrt{7+4\sqrt{3}}+\left(6+4\sqrt{3}\right)m+2=\sqrt{3}+2m+2\)
\(\Leftrightarrow\sqrt{\left(2+\sqrt{3}\right)^2}+\left(6+4\sqrt{3}\right)m-2m=\sqrt{3}\)
\(\Leftrightarrow2+\sqrt{3}+\left(4+4\sqrt{3}\right)m=\sqrt{3}\)
\(\Leftrightarrow\left(2+2\sqrt{3}\right)m=-1\)
\(\Rightarrow m=-\dfrac{1}{2+2\sqrt{3}}=\dfrac{1-\sqrt{3}}{4}\)
Đúng 1
Bình luận (0)
Tìm m để hàm số y = f(x) = \(\sqrt{x-1}\) + mx + 2 (với m là tham số) thỏa mãn f \(\left(5-2\sqrt{3}\right)\) + f(2)
y=m2x2+m(x+2-4x2)+1-2x gia tri m de thanh ham bac nhat
\(y=\left(m^2-4m\right)x^2+\left(m-2\right)x+2m+1\)
Hàm là hàm bậc nhất khi:
\(\left\{{}\begin{matrix}m^2-4m=0\\m-2\ne0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m=0\\m=4\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Tìm trên mặt phẳng tọa độ tất cả các điểm:
a,Có tung độ bằng 5.
b,Có hoành độ bằng 2.
c,Có tung độ bằng 0.
d,Có hoành độ bằng 0.
e,Có hoành độ và tung độ bằng nhau.
f,Có hoành độ và tung độ đối nhau.
a: A(x;5)
b: B(2;y)
c: C(x;0)
d: D(0;y)
e: E(x;x)
f: F(x;-x)
Đúng 0
Bình luận (0)
Làm hộ 1B thôi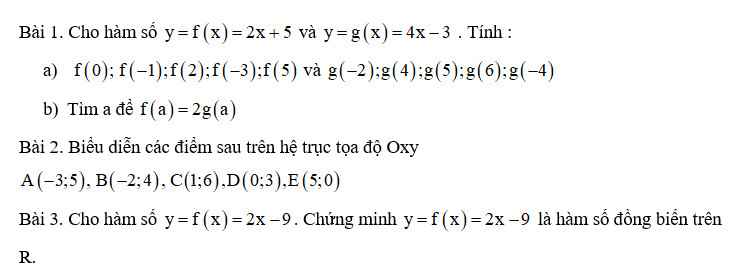
\(f\left(a\right)=2g\left(a\right)\Leftrightarrow2a+5=2\left(4a-3\right)\)
\(\Leftrightarrow2a+5=8a-6\)
\(\Leftrightarrow6a=11\)
\(\Rightarrow a=\dfrac{11}{6}\)
Đúng 1
Bình luận (0)




