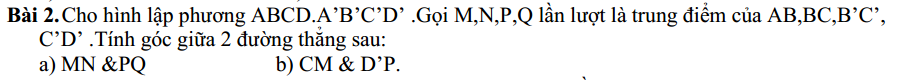Bài 2: Hai đường thẳng vuông góc
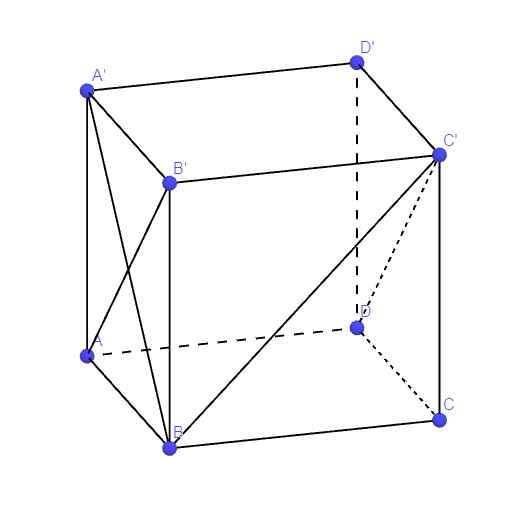
a.
P là trung điểm B'C', Q là trung diểm C'D'
\(\Rightarrow PQ\) là đường trung bình tam giác B'C'D'
\(\Rightarrow PQ||B'D'\Rightarrow PQ||BD\)
\(\Rightarrow\widehat{\left(MN;PQ\right)}=\widehat{\left(MN;BD\right)}\)
Lại có MN là đường trung bình tam giác ABC \(\Rightarrow MN||AC\)
Mà \(AC\perp BD\Rightarrow MN\perp BD\)
\(\Rightarrow\widehat{\left(MN;PQ\right)}=90^0\)
b.
\(D'P||DN\Rightarrow\widehat{\left(CM;D'P\right)}=\widehat{\left(CM;DN\right)}\)
Ta có:
\(\overrightarrow{CM}=\overrightarrow{CB}+\overrightarrow{BM}=\overrightarrow{CB}+\dfrac{1}{2}\overrightarrow{BA}\)
\(\overrightarrow{DN}=\overrightarrow{DC}+\overrightarrow{CN}=-\overrightarrow{BA}+\dfrac{1}{2}\overrightarrow{CB}\)
\(\Rightarrow\overrightarrow{CM}.\overrightarrow{DN}=\left(\overrightarrow{CB}+\dfrac{1}{2}\overrightarrow{BA}\right)\left(-\overrightarrow{BA}+\dfrac{1}{2}\overrightarrow{CB}\right)\)
\(=-\overrightarrow{CB}.\overrightarrow{BA}+\dfrac{1}{2}CB^2-\dfrac{1}{2}BA^2+\dfrac{1}{4}\overrightarrow{BA}.\overrightarrow{CB}\)
\(=\dfrac{1}{2}CB^2-\dfrac{1}{2}BA^2=0\)
\(\Rightarrow CM\perp DN\)
\(\Rightarrow\widehat{\left(CM;D'P\right)}=90^0\)
Đúng 0
Bình luận (0)
a. Do ABCD.A'B'C'D' là hình lập phương
\(\Rightarrow C'D||AB'\)
\(\Rightarrow\) Góc giữa A'B và C'D bằng góc giữa A'B và AB'
Mà \(A'B\perp AB'\) (hai đường chéo hình vuông)
\(\Rightarrow\widehat{\left(A'B;C'D\right)}=90^0\)
b.
Do \(AD'||BC'\) (t/c lập phương)
\(\Rightarrow\widehat{\left(A'B;AD'\right)}=\widehat{\left(A'B;BC'\right)}=\widehat{A'BC'}\)
Mà \(A'B=BC'=A'C'=a\sqrt{2}\) (với a là cạnh lập phương)
\(\Rightarrow\Delta A'BC'\) đều
\(\Rightarrow\widehat{A'BC'}=60^0\)
Đúng 0
Bình luận (0)
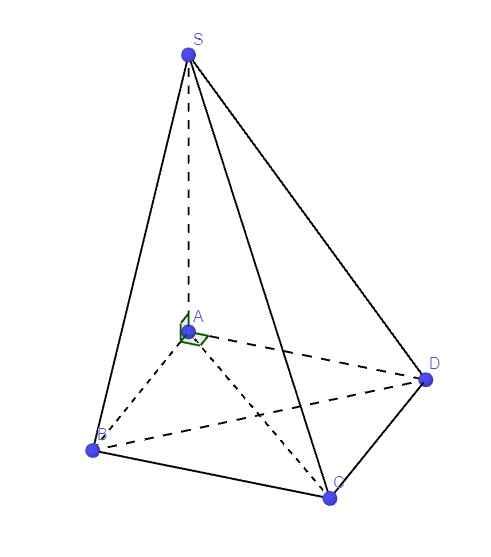
Cho hình chóp S. ABCD có đáy là hình vuông góc với đáy ABCD. Tính góc giữa 2 mặt phẳng SAB và SAD
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp AD\\AB\perp AD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow AD\perp\left(SAB\right)\)
Mà \(AD\in\left(SAD\right)\)
\(\Rightarrow\left(SAD\right)\perp\left(SAB\right)\)
\(\Rightarrow\) Góc giữa (SAB) và (SAD) là \(90^0\)
Đúng 0
Bình luận (0)
Câu 11 : \(CM\cap\left(ABCD\right)=C\)
Thấy : SA \(\perp\left(ABCD\right)\) ; từ M kẻ MH // SA ( H \(\in AD\) ) => H là hình chiếu của M trên (ABCD) \(\Rightarrow\left(CM;\left(ABCD\right)\right)=\widehat{MCH}\)
Ta có : \(MH=\dfrac{1}{2}SA=\sqrt{2}a\)
Tam giác HDC vuông tại D : \(HC=\sqrt{HD^2+DC^2}=\sqrt{a^2+a^2}=\sqrt{2}a\)
Tam giác MHC vuông tại H : \(tan\widehat{MCH}=\dfrac{MH}{HC}=\dfrac{\sqrt{2}a}{\sqrt{2}a}=1\)
\(\Rightarrow\widehat{MCH}=45^o\) \(\Rightarrow\left(CM;\left(ABCD\right)\right)=45^o\)
Chọn A
Đúng 1
Bình luận (0)
Cho hình chố SABC, có đáy ABC là tam giác vuông cân tại B, SA vuông (ABC). Gọi M là trung điểm của AC.
a, Chứng minh rằng (SBM) vuông (SAC)
b, Gọi H,K lần lượt kaf hình chiếu của A lên AB. CmR (AHK) vuông (SBC)
Bạn xem lại đề câu b giúp mình nha, vì hình chiếu của A không thể lên cạnh AB được và hai điểm H,K là hình chiếu của A không thể lên 1 cạnh được á
Đúng 0
Bình luận (0)
Giúp e chi tiết câu 24 đi ạ
Theo tính chất hình lập phương, ta có:
\(C'D'\perp\left(BB'C'C\right)\Rightarrow C'D'\perp BC'\)
\(\Rightarrow\widehat{\left(C'D';BC'\right)}=90^0\)
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD đáy là hình vuông có cạnh 2a. Cạnh SA=a và vuông góc với đáy. Gọi M là trung điểm của CD. Tính cos α với α là góc tạo bởi 2 đường thắng SB, AM.
Bạn vẽ hình giúp mình nha ^^
Xét (ABCD), kẻ \(MH\perp AB\left(H\in AB\right)\)
Xét (SAB), kẻ HF//SB(\(F\in SA\))
Có: \(\left\{{}\begin{matrix}MH\perp AB\\MH\perp SA\end{matrix}\right.\)\(\Rightarrow MH\perp\left(SAB\right)\)\(\Rightarrow MH\perp HF\)
Ta có: \(\alpha=\left(\stackrel\frown{SB,AM}\right)=\left(\stackrel\frown{HF,MH}\right)=arccos\left(\dfrac{HA}{HF}\right)\)
Xét \(\Delta AHF\) vuông tại A có: \(HF^2=HA^2+AF^2=a^2+\left(\dfrac{a}{2}\right)^2=\dfrac{5}{4}a^2\Rightarrow HF=\dfrac{a\sqrt{5}}{2}\)
\(\Rightarrow\alpha=arccos\left(\dfrac{HA}{HF}\right)=arccos\left(\dfrac{2a}{a\sqrt{5}}\right)\approx26,57^o\) \(\Rightarrow cos\alpha=\dfrac{HA}{HF}=\dfrac{2a}{a\sqrt{5}}=\dfrac{2}{\sqrt{5}}\)
Đúng 3
Bình luận (2)
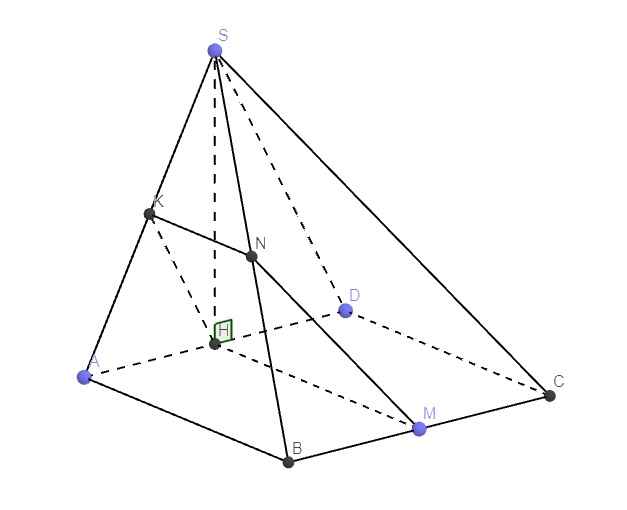
Bài 1 : cho hình chóp SABCD có đáy ABCD là hình vuông và SH vuông góc với mặt phẳng ( ABCD ) tại trung điểm H của cạnh AD . a, CM tam giác SCD vuôngb, Gọi M,K là trung điểm BC , SA . Chứng minh ( SCD ) song song ( HKM )c, ( HKM ) cắt SB tại N . Chứng minh HKMN là hình thang vuôngBài 2 : cho hình chóp SABCD đáy là hình vuông và SM vuông với ( ABCD ) với M là trung điểm AD .a, CM : tam giác SAB và tam giác SCD vuôngb, Gọi N là trung điểm CD , CM AN vuông góc với ( SMB)giúp mình với nha , cảm ơn nh...
Đọc tiếp
Bài 1 : cho hình chóp SABCD có đáy ABCD là hình vuông và SH vuông góc với mặt phẳng ( ABCD ) tại trung điểm H của cạnh AD .
a, CM tam giác SCD vuông
b, Gọi M,K là trung điểm BC , SA . Chứng minh ( SCD ) song song ( HKM )
c, ( HKM ) cắt SB tại N . Chứng minh HKMN là hình thang vuông
Bài 2 : cho hình chóp SABCD đáy là hình vuông và SM vuông với ( ABCD ) với M là trung điểm AD .
a, CM : tam giác SAB và tam giác SCD vuông
b, Gọi N là trung điểm CD , CM AN vuông góc với ( SMB)
giúp mình với nha , cảm ơn nhiều ạ
1.
a.
\(\left\{{}\begin{matrix}SH\perp\left(ABCD\right)\Rightarrow SH\perp CD\\AD\perp CD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
\(\Rightarrow CD\perp SD\Rightarrow\Delta SCD\) vuông tại D
b.
Do H là trung điểm AD, K là trung điểm SA
\(\Rightarrow KH\) là đường trung bình tam giác SAD
\(\Rightarrow KH||SD\Rightarrow KH||\left(SCD\right)\)
H là trung điểm AD, M là trung điểm BC \(\Rightarrow HM||CD\)
\(\Rightarrow HM||\left(SCD\right)\)
Mà HM cắt KH tại H
\(\Rightarrow\left(HKM\right)||\left(SCD\right)\)
c.
Qua K kẻ đường thẳng song song AB cắt SB tại N
\(\Rightarrow N=\left(HKM\right)\cap SB\)
\(\left\{{}\begin{matrix}KN||AB\\HM||AB\end{matrix}\right.\) \(\Rightarrow KN||HM\) (1)
Mặt khác \(\left\{{}\begin{matrix}HM||CD\\CD||\left(SAD\right)\end{matrix}\right.\) \(\Rightarrow HM\perp\left(SAD\right)\Rightarrow HM\perp KH\) (2)
(1);(2) \(\Rightarrow\) HKNM là hình thang vuông
Đúng 2
Bình luận (1)
2.
a.
Ta có: \(\left\{{}\begin{matrix}SM\perp\left(ABCD\right)\Rightarrow SM\perp AB\\AB\perp AD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow AB\perp\left(SAD\right)\)
\(\Rightarrow AB\perp SA\)
\(\Rightarrow\Delta SAB\) vuông tại A
Lại có \(\left\{{}\begin{matrix}CD||AB\\AB\perp\left(SAD\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\Rightarrow CD\perp SD\)
\(\Rightarrow\Delta SCD\) vuông tại D
b.
Ta có: \(\overrightarrow{AN}.\overrightarrow{BM}=\left(\overrightarrow{AD}+\overrightarrow{DN}\right)\left(\overrightarrow{BA}+\overrightarrow{AM}\right)=\left(\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{AB}\right)\left(-\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}\right)\)
\(=-\overrightarrow{AD}.\overrightarrow{AB}+\dfrac{1}{2}AD^2-\dfrac{1}{2}AB^2+\dfrac{1}{4}\overrightarrow{AB}.\overrightarrow{AD}=0\)
\(\Rightarrow AN\perp BM\) (1)
Mà \(SM\perp\left(ABCD\right)\Rightarrow SM\perp AN\) (2)
(1);(2) \(\Rightarrow AN\perp\left(SMB\right)\)
Đúng 2
Bình luận (0)
Xem thêm câu trả lời