Bài 3: Đường thẳng vuông góc với mặt phẳng
Nội dung lý thuyết
Các phiên bản khácI. ĐỊNH NGHĨA
Đường thẳng \(d\) được gọi là vuông góc với mặt phẳng \(\left(\alpha\right)\) nếu \(d\) vuông góc với mọi đường thẳng \(a\) nằm trong mặt phẳng \(\left(\alpha\right)\).

Khi \(d\) vuông góc với \(\left(\alpha\right)\) ta còn nói \(\left(\alpha\right)\) vuông góc với \(d\), hoặc \(d\) và \(\left(\alpha\right)\) vuông góc với nhau và kí hiệu là \(d\perp\left(\alpha\right)\).
II. ĐIỀU KIỆN ĐỂ ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG
Định lí:
Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau cùng thuộc một mặt phẳng thì nó vuông góc với mặt phẳng ấy.
Hệ quả:
Nếu một đường thẳng vuông góc với hai cạnh của tam giác thì nó cũng vuông góc với cạnh thứ ba của tam giác đó.
@62265@
III. TÍNH CHẤT
Tính chất 1:
Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.

Mặt phẳng trung trực của một đoạn thẳng:
Người ta gọi mặt phẳng đi qua trung điểm \(I\) của đoạn thẳng \(AB\) và vuông góc với đường thẳng \(AB\) là mặt phẳng trung trực của đoạn thẳng \(AB\).
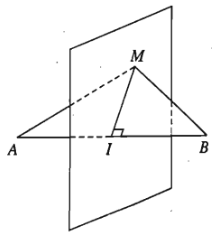
Tính chất 2:
Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.

IV. LIÊN HỆ GIỮA QUAN HỆ SONG SONG VÀ QUAN HỆ VUÔNG GÓC CỦA ĐƯỜNG THẲNG VÀ MẶT PHẲNG
Tính chất 1:
a) Cho hai đường thẳng song song. Mặt phẳng nào vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.
b) Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì song song với nhau.
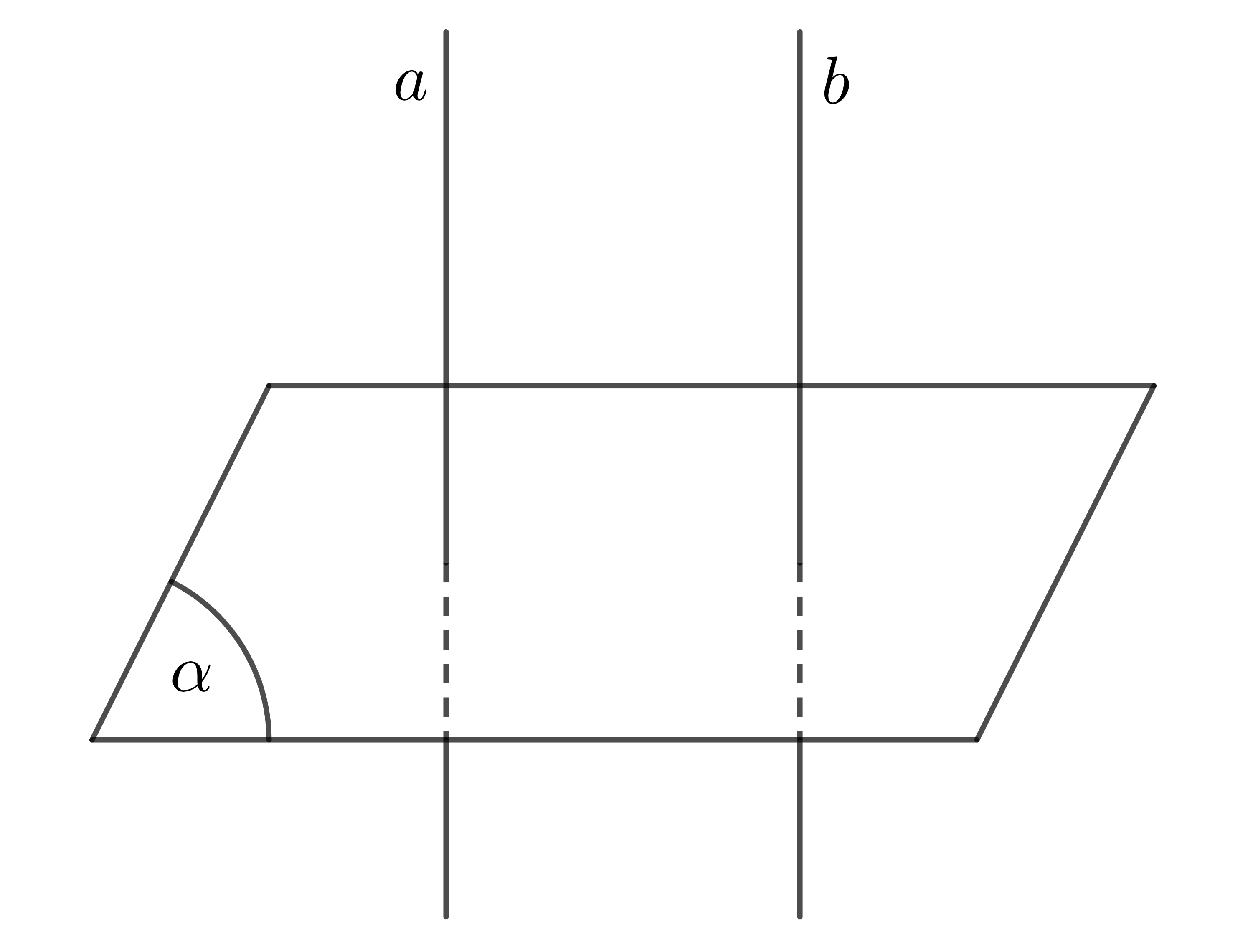
Tính chất 2:
a) Cho hai mặt phẳng song song. Đường thẳng nào vuông góc với mặt phẳng này thì cũng vuông góc với mặt phẳng kia.
b) Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì hai mặt phẳng đó song song.
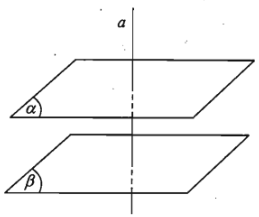
Tính chất 3:
a) Cho đường thẳng \(a\) và mặt phẳng \(\left(\alpha\right)\) song song với nhau. Đường thẳng nào vuông góc với \(\left(\alpha\right)\) thì cũng vuông góc với \(a\).
b) Nếu một đường thẳng và một mặt phẳng (không chứa đường thẳng đó) cùng vuông góc với một đường thẳng khác thì song song với nhau.

Ví dụ 1: Cho hình chóp \(S.ABC\) có đáy là tam giác \(ABC\) vuông tại \(B\) và có cạnh \(SA\) vuông góc với mặt phẳng \(\left(ABC\right)\).
a) Chứng minh \(BC\perp\left(SAB\right)\) ;
b) Gọi \(AH\) là đường cao của tam giác \(SAB\). Chứng minh \(AH\perp SC\).
Giải:
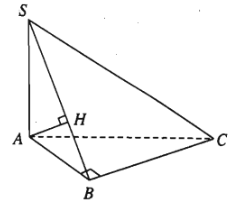
a) Vì \(SA\perp\left(ABC\right)\) nên \(SA\perp BC\)
Ta có: \(BC\perp SA\), \(BC\perp AB\) nên suy ra \(BC\perp\left(SAB\right)\).
b) Vì \(BC\perp\left(SAB\right)\) và \(AH\) nằm trong \(\left(SAB\right)\) nên \(AH\perp BC\)
Ta có: \(AH\perp BC\), \(AH\perp SB\) nên suy ra \(AH\perp\left(SBC\right)\)
Từ đó suy ra \(AH\perp SC\).
@62249@
V. PHÉP CHIẾU VUÔNG GÓC VÀ ĐỊNH LÍ BA ĐƯỜNG VUÔNG GÓC
1. Phép chiếu vuông góc
Cho đường thẳng \(\Delta\) vuông góc với mặt phẳng \(\left(\alpha\right)\). Phép chiếu song song theo phương của \(\Delta\) lên mặt phẳng \(\left(\alpha\right)\) được gọi phép chiếu vuông góc lên mặt phẳng \(\left(\alpha\right)\).
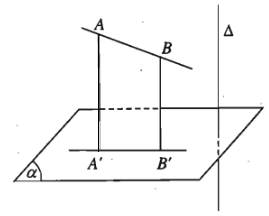
2. Định lí ba đường thẳng vuông góc
Cho đường thẳng \(a\) nằm trong mặt phẳng \(\left(\alpha\right)\) và \(b\) là đường thẳng không thuộc \(\left(\alpha\right)\) đồng thời không vuông góc với \(\left(\alpha\right)\). Gọi \(b'\) là hình chiếu vuông góc của \(b\) lên \(\left(\alpha\right)\). Khi đó \(a\) vuông góc với \(b\) khi và chỉ khi \(a\) vuông góc với \(b'\).
3. Góc giữa đường thẳng và mặt phẳng
Cho đường thẳng \(d\) và mặt phẳng \(\left(\alpha\right)\).
Trường hợp đường thẳng \(d\) vuông góc với mặt phẳng \(\left(\alpha\right)\) thì ta nói góc giữa đường thẳng \(d\) và mặt phẳng \(\left(\alpha\right)\) bằng \(90^0\).
Trường hợp đường thẳng \(d\) không vuông góc với mặt phẳng \(\left(\alpha\right)\) thì góc giữa \(d\) và hình chiếu \(d'\) của nó trên \(\left(\alpha\right)\) được gọi là góc giữa đường thẳng \(d\) và mặt phẳng \(\left(\alpha\right)\).
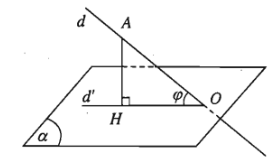
Chú ý: Nếu \(\varphi\) là góc giữa đường thẳng \(d\) và mặt phẳng \(\left(\alpha\right)\) thì ta luôn có \(0^0\le\varphi\le90^0\).
Ví dụ 2: Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), cạnh \(SA=a\sqrt{2}\) và \(SA\perp\left(ABCD\right)\).
a) Gọi \(M,N\) lần lượt là hình chiếu của \(A\) lên các đường thẳng \(SB,SD\). Tính góc giữa \(SC\) và \(\left(AMN\right)\).
b) Tính góc giữa \(SC\) và \(\left(ABCD\right)\).
Giải:

a) Ta có \(BC\perp AB\), \(BC\perp SA\) suy ra \(BC\perp\left(SAB\right)\) \(\Rightarrow\) \(BC\perp AM\)
mà \(SB\perp AM\) suy ra \(AM\perp\left(SBC\right)\) nên \(AM\perp SC\)
Tương tự ta chứng minh được \(AN\perp SC\)
Suy ra \(SC\perp\left(AMN\right)\). Vậy góc giữa \(SC\) và \(\left(AMN\right)\) là \(90^0\)
b) Do \(AC\) là hình chiếu của \(SC\) lên \(\left(ABCD\right)\) nên \(\widehat{SCA}\) là góc giữa \(SC\) và \(\left(ABCD\right)\)
Tam giác \(SAC\) cân tại \(A\) có \(AS=AC=a\sqrt{2}\). Do đó \(\widehat{SCA}=45^0\).
@62256@
Danh sách các phiên bản khác của bài học này. Xem hướng dẫn