Bài 2: Cực trị hàm số

y'=x^2-(m+4)x-(2m^2-5m-3)

Để f(x) có 2 cực trị x1,x2 thì y'=0 có 2 nghiệm phân biệt

=>(m+4)^2+4(2m^2-5m-3)>0

=>m^2+8m+16+8m^2-20m-12>0

=>9m^2-12m+4>0

=>m<>2/3

x1,x2 là 2 cạnh liên tiếp của 1 hình chữ nhật

=>x1*x2>0 và x1+x2>0

=>m+4>0 và -(2m^2-5m-3)>0

=>m>-4 và -1/2<m<3

=>-1/2<m<3 và m<>2/3

Bình phương Độ dài đường chéo là:

l^2=x1^2+x2^2

=(x1+x2)^2-2x1x2

=(m+4)^2+2(2m^2-5m-3)

=m^2+8m+16+4m^2-10m-6

=5m^2-2m+10

=5(m^2-2/5m+2)

=5(m^2-2*m*1/5+1/25+49/25)

=5(m-1/5)^2+49/5>=49/5

Dấu = xảy ra khi m=1/5

=>l^2 min=49/5

=>m=1/5

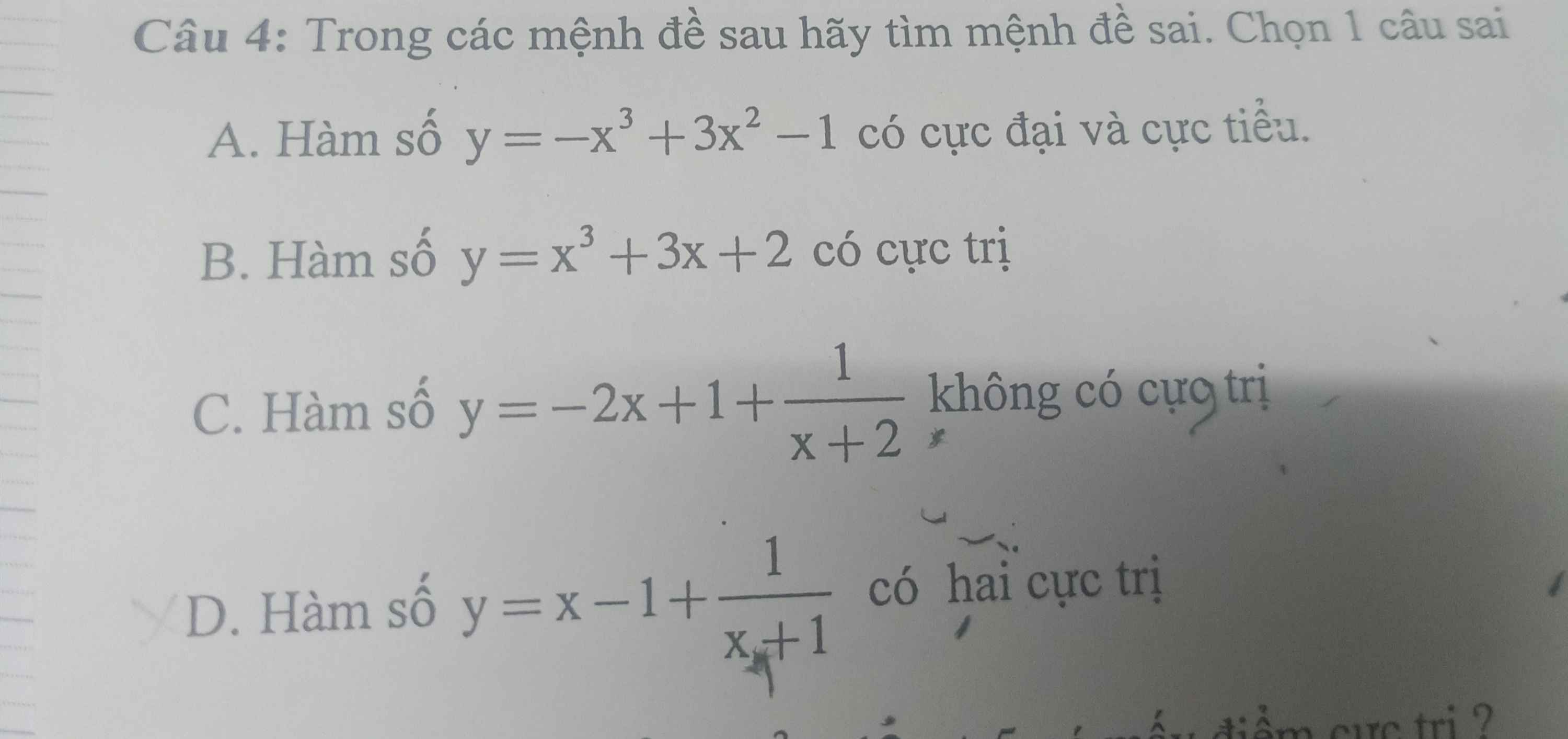
B là mệnh đề sai

\(y=x^3+3x+2\Rightarrow y'=3x^2+3>0;\forall x\)

\(\Rightarrow\) Hàm không có cực trị

\(y'=x^2+2mx+m+6\)

Tiến hành chia y cho y' và lấy phần dư ta được pt đường thẳng qua 2 cực trị của hàm là:

\(y=\dfrac{-2m^2+2m+12}{3}x-\left(\dfrac{1}{3}m^2+4m+1\right)\)

\(y'=3x^2+6x+m-1\)

Hàm có 2 cực trị khi: \(\Delta'=9-3\left(m-1\right)>0\Rightarrow m< 4\)

Tiến hành chia y cho y' và lấy phần dư ta được đường thẳng đi qua 2 cực trị có dạng:

\(y=\dfrac{2m-8}{3}x+\dfrac{2m+1}{3}\)

Giao điểm với các trục: \(A\left(0;\dfrac{2m+1}{3}\right)\) ; \(B\left(-\dfrac{2m+1}{2m-8};0\right)\)

\(\Rightarrow\dfrac{1}{2}\left|\dfrac{2m+1}{3}\right|.\left|\dfrac{2m+1}{2m-8}\right|=16\)

\(\Rightarrow\left(2m+1\right)^2-96\left(8-2m\right)=0\)

\(\Rightarrow...\)

\(y'=3x^2-6mx=0\Rightarrow\left[{}\begin{matrix}x=0\Rightarrow y=4m^3\\x=2m\Rightarrow y=0\end{matrix}\right.\) với \(m\ne0\)

CĐ, CT đối xứng qua \(y=x\) khi:

\(4m^3=2m\Rightarrow m^2=\dfrac{1}{2}\Rightarrow m=\pm\dfrac{\sqrt{2}}{2}\)

b.

\(y'=x^2-2mx-1\) có \(ac< 0\) nên luôn có 2 cực trị

Gọi \(x_{1;}x_2\) là hoành độ 2 cực trị \(\Rightarrow\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=-1\end{matrix}\right.\)

\(y_1-y_2=\dfrac{1}{3}\left(x_1^3-x_2^3\right)-m\left(x_1^2-x_2^2\right)-\left(x_1-x_2\right)\)

\(=\dfrac{1}{3}\left(x_1-x_2\right)\left[\left(x_1+x_2\right)^2-x_1x_2\right]-m\left(x_1-x_2\right)\left(x_1+x_2\right)-\left(x_1-x_2\right)\)

\(=\dfrac{1}{3}\left(x_1-x_2\right)\left(4m^2+1\right)-2m^2\left(x_1-x_2\right)-\left(x_1-x_2\right)\)

\(=-\dfrac{2}{3}\left(m^2+1\right)\left(x_1-x_2\right)\)

\(\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2-4x_1x_2=4\left(m^2+1\right)\)

Khoảng cách 2 cực trị:

\(f=\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2}=\sqrt{\left(x_1-x_2\right)^2+\dfrac{4}{9}\left(m^4+2m^2+1\right)\left(x_1-x_2\right)^2}\)

\(=\sqrt{4\left(m^2+1\right)+\dfrac{16}{9}\left(m^2+1\right)^3}\ge\sqrt{4+\dfrac{16}{9}}\)

Dấu "=" xảy ra khi \(m=0\)

Ta có : \(y=x^3-\left(m+6\right)x^2+\left(2m+9\right)x-2\left(C_m\right)\)

PTHĐGĐ của \(C_m\) với Ox : \(x^3-\left(m+6\right)x^2+\left(2m+9\right)x-2=0\)  (1) 

\(\Leftrightarrow\left(x-2\right)\left[x^2-\left(m+4\right)x+1\right]=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x^2-\left(m+4\right)x+1=0\left(2\right)\end{matrix}\right.\)

(Cm) có 2 điểm cực trị nằm về 2 phía của Ox \(\Leftrightarrow\) (1) có 3 no p/b 

\(\Leftrightarrow\left(2\right)\) có 2 no p/b \(\ne2\)

\(\Leftrightarrow\left\{{}\begin{matrix}\Delta=\left(m+4\right)^2-4>0\\g\left(2\right)\ne0\end{matrix}\right.\)   \(\Leftrightarrow\left\{{}\begin{matrix}\left(m+2\right)\left(m+6\right)>0\\2^2-2\left(m+4\right)+1\ne0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m< -6\\m>-2\end{matrix}\right.\\m\ne-\dfrac{3}{2}\end{matrix}\right.\)  \(\Leftrightarrow\left\{{}\begin{matrix}m\ne-\dfrac{3}{2}\\m>-2\end{matrix}\right.\)

Vậy ...