Bài 2: Cực trị hàm số
Tìm tất cả các giá trị của tham số m để đồ thị hàm số y= \(x^3-3mx^2+3mx+m\) có hai điểm cực trị và hai điểm đó cách đều đường thẳng x=2
Tìm tất cả các giá trị của tham số m để đồ thị hàm số y= \(x^3-3mx^2+3mx+m\) có hai điểm cực trị và hai điểm đó cách đều đường thẳng x=2
cho hàm số y=f(x)=\(-x^3+3x^2-3mx+3m-4\). Tìm m để hàm số có hai điểm cực trị lớn hơn m
\(y'=-3x^2+6x-3m=3\left(-x^2+2x-m\right)\)
H/s có 2 điểm cực trị nên : \(y'=0\) có 2 no p/b \(\Leftrightarrow-x^2+2x-m\) có 2 no p/b \(\Leftrightarrow\Delta'>0\) \(\Leftrightarrow1-m>0\Leftrightarrow m< 1\)
Viet : \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=m\end{matrix}\right.\)
H/s có 2 điểm cực trị > m nên : \(\left\{{}\begin{matrix}2>2m\\\left[{}\begin{matrix}m>m^2;m>0\\m< m^2;m< 0\end{matrix}\right.\end{matrix}\right.\)
Sau đấy bn giải ra
Đúng 2
Bình luận (0)
Cho hàm số y= \(\dfrac{x^2-2kx+k^2+1}{x-k}\) với tham số k. Chứng minh với mọi k đồ thị luôn có cực đại, cực tiểu và tổng tung độ của chúng bằng 0
1, Tìm tổng tất cả các giá trị thực tham số m sao cho đương thẳng đi qua 2 điểm cực trị của hàm số \(y=2x\text{^3+3(m-1)x^2+6m(1-2m)x}\) song song đường thẳng \(y=-4x\)
A.\(m=-\dfrac{1}{3}\) B. \(m=\dfrac{2}{3}\) C. \(m=-\dfrac{2}{3}\) D.m=1
Cho hàm số y= \(\dfrac{x^2-2kx+k^2+1}{x-k}\) với tham số k. Chứng minh với mọi k đồ thị luôn có cực đại, cực tiểu và tổng tung độ của chúng bằng 0
cho hàm số y=f(x)=\(-x^3+3x^2-3mx+3m-4\). Tìm m để hàm số có hai điểm cực trị lớn hơn m
cho hàm số y=\(\dfrac{x^2-x+m}{x+1}\) . Xác định m sao cho hàm số:
a, Có cực trị
b, Có hai cực trị và hai giá trị cực trị trái dấu nhau
Giải giúp mình câu 16-19 với ạ :<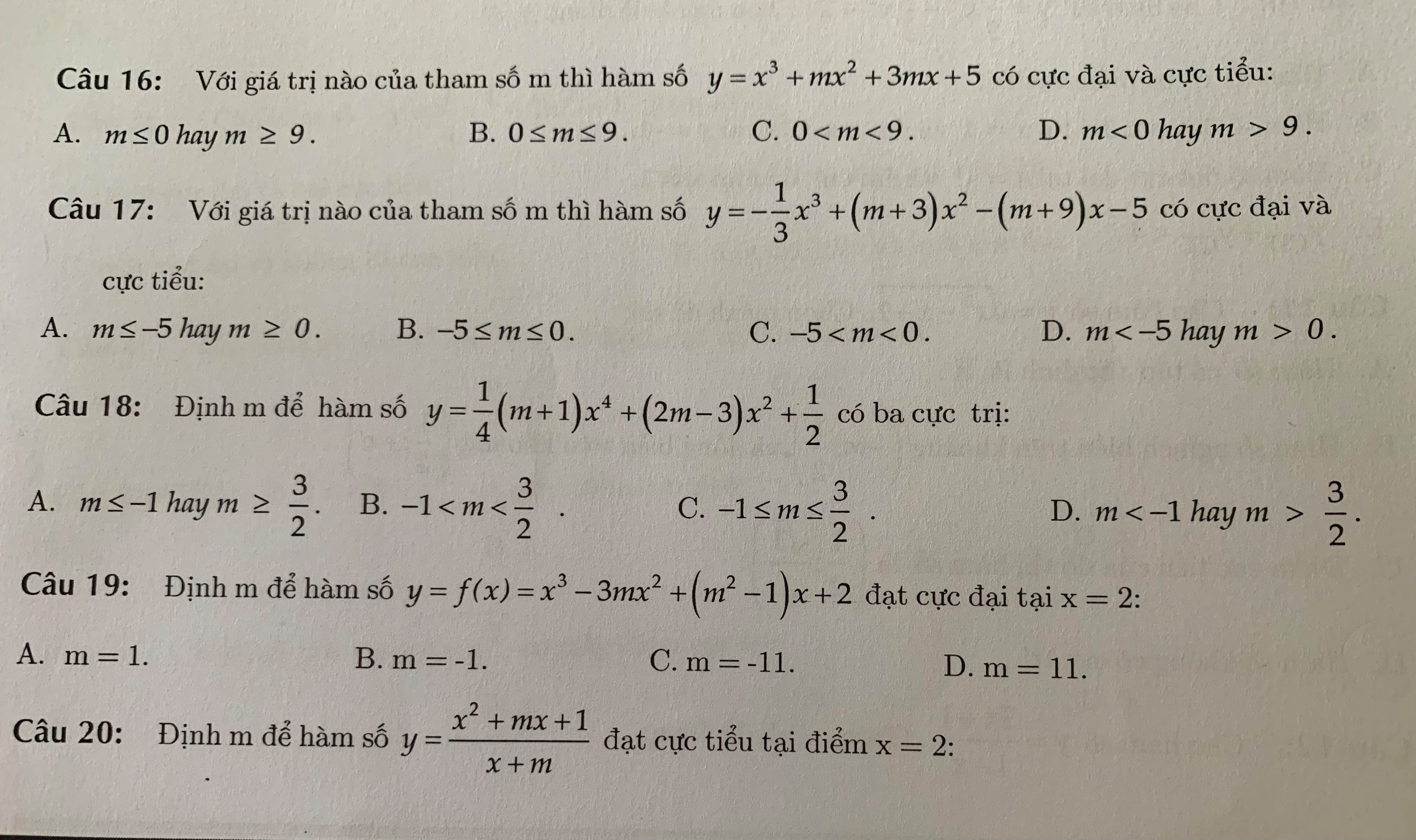
16. giải rồi nha
19. \(y'=3x^2-6mx+m^2-1\), \(y'\left(2\right)=m^2-12m+11=0\Leftrightarrow\left[{}\begin{matrix}m=1\\m=11\end{matrix}\right.\)
Với m = 1 => \(y'=3x^2-6x=0\)\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=0\end{matrix}\right.\)
Vẽ BBT ra nhé chị ko có tools để vẽ, thấy x=2 là cực tiểu => loại
Với m =11 => \(y'=3x^2-66x+120=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=20\end{matrix}\right.\)
Vẽ BBT thấy x=2 là cực đại => tm
D.
Đúng 1
Bình luận (0)



