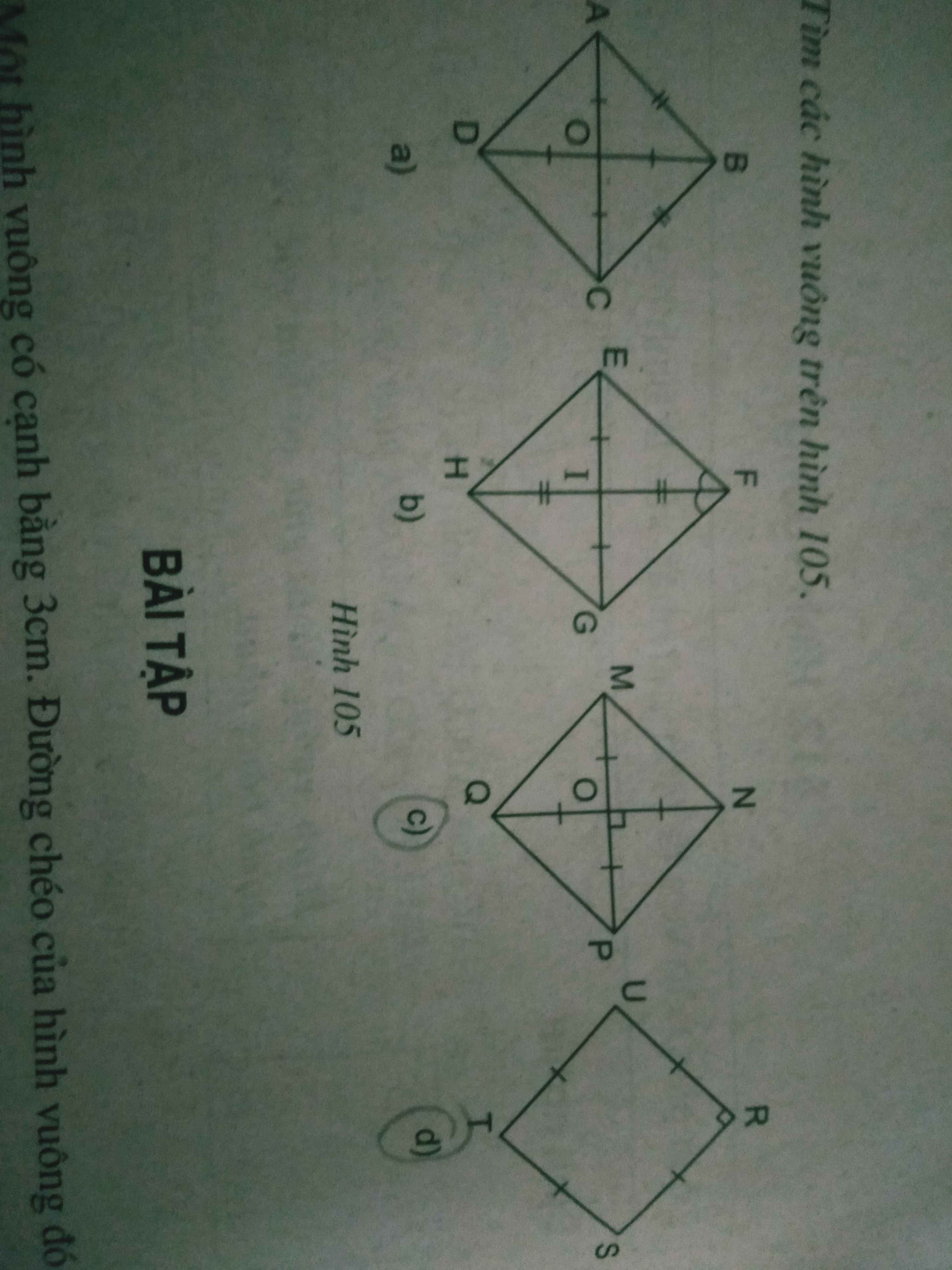
Cho hình vuông ABCD có cạnh bằng a, trên các cạnh AB, AD lần lượt lấy hai điểm M,N sao cho tam giác AMN có chu vi bằng 2a. Tìm vị trí của M, N để diện tích tam giác CMN lớn nhất.
Bài 12: Hình vuông
Đặt AM=x; AN=y
MN^2=AM^2+AN^2
=>\(MN=\sqrt{x^2+y^2}\)
\(P_{AMN}=AM+AN+MN=x+y+\sqrt{x^2+y^2}=2a\)
và x+y>=2*căn xy; \(\sqrt{x^2+y^2}>=\sqrt{2xy}\)
=>\(2a=x+y+\sqrt{x^2+y^2}>=2\sqrt{xy}+\sqrt{2xy}\)
=>\(2a>=\sqrt{xy}\left(2+\sqrt{2}\right)\)
=>\(\sqrt{xy}< =\dfrac{2a}{2+\sqrt{2}}\)
=>\(S_{AMN}=\dfrac{1}{2}xy< =\dfrac{1}{2}\cdot\left(\dfrac{2a}{2+\sqrt{2}}\right)^2=\left(3-2\sqrt{2}\right)a^2\)
Dấu = xảy ra khi \(x=y=\left(2-\sqrt{2}\right)a\)
Đúng 1
Bình luận (0)
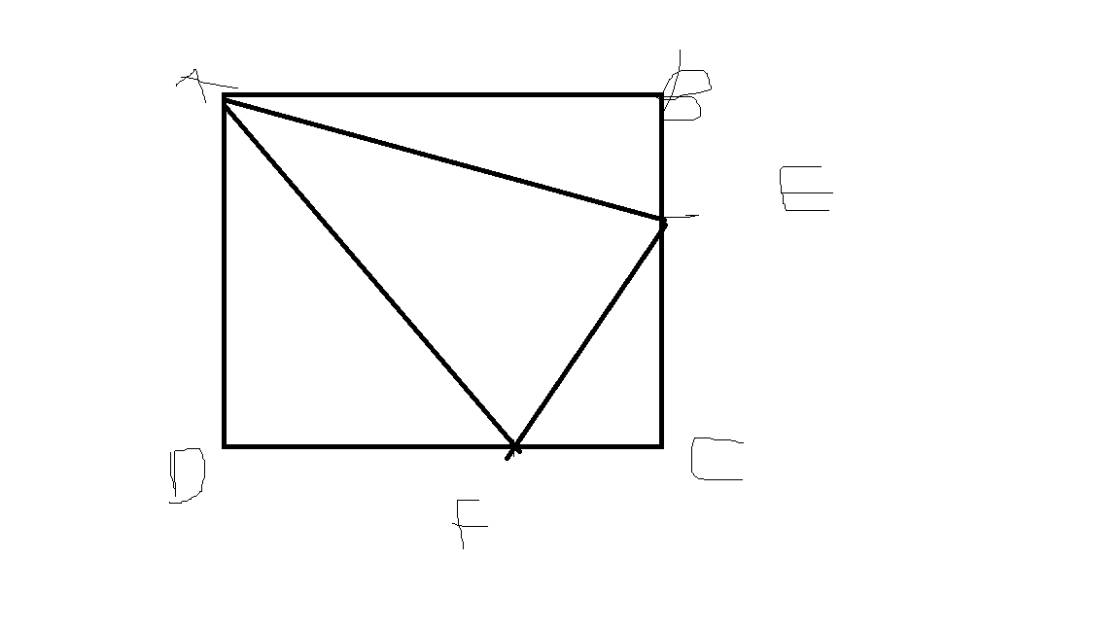
Cho hình vuông ABCD. trên tia đối của tia ba lấy điểm E. đường thẳng EC cắt AD tại F, AC cắt BF tại O. chứng minh EO đi qua trung điểm của AF
Cho tam giác ABC có AB = 8cm AC = 12cm
Trên cạnh AB lấy điểm D sao cho BD = 2cm trên cạnh AC lấy điểm E sao cho AE = 9cm.
Chứng minh AADE đồng dạng A ABC.
Xét ΔADE và ΔABC có
AD/AB=AE/AC
góc A chung
=>ΔADE đồng dạng với ΔABC
Đúng 0
Bình luận (0)
Một mảnh đất hình vuông có độ dài hai cạnh là a và b. Hãy tính diện tích của mảnh đất nói trên.
Giúp mình với ạ :)
Cho hình vuông ABCD hãy dựng điểm E thuộc cạnh BC điểm F thuộc cạnh CD sao cho tam giác AEF là tam giác đều.
Câu 4: Cho hình vuông ABCD, M thuộc đường chéo AC. Gọi E,F theo thứ tự là hình chiếu của M trên AD, CD. Chứng minh rằng:
a. BM vuông góc EF
b. Các đường thẳng BM, EF, CE đồng quy.
Một mảnh đất hình vuông có cạnh là 70m. Tính số thóc thu hoạch được của mảnh đất. Biết cứ 100m² thu hoạch được 90kg thoc6
Diện tích là 70^2=4900m2
Khối lượng thóc thu được là 4900:100*90=4410kg
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A. Đường cao AH.kẻ HD vuông góc với AB tại D ,kẻ HE vuông góc với AC tại E a, C/m tứ giác ADHE là hình chữ nhật b, C/m AH=DE ? c, tam giác ABC cần có điều kiện gì thì tứ giác ADHE là hình vuông Viết GT, KL
a: Xét tứ giác ADHE có
góc ADH=góc AEH=góc DAE=90 độ
nên ADHE là hình chữ nhật
b: Vì ADHE là hình chữ nhật
nên AH=DE
c: Để ADHE là hình vuông thì AH là phân giác của góc DAE
mà AH vuông góc vơi BC
nên ΔABC cân tại A
=>AB=AC
Đúng 1
Bình luận (0)
Cho hình vuông ABCD có cạnh bằng a, điểm E thuộc cạnh CD, điểm F thuộc cạnh BC sao cho góc EAF 45 độ. Gọi H là chân đường vuông góc kẻ từ A đến EF. Gọi G, I theo thứ tự là giao điểm của BD với AF, AE.1. CMR:a, EH ED, FB FHb, BG2 + DI2 GI22. Gọi M là giao điểm của AH và BD. Kẻ MP vuông góc với DC, MQ vuông góc với BC ( P thuộc CD, Q thuộc BC). Xác định vị trí điểm M để tam giác APQ có diện tích nhỏ nhất
Đọc tiếp
Cho hình vuông ABCD có cạnh bằng a, điểm E thuộc cạnh CD, điểm F thuộc cạnh BC sao cho góc EAF = 45 độ. Gọi H là chân đường vuông góc kẻ từ A đến EF. Gọi G, I theo thứ tự là giao điểm của BD với AF, AE.
1. CMR:
a, EH = ED, FB = FH
b, BG2 + DI2 = GI2
2. Gọi M là giao điểm của AH và BD. Kẻ MP vuông góc với DC, MQ vuông góc với BC ( P thuộc CD, Q thuộc BC). Xác định vị trí điểm M để tam giác APQ có diện tích nhỏ nhất
Hình a và hình b thì ko đủ dữ kiện để chứng minh
Hình c: Xét tứ giác NMQP có
O là trung điểm chung của NQ và MP
NQ=MP
NQ vuông góc MP
=>NMQP là hìnhvuông
Hình d: Xét tứ giác SRUT có
SR=RU=UT=TS
góc R=90 độ
=>SRUT là hình vuông
Đúng 0
Bình luận (0)