Cho đường tròn tâm O đường kính AB; trên nửa đường tròn lấy điểm C sao cho AC>AB, qua C dựng đường thẳng vuông góc với OC cắt đường thẳng AB tại D. Kẻ CH vuông góc với AB (H thuộc AB), kẻ BK vuông góc với CD ( K thuộc CD); đường kính CH cắt đường thẳng BK tại E. a) Chứng minh 4 điểm C,H,B,K cùng thuộc 1 đường tròn. b) Cm KH//AC. c) Cm BH.AD=AH.BD
Bài 1: Sự xác định đường tròn. Tính chất đối xứng của đường tròn
a: Ta có: \(\widehat{CHB}=90^0\)
=>ΔCHB vuông tại H
=>ΔCHB nội tiếp đường tròn đường kính CB(4)
Ta có: \(\widehat{CKB}=90^0\)
=>ΔCKB vuông tại K
=>ΔCKB nội tiếp đường tròn đường kính CB(5)
Từ (4) và (5) suy ra C,H,B,K cùng thuộc đường tròn đường kính CB
b:
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
Ta có: \(\widehat{OCB}+\widehat{BCK}=\widehat{OCK}=90^0\)
\(\widehat{OCB}+\widehat{OCA}=\widehat{BCA}=90^0\)
Do đó: \(\widehat{BCK}=\widehat{OCA}\)(1)
Ta có: CHBK là tứ giác nội tiếp
=>\(\widehat{BCK}=\widehat{BHK}\left(2\right)\)
Xét ΔOAC có OC=OA
nên ΔOAC cân tại O
=>\(\widehat{OAC}=\widehat{OCA}\)(3)
Từ (1),(2),(3) suy ra \(\widehat{BHK}=\widehat{OAC}\)
mà hai góc này là hai góc ở vị trí đồng vị
nên HK//AC
Đúng 1
Bình luận (0)
vẽ hộ hình giúp mình với phần a) Cm 2 tam giác nội tiếp
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn vẽ đường tròn tâm O đường kính BC cắt tại AB và AC lần lượt tại D và E. Gọi H là giao điểm của BE và CD chứng minh H là trực tâm của tam giác ABC Từ đó suy ra AH vuông góc với BC
Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
=>CD\(\perp\)DB tại D
=>CD\(\perp\)AB tại D
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
=>BE\(\perp\)EC tại E
=>BE\(\perp\)AC tại E
Xét ΔABC có
BE,CD là đường cao
BE cắt CD tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC
Đúng 1
Bình luận (0)
tam giác ABC vuông ở A có AB = 5cm , AC =12cm .Bán kính đường tròn ngoại tiếp tam giác đó bằng
Xem chi tiết
\(\Delta ABC\) vuông tại A
\(\Rightarrow BC^2=AB^2+AC^2\) (Pytago)
\(=5^2+12^2\)
\(=169\)
\(\Rightarrow BC=13\left(cm\right)\)
Gọi R là bán kính cần tìm
\(\Rightarrow\) Bán kính đường tròn ngoại tiếp \(\Delta ABC\):
\(R=\dfrac{BC}{2}=\dfrac{13}{2}=6,5\left(cm\right)\)
Đúng 1
Bình luận (0)
cho nửa đường tròn (O) có đường kính AB . M là điểm nằm bên ngoài đường tròn sao cho MA , MB cắt nửa đường tròn lần lượt tại N , P a) chứng mính BN ⊥ MA , AP ⊥ MB b) Gọi K là giao điểm của BN và AP . Chứng minh MK ⊥ AB
Đọc tiếp
cho nửa đường tròn (O) có đường kính AB . M là điểm nằm bên ngoài đường tròn sao cho MA , MB cắt nửa đường tròn lần lượt tại N , P a) chứng mính BN ⊥ MA , AP ⊥ MB b) Gọi K là giao điểm của BN và AP . Chứng minh MK ⊥ AB
a: Xét (O) có
ΔANB nội tiếp
AB là đường kính
Do đó: ΔANB vuông tại N
=>BN\(\perp\)AM
Xét (O) có
ΔAPB nội tiếp
AB là đường kính
Do đó: ΔAPB vuông tại P
=>AP\(\perp\)MB
b: Xét ΔMAB có
AP,BN là các đường cao
AP cắt BN tại K
Do đó: K là trực tâm của ΔMAB
=>MK\(\perp\)AB
Đúng 1
Bình luận (0)
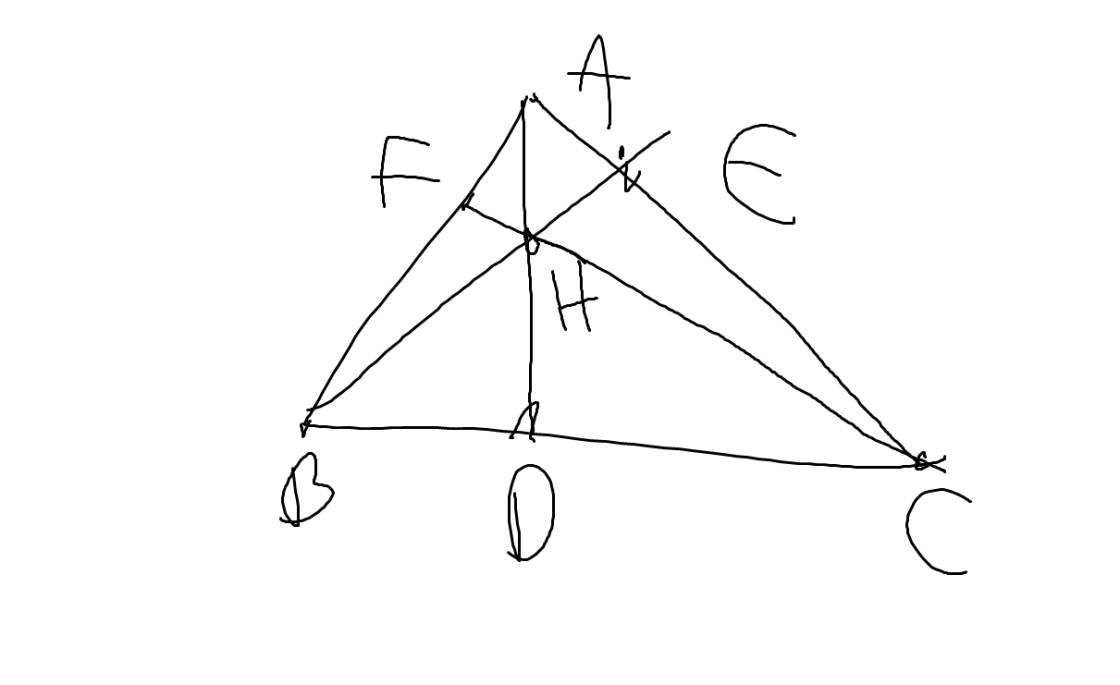
cho Tam giác nhọn ABC, kẻ các đường cao AD,BÉ,CF Cm:4 điểm thuộc một đường tròn: 1) A,F,D,C 2)A,E,D,B 3) gọi H là giải điểm của 3 đường cao Cm: A,F,H,E 4) E,H,D,C 5) E,H,D,B (Vẽ thêm hình càng tốt ạ)
1: Xét tứ giác AFDC có
\(\widehat{AFC}=\widehat{ADC}=90^0\)
nên AFDC là tứ giác nội tiếp
2: Xét tứ giác AEDB có
\(\widehat{AEB}=\widehat{ADB}=90^0\)
nên AEDB là tứ giác nội tiếp
3:
Xét tứ giác AFHE có
\(\widehat{AFH}+\widehat{AEH}=90^0+90^0=180^0\)
=>AEHF là tứ giác nội tiếp
4: Xét tứ giác HECD có
\(\widehat{HEC}+\widehat{HDC}=90^0+90^0=180^0\)
=>HECD là tứ giác nội tiếp
Đúng 2
Bình luận (2)
Cm:4 điểm thuộc một đường tròn: 1) A,F,D,C 2)A,E,D,B 3) gọi H là giải điểm của 3 đường cao Cm: A,F,H,E 4) E,H,D,C 5) E,H,D,B (Vẽ thêm hình càng tốt ạ)
Bạn ghi đầy đủ đề đi bạn
Đúng 0
Bình luận (0)
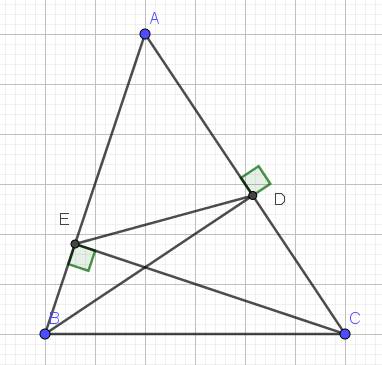
Cho tam giác ABC đường cao BD và CE A) gọi y là giao điểm của BD và CE. Chứng minh 4 điểm BD CE cùng nằm trên 1 đường tròn
Lời giải:
Xét tứ giác $BEDC$ có:
$\widehat{BEC}=\widehat{BDC}=90^0$. Mà 2 góc này cùng nhìn cạnh $BC$ nên $BEDC$ là tứ giác nội tiếp.
$\Rightarrow B,C,E,D$ cùng nằm trên 1 đường tròn.
Đúng 0
Bình luận (0)
Cho ABC vuông tại A, đường cao AH. Vẽ đường tròn (I) có đường kính HB cắt
cạnh AB tại D. Vẽ đường tròn (K) đường kính HC cắt AC tại E.
a) Chứng minh tứ giác ADHE là hình chữ nhật.
b) Chứng minh AD.AB AE.AC .
c) Cho AB 3cm,BC 5cm . Tính DE và diện tích tứ giác DEKI.
a: Xét (I) có
ΔHDB nội tiếp
HB là đường kính
Do đó: ΔHDB vuông tại D
=>HD\(\perp\)AB
Xét (K) có
ΔCEH nội tiếp
CH là đường kính
Do đó: ΔCEH vuông tại E
=>HE\(\perp\)AC
Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
=>ADHE là hình chữ nhật
b: Xét ΔHAB vuông tại H có HD là đường cao
nên \(AD\cdot AB=AH^2\left(1\right)\)
Xét ΔHAC vuông tại H có HE là đường cao
nên \(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AD\cdot AB=AE\cdot AC\)
c: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=5^2-3^2=16\)
=>AC=4(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot5=3\cdot4=12\)
=>AH=2,4(cm)
ADHE là hình chữ nhật
=>AH=DE=2,4(cm)
\(\widehat{EDI}=\widehat{EDH}+\widehat{IDH}\)
\(=\widehat{HAC}+\widehat{IHD}\)
\(=\widehat{HAC}+\widehat{HCA}=90^0\)
=>ED\(\perp\)DI
\(\widehat{KED}=\widehat{KEH}+\widehat{DEH}\)
\(=\widehat{KHE}+\widehat{HAB}\)
\(=\widehat{HAB}+\widehat{HBA}=90^0\)
=>EK\(\perp\)ED
mà ED\(\perp\)DI
nên EK//DI
Xét tứ giác EDIK có
EK//DI
ED\(\perp\)EK
Do đó: EDIK là hình thang vuông
\(DI+EK=\dfrac{1}{2}HB+\dfrac{1}{2}HC=\dfrac{1}{2}\cdot\left(HB+HC\right)=2,5\left(cm\right)\)
\(S_{EDIK}=\dfrac{1}{2}\cdot ED\cdot\left(EK+DI\right)\)
\(=\dfrac{1}{2}\cdot2,4\cdot2,5=3\left(cm^2\right)\)
Đúng 0
Bình luận (0)
Cho ABC vuông tại A, Biết AB 6cm, AC 8cm . Vẽ đường tròn O đường kính
AB cắt BC tại H.
a) Tính AH, CH.
b) Kẻ OK AH tại K và tia OK cắt AC tại D. Chứng minh DH OH
a: Xét (O) có
ΔAHB nội tiếp
AB là đường kính
Do đó: ΔAHB vuông tại H
=>AH\(\perp\)BC tại H
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=100\)
=>\(BC=\sqrt{100}=10\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AH\cdot BC=AB\cdot AC\\CA^2=CH\cdot CB\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AH=\dfrac{6\cdot8}{10}=4,8\left(cm\right)\\CH=\dfrac{8^2}{10}=6,4\left(cm\right)\end{matrix}\right.\)
b: ΔOAH cân tại O
mà OK là đường cao
nên OK là phân giác của \(\widehat{AOH}\)
Xét ΔOAD và ΔOHD có
OA=OH
\(\widehat{AOD}=\widehat{HOD}\)
OD chung
Do đó: ΔOAD=ΔOHD
=>\(\widehat{OAD}=\widehat{OHD}=90^0\)
=>HD\(\perp\)HO
Đúng 1
Bình luận (0)
tam giác ABC vuông tại A, M là trung điểm BC
a)Chứng minh A,B,C thuộc đường tròn (M)
b)Biết AB=6cm, AC=8cm.Tính bán kình đường tròn ngoại tiếp tam giác ABC
a: ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MB=MC
=>ΔABC nội tiếp (M)
b: ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
ΔABC vuông tại A có AM là đường trung tuyến
nên \(AM=\dfrac{BC}{2}=5\left(cm\right)\)
=>R=5cm
Đúng 1
Bình luận (0)


