Lời giải:
Xét tứ giác $BEDC$ có:
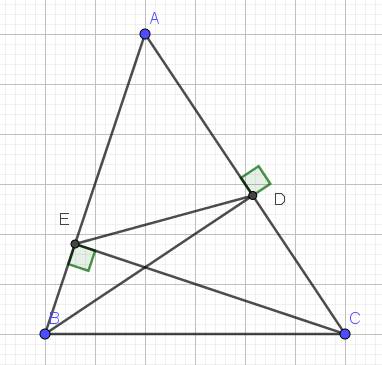
$\widehat{BEC}=\widehat{BDC}=90^0$. Mà 2 góc này cùng nhìn cạnh $BC$ nên $BEDC$ là tứ giác nội tiếp.
$\Rightarrow B,C,E,D$ cùng nằm trên 1 đường tròn.
Lời giải:
Xét tứ giác $BEDC$ có:
$\widehat{BEC}=\widehat{BDC}=90^0$. Mà 2 góc này cùng nhìn cạnh $BC$ nên $BEDC$ là tứ giác nội tiếp.
$\Rightarrow B,C,E,D$ cùng nằm trên 1 đường tròn.

Cho tam giác ABC, các đường cao BD và CE. Gọi N là trực tâm của tam giác. Chứng minh 4 điểm A,E,N,D cùng thuôc một đường tròn
Cho tam giác đều ABC cạnh bằng 6cm, hai đường cao BD và CE. Gọi G là giao điểm của BD và CE.
Chứng minh bốn điểm A, E,D, G cùng thuộc một đường tròn. Xác định tâm và tính bán kính R của đườg tròn
này.
Cho tam giác ABC, các đường cao BD và CE. M là trung điểm BC. Chứng minh rằng A không nằm trong đường tròn tâm M.
Cho tam giác ABC, các đường cao BD và CE cắt nhau tại I. Chứng minh A, D, E, I cùng thuộc một đường tròn
cho tam giác ABC đều, 2 đường cao BD và CE.
a) Chứng minh 4 điểm B,C,D,E cùng thuộc 1 đường tròn
b) Gọi G là giao điểm của BD và CE. Chứng minh 4 điểm A,E,D,G cùng thuộc 1 đường tròn. Tính bán kính, biết tam giác ABC có cạnh = 8
cho tam giác abc . đường cao bd cắt ce tài h . chứng minh : 4 điểm a,d,h,e thuộc 1 đường tròn
Cho tam giác ABC , đường cao BD , CE . Chứng minh 4 điểm E , B, D , C cùng thuộc 1 đường tròn .
1) cho hình thoi ABCD có góc C=60°. gọi D là giao điểm AC và BD. Gọi E,F,G,H lần lượt là trung điểm AB,BC,CD,DA. Chứng minh rằng các điểm E,B,F,G,D,H cùng nằm trên một đường tròn
cho hình thoi ABCD có góc C=60°. gọi D là giao điểm AC và BD. Gọi E,F,G,H lần lượt là trung điểm AB,BC,CD,DA. Chứng minh rằng các điểm E,B,F,G,D,H cùng nằm trên một đường tròn