Bài 1: Hàm số lượng giác

\(y=-sin^2x-cosx+2 \\=cos^2x-cosx+1=(cosx-\dfrac{1}{2})^2+\dfrac{3}{4}\ge\dfrac{3}{4} \\Đẳng\ thức\ xảy\ ra\ khi\ x=\dfrac{\pi}{3}+2k\pi\ (k\ nguyên) \\Vậy\ Miny=\dfrac{3}{4}\ (khi\ x=\dfrac{\pi}{3}+2k\pi\ (k\ nguyên)) \\y=-sin^2x-cosx+2 \\=cos^2x-cosx+1\le1-(-1)+1=3 \\Đẳng\ thức\ xảy\ ra\ khi\ x=\pi+2k\pi\ (k\ nguyên) \\Vậy\ Maxy=3\ (khi\ x=\pi+2k\pi\ (k\ nguyên)).\)

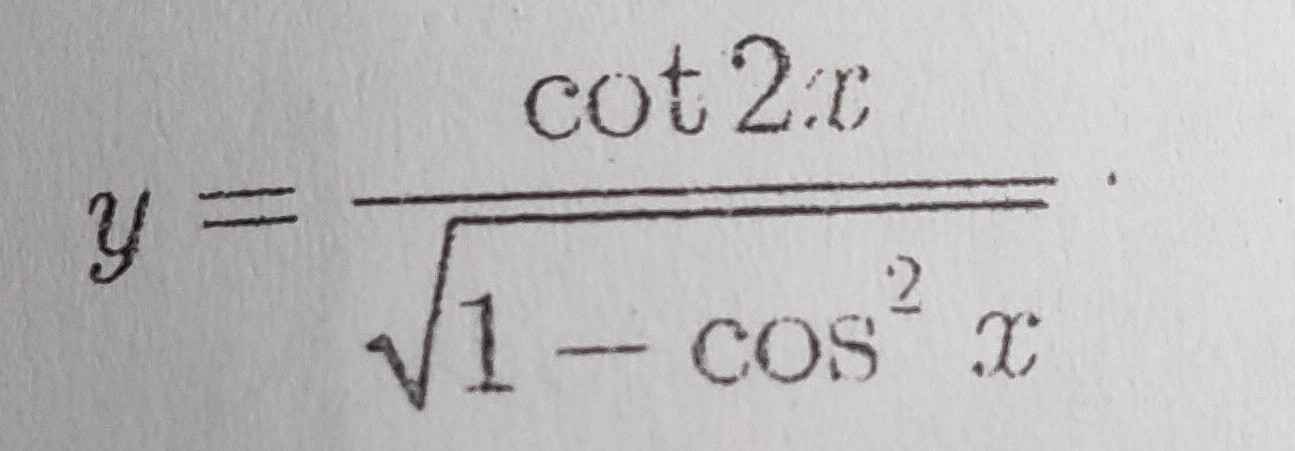
ĐKXĐ: \(\left\{{}\begin{matrix}2x< >k\Pi\\1-cos^2x>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x< >\dfrac{k\Pi}{2}\\cos^2x< 1\end{matrix}\right.\Leftrightarrow x< >\dfrac{k\Pi}{2}\)

ĐKXĐ: \(\dfrac{cosx-2}{1-sinx}>=0\)

\(\Leftrightarrow1-sinx< 0\)(Vì cosx-2<0) 

=>sin x>1(vô lý)

ĐKXĐ: \(\left\{{}\begin{matrix}2x< >\dfrac{\Pi}{2}+k\Pi\\\sin2x< >-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{\Pi}{4}+\dfrac{k\Pi}{2}\\2x\ne-\dfrac{\Pi}{2}+k2\Pi\end{matrix}\right.\Leftrightarrow x\notin\left\{\dfrac{\Pi}{4}+\dfrac{k\Pi}{2};-\dfrac{\Pi}{4}+k\Pi\right\}\)

ĐKXĐ: \(\left\{{}\begin{matrix}\tan^2x< >1\\\dfrac{2-\cos x}{1+\cos x}>=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne\pm\dfrac{\Pi}{4}+k\Pi\\\cos x< =2\end{matrix}\right.\)

\(\Leftrightarrow x\ne\pm\dfrac{\Pi}{4}+k\Pi\)

2)\(y=1-2.sin\dfrac{x}{2}.cos\dfrac{x}{2}+cos2x=1-sinx+\left(1-2sin^2x\right)\)

\(=-2sin^2x-sinx+2\)

Đặt \(t=sinx,t\in\left[-1;1\right]\)

Xét \(f\left(t\right)=-2t^2+2-t\)

Vẽ BBT(dạng như này, lười quá)

\(t\)              \(-1\)         \(-\dfrac{1}{4}\)        \(1\)

\(f\left(t\right)\)          \(1\)           \(\dfrac{17}{8}\)         \(-1\)

\(miny=minf\left(t\right)=-1\Leftrightarrow sinx=-1\)\(\Leftrightarrow x=-\dfrac{\pi}{2}+k2\pi\)

\(maxy=maxf\left(t\right)=\dfrac{17}{8}\Leftrightarrow sinx=-\dfrac{1}{4}\)\(\Leftrightarrow\left[{}\begin{matrix}x=arcsin\left(-\dfrac{1}{4}\right)+k2\pi\\x=\pi-arcsin\left(-\dfrac{1}{4}\right)+k2\pi\end{matrix}\right.\)

1)\(y=\left(sin^2x+cos^2x\right)^2-2sin^2x.cos^2x-4+cos2x\)

\(=-3-\dfrac{1}{2}sin^22x+cos2x\)

\(=-\dfrac{1}{2}\left(1-cos^22x\right)-3+cos2x\)

\(=\dfrac{1}{2}cos^22x+cos2x-\dfrac{7}{2}\)

Đặt \(t=cos2x,t\in\left[-1;1\right]\)

Xét \(f\left(t\right)=\dfrac{1}{2}t^2+t-\dfrac{7}{2}\), \(I\left(-1;-4\right)\)

Vẽ BBT, khoảng từ \(\left(-1;+vc\right)\) hàm \(f\left(t\right)\) đồng biến

\(miny=\min\limits_{\left[-1;1\right]}f\left(t\right)=-4\Leftrightarrow t=-1\Leftrightarrow cos2x=-1\) \(\Leftrightarrow x=\dfrac{\pi}{2}+k\pi\)

\(maxy=\max\limits_{\left[-1;1\right]}f\left(t\right)=-2\Leftrightarrow t=1\Leftrightarrow cos2x=1\)\(\Leftrightarrow x=k\pi\)

Vậy...

4)\(y=2\left(\dfrac{1}{2}sin2x-\dfrac{\sqrt{3}}{2}cos2x\right)+1\)\(=2\left(sin2x.cos\dfrac{\pi}{3}-cos2x.sin\dfrac{\pi}{3}\right)+1\)

\(=2sin\left(2x-\dfrac{\pi}{3}\right)+1\)

mà \(-2\le2sin\left(2x-\dfrac{\pi}{3}\right)\le2\)

\(\Leftrightarrow-1\le y\le3\)

\(miny=-1\Leftrightarrow sin\left(2x-\dfrac{\pi}{3}\right)=-1\)\(\Leftrightarrow x=-\dfrac{\pi}{12}+k\pi\)

\(maxy=3\Leftrightarrow sin\left(2x-\dfrac{\pi}{3}\right)=1\)\(\Leftrightarrow x=\dfrac{5\pi}{12}+k\pi\)

Vậy 

3: y=5*(3/5sinx+4/5cosx)-2

=5*sin(x+alpha)-2

-1<=sin(x+alpha)<=1

=>-5<=5*sin(x+alpha)<=5

=>-7<=y<=3

y=-7 khi sin(x+alpha)=-1

=>x+alpha=-pi/2+k2pi

=>x=-pi/2-alpha+k2pi

y=3 khi x+alpha=pi/2+k2pi

=>x=pi/2-alpha+k2pi

7: =>cosx+sinx+1=2y+y*cosx

=>sin x+cosx(1-y)=2y-1

Để phương trình có nghiệm thì 1^2+(1-y)^2>=(2y-1)^2

=>y^2-2y+2>=4y^2-4y+1

=>-3y^2+2y+1>=0

=>-1/3<=y<=1

=>y min=-1/3 và y max=1

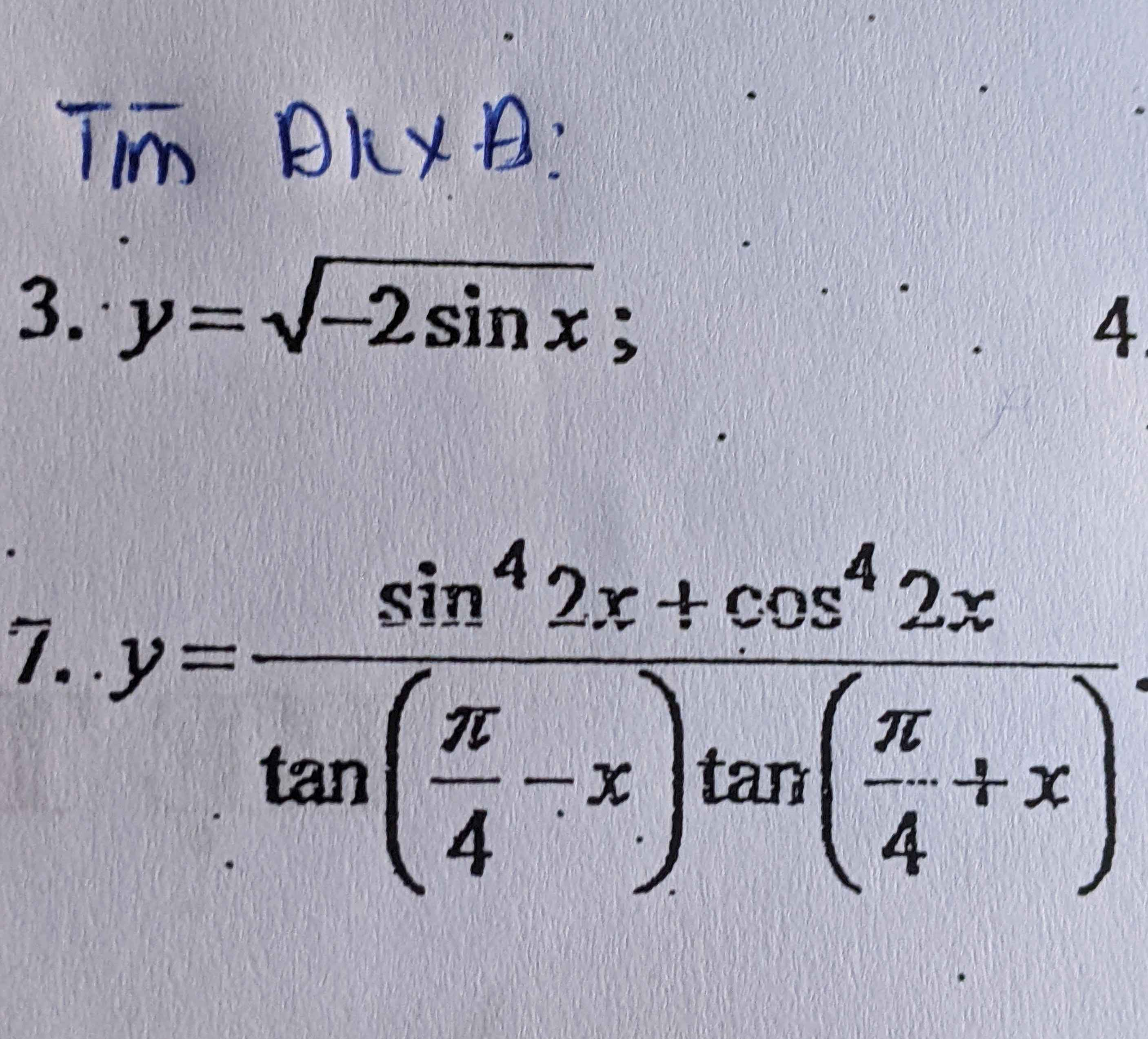
Câu 3 : 

Hàm số xác định khi sinx ≥ 0

⇔ \(k2\pi\le x\le\pi+k2\pi\) (nằm ở cung tròn phần dương của đường tròn lượng giác)

Câu 7

Hàm số xác định khi \(tan\left(x+\dfrac{\pi}{4}\right).tan\left(x-\dfrac{\pi}{4}\right)\ne0\)

⇔ \(\left\{{}\begin{matrix}tan\left(x-\dfrac{\pi}{4}\right)\ne0\\tan\left(x+\dfrac{\pi}{4}\right)\ne0\end{matrix}\right.\) ⇔ \(\left\{{}\begin{matrix}x-\dfrac{\pi}{4}\ne k\pi\\x+\dfrac{\pi}{4}\ne k\pi\end{matrix}\right.\)⇔ \(x\ne\pm\dfrac{\pi}{4}+k\pi\) với k là số nguyên

Ta có: \(sin^22x=\dfrac{1}{2}\Leftrightarrow\)\(\left[{}\begin{matrix}sin2x=\dfrac{1}{\sqrt{2}}\\sin2x=\dfrac{-1}{\sqrt{2}}\end{matrix}\right.\)\(\Leftrightarrow\)\(\left[{}\begin{matrix}\left[{}\begin{matrix}2x=\dfrac{\pi}{4}+k2\pi\\2x=\dfrac{3\pi}{4}+k2\pi\end{matrix}\right.\\\left[{}\begin{matrix}2x=\dfrac{-\pi}{4}+k2\pi\\2x=\dfrac{5\pi}{4}+k2\pi\end{matrix}\right.\end{matrix}\right.\)\(\Leftrightarrow\)\(\left[{}\begin{matrix}\left[{}\begin{matrix}x=\dfrac{\pi}{8}+k\pi\\x=\dfrac{3\pi}{8}+k\pi\end{matrix}\right.\\\left[{}\begin{matrix}x=\dfrac{-\pi}{8}+k\pi\\x=\dfrac{5\pi}{8}+k\pi\end{matrix}\right.\end{matrix}\right.\)

\(\Rightarrow x=\dfrac{\pi}{8}+\dfrac{k\pi}{4}\)

Refer:

\(\Leftrightarrow\dfrac{1}{2}-\dfrac{1}{2}cos4x=\dfrac{1}{2}\)

\(\Leftrightarrow cos4x=0\)

\(\Leftrightarrow4x=\dfrac{\pi}{2}+k\pi\)

\(\Leftrightarrow x=\dfrac{\pi}{8}+\dfrac{k\pi}{4}\)