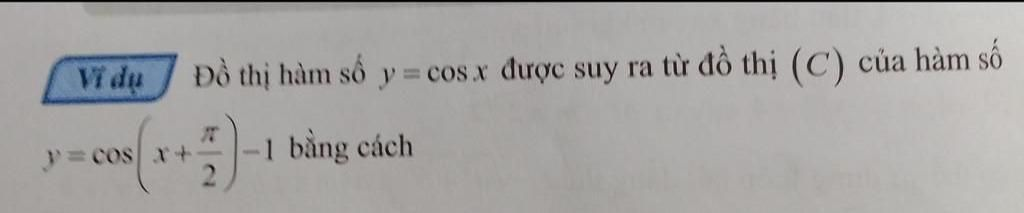
Bài 1: Hàm số lượng giác

Tịnh tiến \(y=cos\left(x+\dfrac{\pi}{2}\right)-1\) xuống dưới 1 đơn vị ta được \(y=cos\left(x+\dfrac{\pi}{2}\right)\)

Tịnh tiến \(t=cos\left(x+\dfrac{\pi}{2}\right)\) sang phải \(\dfrac{\pi}{2}\) đơn vị ta được đồ thị \(y=cosx\)

\(\Rightarrow\) B là đáp án đúng

Đề bài tào lao thật sự

Vừa độ vừa radian trong 1 phương trình là không chính xác. Đã độ thì độ hết, đã radian thì radian hết

16

16

30.

\(\left(1\right);\left(3\right)\)

\(sin4x+\sqrt{3}cos4x=2\)

\(\Leftrightarrow\dfrac{1}{2}sin4x+\dfrac{\sqrt{3}}{2}cos4x=1\)

\(\Leftrightarrow sin\left(4x+\dfrac{\pi}{3}\right)=1\)

\(\Leftrightarrow4x+\dfrac{\pi}{3}=k2\pi\)

\(\Leftrightarrow x=-\dfrac{\pi}{12}+\dfrac{k\pi}{2}\)

\(cosx=cos\alpha\)

\(\Leftrightarrow x=\pm\alpha+k2\pi\)

Lời giải:
ĐKXĐ: \(\left\{\begin{matrix} \cos 2x+1\neq 0\\ \sin x\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 2x\neq \pm \pi +2k\pi \\ x\neq n\pi \end{matrix}\right.\) với mọi $k,n\in\mathbb{Z}$

\(\Leftrightarrow \left\{\begin{matrix} x\neq \frac{k}{2}\pi, \text{k nguyên lẻ} \\ x\neq n\pi, \text{n nguyên bất kỳ} \end{matrix}\right.\)

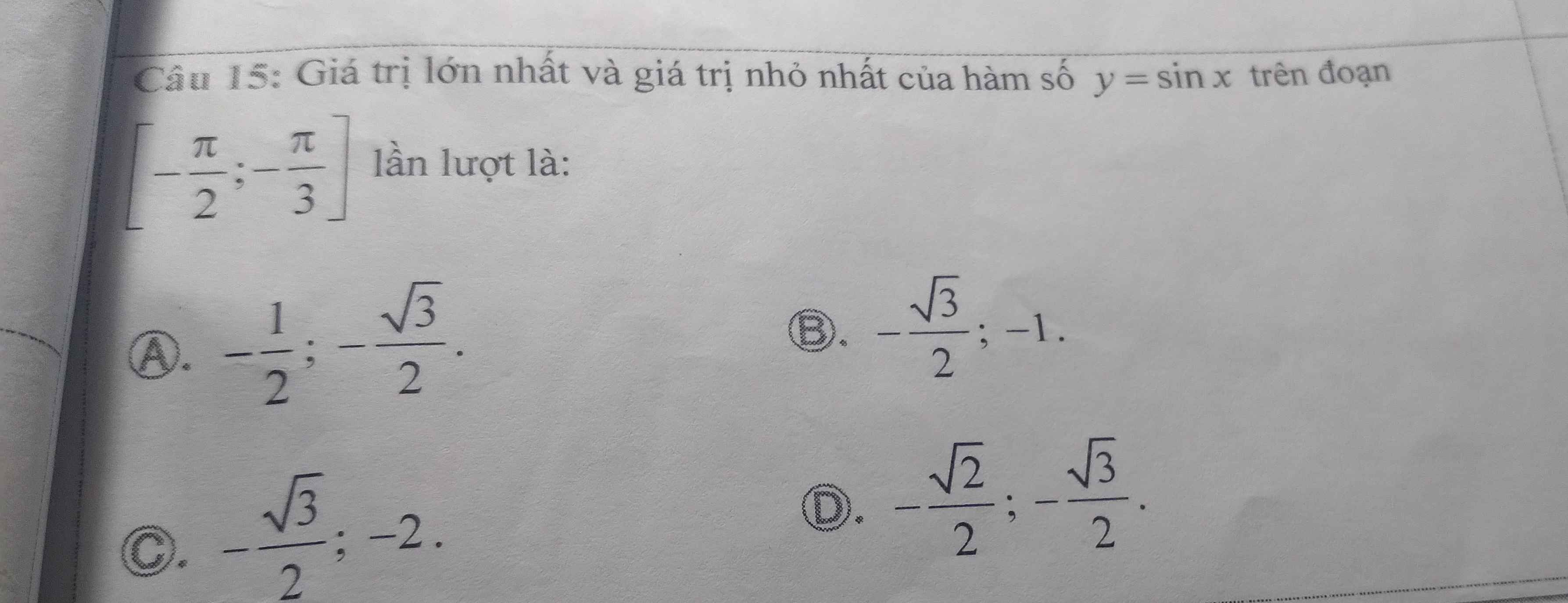
Lời giải:
Trong khoảng $[\frac{-\pi}{2}; \frac{-\pi}{3}]$ $x$ càng lớn thì $\sin x$ càng lớn 

Do đó:

$y_{\min}=y(\frac{-\pi}{2})=-1$ 

$y_{\max}=y(\frac{-\pi}{3})=\frac{-\sqrt{3}}{2}$