Bài 1: Hàm số lượng giác

a: \(VT=\dfrac{\left(sina+cosa\right)^3-3\cdot sina\cdot cosa\left(sina+cosa\right)}{sina+cosa}\)

=(sina+cosa)^2-3*sina*cosa

=sin^2a+cos^2a-sina*cosa

=1-sina*cosa=VP

c: VT=(sin^2a+cos^2a)^2-2*sin^2a*cos^2a-(sin^2a+cos^2a)^3+3*sin^2a*cos^2a*(sin^2a+cos^2a)

=1-2sin^2a*cos^2a-1+3*sin^2a*cos^2a

=sin^2a*cos^2a=VP

\(a,cos^4a-sin^4a=2cos^2a-1\\ VT=\left(cos^2a-sin^2a\right)\left(cos^2a+sin^2a\right)\\ =cos^2a-sin^2a\\ =cos2a=2cos^2a-1\)

\(b,VT=\dfrac{cos^2a+\dfrac{sin^2a}{cos^2a}-1}{sin^2a}\\ =\dfrac{\dfrac{cos^4a+sin^2a-cos^2a}{cos^2a}}{sin^2a}\\ =\dfrac{\dfrac{cos^4a+\left(1-cos^2a\right)-cos^2a}{cos^2a}}{sin^2a}\\ =\dfrac{\dfrac{cos^4a+1-2cos^2a}{cos^2a}}{sin^2a}\\ =\dfrac{\dfrac{\left(1-cos^2a\right)^2}{cos^2a}}{sin^2a}\\ =\dfrac{sin^4a}{cos^2a}:sin^2a\\ =\dfrac{sin^4a}{cos^2a}\times\dfrac{1}{sin^2a}\\ =\dfrac{sin^2a}{cos^2a}=tan^2a\)

ĐKXĐ: \(\left\{{}\begin{matrix}sinx\ne0\\6sin^2x-3\ne0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}sinx\ne0\\cos2x\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ne k\pi\\2x\ne\dfrac{\pi}{2}+k\pi\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x\ne k\pi\\x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\end{matrix}\right.\)

1: -1<=sin(x-pi/2)<=1

=>-2<=2sin(x-pi/2)<=2

=>1<=y<=5

y=1 khi sin(x-pi/2)=-1

=>x-pi/2=-pi/2+k2pi

=>x=k2pi

y=5 khi sin(x-pi/2)=1

=>x-pi/2=pi/2+k2pi

=>x=pi+k2pi

2: -1<=cos2x<=1

=>1/2>=-1/2cos2x>=-1/2

=>7/2>=y>=5/2

y=7/2 khi -1/2cos2x+3=7/2

=>-1/2cos2x=1/2

=>cos2x=-1

=>2x=-pi+k2pi

=>x=-pi/2+kpi

y=5/2 khi cos2x=1

=>2x=k2pi

=>x=kpi

3: -1<=sin2x<=1

=>-3<=3sin2x<=3

=>-8<=y<=-2

y=-8 khi sin2x=-1

=>2x=-pi/2+k2pi

=>x=-pi/4+kpi

y=-2 khi sin2x=1

=>2x=pi/2+k2pi

=>x=pi/4+kpi

4: -1<=cos(x+pi/4)<=1

=>2>=-2cos(x+pi/4)>=-2

=>9>=y>=5

y=9 khi -2cos(x+pi/4)+7=9

=>-2cos(x+pi/4)=2

=>cos(x+pi/4)=-1

=>x+pi/4=pi+k2pi

=>x=3/4pi+k2pi

y=5 khi cos(x+pi/4)=1

=>x+pi/4=k2pi

=>x=k2pi-pi/4

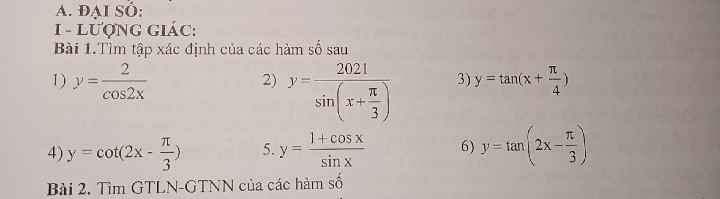
`1)` H/s xđ `<=>cos 2x \ne 0<=>2x \ne \pi/2+k\pi<=>x \ne \pi/4+k\pi/2`  `(k in ZZ)`

   `=>TXĐ: D=R\\{\pi/4+k\pi/2|k in ZZ}`

________________________________________

`2)` H/s xđ `<=>sin(x+\pi/3) \ne 0<=>x+\pi/3 \ne k\pi<=>x \ne -\pi/3+k\pi`  `(k in ZZ)`

  `=>TXĐ: D=R\\{-\pi/3+k\pi|k in ZZ}`

________________________________________

`3)` H/s xđ `<=>cos(x+\pi/4) \ne 0<=>x+\pi/4 \ne \pi/2+k\pi<=>x \ne \pi/4+k\pi`  `(k in ZZ)`

   `=>TXĐ: D=R\\{\pi/4+k\pi|k in ZZ}`

________________________________________

`4)` H/s xđ `<=>sin(2x-\pi/3) \ne 0<=>2x-\pi/3 \ne k\pi<=>x \ne \pi/6+k\pi/2`  `(k in ZZ)`

  `=>TXĐ: D=R\\{\pi/6+k\pi/2| k in ZZ}`

________________________________________

`5)` H/s xđ `<=>sin x \ne 0<=>x \ne k\pi`  `(k in ZZ)`

   `=>TXĐ: D=R\\{k\pi|k in ZZ}`

________________________________________

`6)` H/s xđ `<=>cos(2x-\pi/3) \ne 0<=>2x-\pi/3 \ne \pi/2+k\pi<=>x \ne [5\pi]/12+k\pi/2`  `(k in ZZ)`

   `=>TXĐ: D=R\\{[5\pi]/12+k\pi/2|k in ZZ}`

sin4x + \(\sqrt{3}\)cos4x = \(\sqrt{2}\)

lấy 2 vế chia cho \(\sqrt{2}\)

=> sin(4x+ \(\dfrac{pi}{6}\))=\(\dfrac{pi}{4}\)

rồi tự tính nha

=>(1+cos2x)/2-sin2x+7(1-cos2x)/2=5

=>1/2+1/2cos2x-sin2x+7/2-7/2cos2x=5

=>-sin2x-3cos2x=5-7/2-1/2=5-4=1

=>sin2x+3cos2x=-1

=>\(\dfrac{1}{\sqrt{10}}\cdot sin2x+\dfrac{3}{\sqrt{10}}\cdot cos2x=-\dfrac{1}{\sqrt{10}}\)

=>sin(2x+a)=-cosa=cos(pi-a)

=>sin(2x+a)=sin(pi/2-pi+a)=sin(a-pi/2)

=>2x+a=a-pi/2+k2pi hoặc 2x+a=3/2pi-a+k2pi

=>x=-pi/4+kpi hoặc x=3/4pi-a+kpi

\(y=\dfrac{1-cos\left(6x+\dfrac{2pi}{3}\right)}{2}+3x=\dfrac{1}{2}+3x-\dfrac{1}{2}cos\left(6x+\dfrac{2pi}{3}\right)\)

Chu kì là T=2pi/6=1/3pi