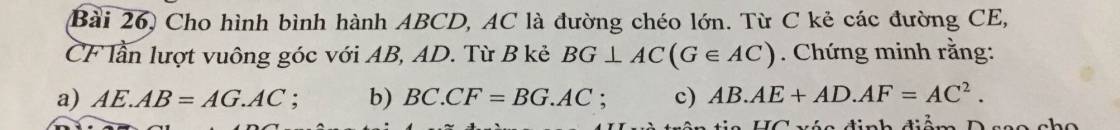Bài 1: Định lý Talet trong tam giác
a)Cho tam giác AEF có PQ//EF, biết DF=24cm, QF=15cm, DP=6,3cm. Tính PE b)cho tam giác MNK trên đoạn MN lấy điểm E, trên đoạn NK lấy điểm F sao cho EF//MK. Biết NE=5cm,MN=7,5cm, FK=2cm. Tính NF
a: D ở đâu vậy bạn?
b: EN+EM=MN
=>EM=7,5-5=2,5cm
Xét ΔNMK có EF//MK
nên NE/EM=NF/FK
=>NF/2=5/2,5=2
=>NF=4(cm)
Đúng 0
Bình luận (0)
Bài 4:Cho tam giác ABC có AB = 6cm, AC = 8cm , BC = 10cm. Lấy điểm D trên AB sao cho AD = 2cm. Qua D vẽ đường thẳng song song với BC cắt AC tại E. 1) Tính AE. 2) Qua E vẽ đường thẳng song song với AB và cắt BC tại F. Tính BF, DE. 3) Tính và so sánh các tỉ số : AD/AB , AE/AC , DE/BC
1: Xét ΔABC có DE//BC
nên AE/AC=AD/AB
=>AE/8=1/3
=>AE=8/3(cm)
2:
Xét ΔABC có DE//BC
nên DE/BC=AD/AB
=>DE/10=1/3
=>DE=10/3(cm)
Xét tứ giác BDEF có
BD//EF
BF//DE
Do đó: BDEF là hình bình hành
=>BF=DE=10/3(cm)
3:
AD/AB=1/3
AE/AC=1/3
DE/BC=1/3
Do đó: AD/AB=AE/AC=DE/BC
Đúng 0
Bình luận (0)
A)cho biết MN/HK=9/4,MN=18cm. Hãy tính HK
Ta có: \(\dfrac{MN}{HK}=\dfrac{9}{4}\)
\(\Rightarrow\dfrac{18}{HK}=\dfrac{9}{4}\)
\(\Rightarrow9.HK=18.4\)
\(\Rightarrow9HK=72\)
\(\Rightarrow HK=8cm\)
Đúng 1
Bình luận (0)
cho tam giá ABC vuông tại có AB=25 cm C=43 độ. Kẻ AH⊥BC
a, Tính AC
b, Tính AH
c, Tính BH,CH
Sửa đề: ΔABC vuông tại A
a: Xét ΔABC vuông tại A có
AB=AC*tan C
=>AC=25/tan43
=>\(AC\simeq26,81\left(cm\right)\)
b: Xét ΔAHC vuông tại H có
AH=AC*sin C
=>\(AH=26.81\cdot sin43\simeq18,28\left(cm\right)\)
c: \(CH=\sqrt{AC^2-AH^2}\simeq19,61\left(cm\right)\)
\(BH=\dfrac{AH^2}{HC}\simeq17,04\left(cm\right)\)
Đúng 3
Bình luận (0)
Trong tam giác ABC có AB = 6cm và B’C’// BC. Lấy trên cạnh AB điểm B’, trên cạnh AC lấy điểm C’ sao cho AB’ = 4cm; AC’ = 3cm. Tính độ dài cạnh AC.
Theo định lý Ta - let ta có:
\(\dfrac{AB'}{AB}=\dfrac{AC'}{AC}\)
\(\Leftrightarrow\dfrac{4}{6}=\dfrac{3}{AC}\)
\(\Rightarrow\dfrac{2}{3}=\dfrac{1}{AC}\)
\(\Rightarrow2AC=3\)
\(\Rightarrow AC=\dfrac{2}{3}\)
Đúng 1
Bình luận (0)
Cho tam giác ABC có AB = 9 cm ; AC = 12 cm ; BC = 16 cm. Trên BC lấy điểm D sao cho CD = 8 cm. Tính độ dài AD
CD=8cm=1/2BC
=>D là trung điểm của BC
Xét ΔABC có AD là trung tuyến
nên \(AD=\sqrt{\dfrac{9^2+12^2}{2}-\dfrac{16^2}{4}}=\dfrac{\sqrt{194}}{2}\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho hình thang ABCD(AB//CD,ABCD).Có O là giao điểm của 2 đường chéo.Qua O kẻ 2 đường thẳng song song với 2 đáy cắt AD tại M,cắt BC tại N.a) So sánh các tỉ số OM/CD và AO/AC,ON/CD và OB/BD.b) Chứng minh OMON.c) Tính MN biết AB4cm CD6cm.d) Gọi E là giao điểm của 2 đường thẳng AD và BC.Chứng minh E,O và trung điểm của BC thẳng hàng.e) Qua B kẻ đường thẳng song song với AD cắt AC tại K. Chứng minh OA mũ 2 OK*OC
Đọc tiếp
Cho hình thang ABCD(AB//CD,AB<CD).Có O là giao điểm của 2 đường chéo.Qua O kẻ 2 đường thẳng song song với 2 đáy cắt AD tại M,cắt BC tại N.
a) So sánh các tỉ số OM/CD và AO/AC,ON/CD và OB/BD.
b) Chứng minh OM=ON.
c) Tính MN biết AB=4cm CD=6cm.
d) Gọi E là giao điểm của 2 đường thẳng AD và BC.Chứng minh E,O và trung điểm của BC thẳng hàng.
e) Qua B kẻ đường thẳng song song với AD cắt AC tại K. Chứng minh OA mũ 2 = OK*OC
a: OM//CD
=>OM/CD=AO/AC=AM/AD
ON//DC
=>ON/CD=BO/BD=BN/BC
b: OM/CD=ON/CD(AM/AD=BN/BC)
=>OM=ON
c: 2/MN=1/AB+1/CD
=>2/MN=1/4+1/6=3/12+2/12=5/12
=>MN/2=12/5
=>MN=24/5=4,8cm
Đúng 1
Bình luận (2)
a: Xet ΔAEC vuông tại E và ΔAGB vuông tại G có
góc EAC chung
=>ΔAEC đồng dạng với ΔAGB
=>AE/AG=AC/AB
=>AE*AB=AG*AC
b: Xet ΔFAC vuông tại F và ΔGCB vuông tại G có
góc FAC=góc GCB
=>ΔFAC đồng dạng với ΔGCB
=>AC/CB=FC/BG
=>AC*BG=FC*CB
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC, vẽ các đường cao BD (De AC) và CE (E= AB). Biết AB = 10cm; AC = 12cm, BD = 8cm a/ Chứng minh: ABD AACE. b/ Tính độ dài đoạn thăng CE. c/ Tính diện tích AADE.
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc DAB chung
=>ΔADB đồng dạng với ΔAEC
b: ΔADB đồng dạng với ΔAEC
=>AD/AE=AB/AC=DB/EC
=>8/CE=10/12=5/6
=>CE=8:5/6=8*6/5=9,6cm
Đúng 0
Bình luận (0)