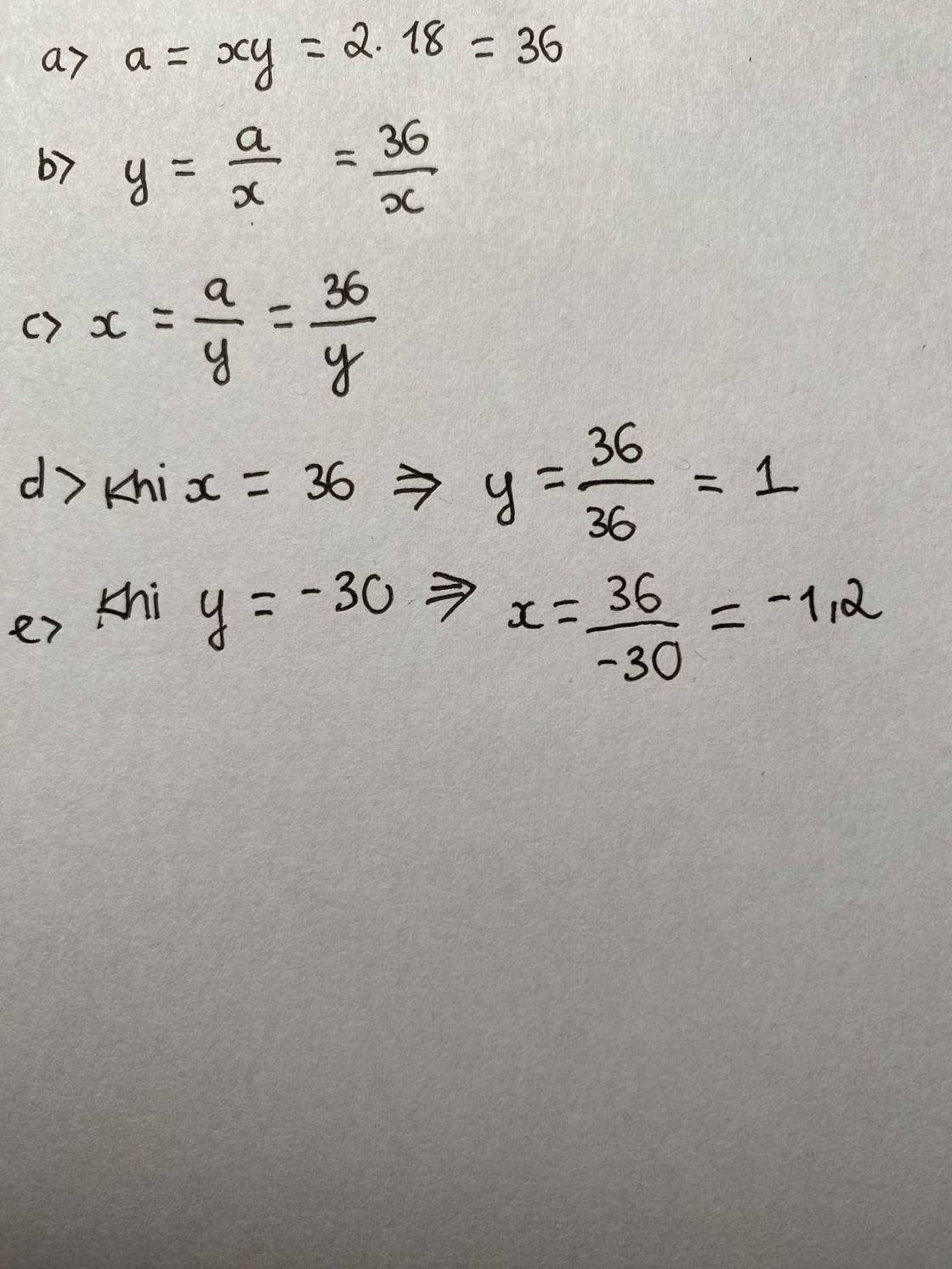Bài 1: Đại lượng tỷ lệ thuận

gọi chiều dài của cạnh 1 và cạnh 2 lần lượt là a,b(a,b>0)

tỉ số hai cạnh lần lượt là `2/3` `=> a/2 =b/3`

nửa chu vi hình chữ nhật lllaf

`20:2=10(m)`

áp dụng tính chất dảy tỉ số bằng nhau ta có

`a/2=b/3=(a+b)/(2+3)=10/5=2`

`=> a=2*2=4` `b=2*3=6`

diện tích hình chữ nhật là

`4*6=24(m^2)`

ds

Nửa chu vi HCN là:

\(20:2=10\left(m\right)\)

Chiều dài HCN là:

\(10:\left(2+3\right)\times3=6\left(m\right)\)

Chiều rộng HCN là:

\(10-6=4\left(m\right)\)

Diện tích hình chữ nhật là:

\(6\times4=24\left(m^2\right)\)

Nửa chu vi hình chữ nhật:
\(\dfrac{20}{2}=10\left(m\right)\)
Gọi x và y lần lượt là chiều dài của hình chữ nhật.
Ta được:
\(\dfrac{x}{y}=\dfrac{2}{3}\) và \(x+y=10\)
\(\dfrac{x}{y}=\dfrac{2}{3}\)
\(\Rightarrow3x=2y\)
\(\Rightarrow\dfrac{x}{2}=\dfrac{y}{3}\)
Áp dụng tính chất của dãy tỉ số bằng nhau,ta có:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{x+y}{2+3}=\dfrac{10}{5}=2\)
\(\Rightarrow x=2\cdot2=4\)
     \(y=2\cdot3=6\)
Diện tích hình chữ nhật là:
\(4\cdot6=24\left(m^2\right)\)

Gọi số quyển vở mà An, bình, Cường nhận lần lượt là a,b,c

Theo đề, ta có: a/3=b/4=c/5 và a+b+c=48

Áp dụng tính chất của DTSBN, ta được:

\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{3+4+5}=\dfrac{48}{12}=4\)

=>a=12; b=16; c=20

Gọi x (quyển), y (quyển), z (quyển) lần lượt là số quyển vở của An, Bình, Cường nhận được (x, y, z \(\in\) N^*)

Do số quyển vở của An, Bình, Cường tỉ lệ thuận với 3; 4; 5 nên:

\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}\)

Do tổng số quyển vở là 48 nên:

\(x+y+z=48\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}=\dfrac{x+y+z}{3+4+5}=\dfrac{48}{12}=4\)

\(\dfrac{x}{3}=4\Rightarrow x=4.3=12\)

\(\dfrac{y}{4}=4\Rightarrow y=4.4=16\)

\(\dfrac{z}{5}=4\Rightarrow z=4.5=20\)

Vậy An nhận được 12 quyển vở

Bình nhận được 16 quyển vở

Cường nhận được 20 quyển vở

a: x và y tỉ lệ thuận

nên x1/y1=x2/y2

=>\(\dfrac{x1}{y1}=\dfrac{x2}{y2}=\dfrac{x_1+2x_2}{y_1+2y_2}=\dfrac{2}{8}=\dfrac{1}{4}\)

=>x=1/4y

=>y=4x

b: y=16

=>4x=16

=>x=4

Bài 6:

Gọi độ dài hai cạnh lần lượt là a,b

Theo đề, ta có: a/3=b/5 và a+b=24

Áp dụng tính chất của DTSBN, ta được:

\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{a+b}{3+5}=\dfrac{24}{8}=3\)

=>a=9; b=15

Gọi khối lượng thanh 1 và thanh 2 lần lượt là a,b

Theo đề, ta có: a/2,7=b/7,8 và a+b=1102,5

Áp dụng tính chất của DTSBN, ta được:

\(\dfrac{a}{2.7}=\dfrac{b}{7.8}=\dfrac{a+b}{2.7+7.8}=\dfrac{1102.5}{10.5}=105\)

=>a=283,5; b=819

x tỉ lệ thuận với y theo hệ số k

=>x=ky

=>y=x/k

y tỉ lệ thuận vơi z theo hệ số a

=>y=az

=>x/k=az

=>x=z*ak

=>x tỉ lệ thuận với z theo hệ số tỉ lệ a*k

Bài 5:

a: Xét tứ giác ABEC có

I là trung điểm chung của AE và BC

=>ABEC là hình bình hành

=>AB=EC

b: Vì ABEC là hình bình hành

nên AC//BE

c: Xét tứ giác AMEN có

AM//EN

AM=EN

Do đó; AMEN là hình bình hành

=>AE cắt NM tại trung điểm của mỗi đường

=>M,I,N thẳng hàng

Bài 2:

a: Áp dụng tính chất của DTSBN, ta được:

\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{x+y}{2+3}=\dfrac{30}{5}=6\)

=>x=12; y=18

b: Đặt x/2=y/3=k

=>x=2k; y=3k

xy=54

=>6k^2=54

=>k^2=9

TH1: k=3

=>x=6; y=9

TH2: k=-3

=>x=-6; y=-9

c: x/2=y/3

=>x/8=y/12

y/4=z/5

=>y/12=z/15

=>x/8=y/12=z/15

Áp dụng tính chất của DTSBN, ta được:

\(\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}=\dfrac{3x+2y-4z}{3\cdot8+2\cdot12-4\cdot15}=\dfrac{-24}{-12}=2\)

=>x=16; y=24; z=30

d: 2x=3y=4z

=>x/6=y/4=z/3=k

=>x=6k; y=4k; z=3k

\(A=\dfrac{5x+7y-3z}{3x-2y+5z}\)

\(=\dfrac{30k+28k-9k}{18k-8k+15k}=\dfrac{49}{25}\)

tách ra bn nhé

a) \(3,7:4,5=\dfrac{3,7}{4,5}=\dfrac{37}{45}\)

b) \(2\dfrac{1}{3}:4\dfrac{2}{3}=\dfrac{7}{3}:\dfrac{14}{3}=\dfrac{7}{3}\times\dfrac{3}{14}=\dfrac{1}{2}\)

c) \(\dfrac{3}{8}:0,7=\dfrac{3}{8}:\dfrac{7}{10}=\dfrac{3}{8}\times\dfrac{10}{7}=\dfrac{15}{28}\)

d) \(5\dfrac{1}{7}:2\dfrac{1}{3}=\dfrac{36}{7}:\dfrac{7}{3}=\dfrac{36}{7}\times\dfrac{3}{7}=\dfrac{108}{49}\)

32,40,48