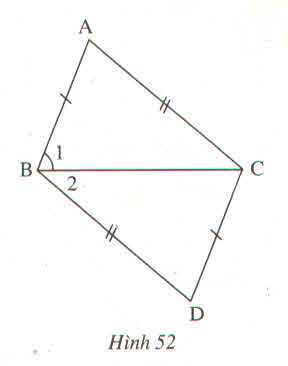
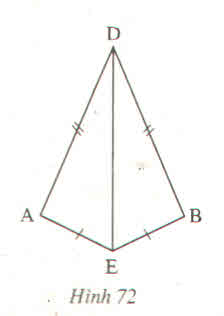
Xét bài toán : " \(\Delta AMB\) và \(\Delta ANB\) có MA = MB, NA = NB (h.71)
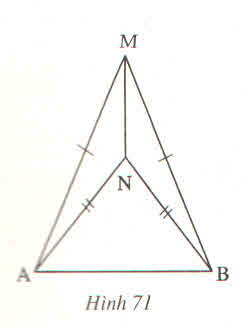
Chứng minh rằng : \(\widehat{AMN}=\widehat{BMN}\)
1) Hãy ghi giả thiết và kết luận của bài toán
2) Hãy sắp xếp bốn câu sau đây một cách hợp lí để giải bài toàn trên
a) Do đó \(\Delta AMN=\Delta BMN\) (c.c.c)
b) MN : cạnh chung
MA = MB (giả thiết)
NA = NB (giả thiết)
c) Suy ra \(\widehat{AMN}=\widehat{BMN}\) (hai góc tương ứng)
a) \(\Delta AMN=\Delta BMN\) có :
Xét tg AMN và tg BMN có:
MN chung
MA = MB (gt)
NA = NB (gt)
=> tg AMN = tg BMN (c.c.c)
1) Giả thiết: \(\Delta AMN;\Delta BMN\) có: MA = MB và NA = NB.
Kết luận: tg AMN = tg BMN
2) \(\Delta AMN\) và \(\Delta BMN\) có:
MN: cạnh chung
MA = MB (giả thiết)
NA = NB (giả thiết)
Do đó \(\Delta AMN=\Delta BMN\left(c.c.c\right)\)
Suy ra \(\widehat{AMN}=\widehat{BMN}\) (2 góc t/ư).