Đặt k =  . Ta có x = 2k, y = 5k
. Ta có x = 2k, y = 5k
Từ xy=10. suy ra 2k.5k = 10 => 10 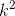 = 10 =>
= 10 => 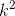 = 1 => k = ± 1
= 1 => k = ± 1
Với k = 1 ta được  = 1 suy ra x = 2, y = 5
= 1 suy ra x = 2, y = 5
Với k = -1 ta được  = -1 suy ra x = -2, y = -5
= -1 suy ra x = -2, y = -5
Gọi \(\dfrac{x}{2}=\dfrac{y}{5}=k\)
Với \(\dfrac{x}{2}=k\Rightarrow x=2k\); \(\dfrac{y}{5}=k\Rightarrow y=5k\)
Theo đề bài,ta còn có:
\(xy=10\)
hay 2k.5k=10
10k2 =10
\(\Rightarrow k=\pm1\)
Với k=1 \(\Rightarrow\dfrac{x}{2}=\dfrac{y}{5}=1\Rightarrow x=2;y=5\)
Với k=-1 \(\Rightarrow\dfrac{x}{2}=\dfrac{y}{5}=-1\Rightarrow x=-2;y=-5\)
Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
\(\Rightarrow\) \(a=b\cdot k\) và \(c=d\cdot k\)
ta có:
\(\dfrac{a+b}{a-b}=\dfrac{bk+b}{bk-b}=\dfrac{b\cdot k+b\cdot1}{b\cdot k-b\cdot1}=\dfrac{b\cdot\left(k+1\right)}{b\cdot\left(k-1\right)}=\dfrac{k+1}{k-1}\)\(\dfrac{c+d}{c-d}=\dfrac{dk+b}{dk-b}=\dfrac{d\cdot k+d\cdot1}{d\cdot k+d\cdot1}=\dfrac{d\cdot\left(k+1\right)}{d\cdot\left(k-1\right)}=\dfrac{k+1}{k-1}\)
\(\Rightarrow\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}\left(=\dfrac{k+1}{k-1}\right)\)
cho mk xin lỗi, bây giờ mk làm lại nha
Đặt \(\dfrac{x}{2}=\dfrac{y}{5}=k\)
\(\Rightarrow\) x = 2k và y = 5k vào x \(\cdot\) y = 10
ta có: 2k \(\cdot\)5k = 10k
\(\Leftrightarrow\)10k\(^2\) = 10
\(\Leftrightarrow k^2=10\div10\)
\(\Leftrightarrow k^2=1\)
\(\Rightarrow k=\pm1\)
-Với k = 1, ta được:
x = 2k = 2\(\cdot\)1 = 2 và y = 5k = 5.1 = 5
-Với k = -1, ta được:
x = 2k = 2.(-1) = -2 và y = 5k = 5.(-1) = -5
Ta có \(\dfrac{x}{2}=\dfrac{y}{5}\)
\(\Rightarrow\dfrac{x}{2}.\dfrac{y}{5}=\dfrac{x}{2}.\dfrac{x}{2}=\dfrac{y}{5}.\dfrac{y}{5}\)
\(\Rightarrow\dfrac{x.y}{10}=\dfrac{x^2}{4}=\dfrac{y^2}{25}\)
Mà xy=10
\(\Rightarrow\dfrac{x^2}{4}=\dfrac{y^2}{25}=\dfrac{10}{10}\)
\(\Rightarrow\dfrac{x^2}{4}=\dfrac{y^2}{25}=1\)
Với \(\dfrac{x^2}{4}=1\Rightarrow x^2=4\Rightarrow x=\pm4\)
\(\dfrac{y^2}{25}=1\Rightarrow y^2=25\Rightarrow y=\pm5\)
Mà x,y phải cùng dấu
Vậy............


