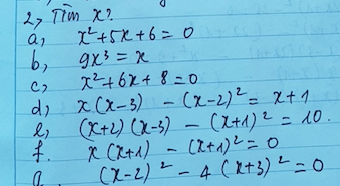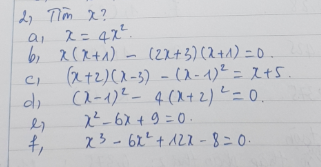2) Tìm x:
a) \(x^2+5x+6=0\)
⇒\(x^2+2x+3x+6=0\)
⇒\(\left(x^2+2x\right)+\left(3x+6\right)=0\)
⇒\(\left(x.x+2.x\right)+\left(3.x+3.2\right)=0\)
⇒\(x.\left(x+2\right)+3.\left(x+2\right)=0\)
⇒\(\left(x+2\right).\left(x+3\right)=0\)
⇒\(x+2=0\) \(hoặc\) \(x+3=0\)
\(+\))\(x+2=0\) \(+\))\(x+3=0\)
⇔\(x=-2\) ⇔\(x=-3\)
\(Vậy\) \(x\in\left\{-3;-2\right\}\)
c)\(x^2+6x+8=0\)
⇒ \(x^2+4x+2x+8=0\)
⇒ \(\left(x^2+4x\right)+\left(2x+8\right)=0\)
⇒ \(\left(x.x+4.x\right)+\left(2.x+2.4\right)=0\)
⇒ \(x.\left(x+4\right)+2.\left(x+4\right)=0\)
⇒ \(\left(x+4\right).\left(x+2\right)=0\)
⇒\(x+4=0\) \(hoặc\) \(x+2=0\)
\(+\)) \(x+4=0\) \(+\)) \(x+2=0\)
⇔\(x=-4\) ⇔\(x=-2\)
\(Vậy\) \(x\in\left\{-4;-2\right\}\)
a) x2+5x+6=0
⇒x2+2x+3x+6=0
⇒(x2+2x)+(3x+6)=0
⇒x(x+2)+3(x+2)=0
⇒(x+2)(x+3)=0
\(\Rightarrow\left[{}\begin{matrix}x+2=0\\x+3=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-2\\x=-3\end{matrix}\right.\)
b) 9x3=x
⇒9x3-x=0
⇒9x(x2-1)=0
⇒\(\left[{}\begin{matrix}9x=0\\x^2-1=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x^2=1\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=0\\x=\pm1\end{matrix}\right.\)
c) x2+6x+8=0
⇒ x2+2x+4x+8=0
⇒ (x2+2x)+(4x+8)=0
⇒ x(x+2)+4(x+2)=0
⇒ (x+2)(x+4)=0
\(\Rightarrow\left[{}\begin{matrix}x+2=0\\x+4=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=-2\\x=-4\end{matrix}\right.\)
d) x(x-3)-(x-2)2=x+1
⇒x2-3x-x2+4x-4=x+1
⇒x2-3x-x2+4x-4-x-1=0
⇒-5=0(vô lí)
e) (x+2)(x+3)-(x+1)2=0
⇒x2+5x+6-x2-2x-1=0
⇒3x+5=0
⇒3x=-5
⇒x=\(-\dfrac{5}{3}\)
f)x(x+1)-(x+1)2=0
⇒(x-x-1)(x+1)=0
⇒-1(x+1)=0
⇒x+1=0
⇒x=-1
g) (x-2)2-4(x+3)2=0
⇒x2-4x+4-4(x2+6x+9)=0
⇒x2-4x+4-4x2-24x-36=0
⇒-3x2-28x-32=0
đến đây mik chx bt lm