Bài tập 1:
a. $x^2-8x+16=x^2-2.4x+4^2=(x-4)^2$
b. $\frac{4}{25}x^2-9y^2=(\frac{2x}{5})^2-(3y)^2$
$=(\frac{2x}{5}-3y)(\frac{2x}{5}+3y)$
c.
$x^2-4xy+xy-4y^2=x(x-4y)+y(x-4y)=(x-4y)(x+y)$
d.
$x^2-2x+1-9y^2+6yz-z^2$
$=(x^2-2x+1)-(9y^2-6yz+z^2)$
$=(x-1)^2-(3y-z)^2=(x-1-3y+z)(x-1+3y-z)$
Bài tập 2:
a. Xét tam giác $ADM$ và $CBN$ có:
$AD=BC$
$\widehat{AMD}=\widehat{CNB}=90^0$
$\widehat{ADM}=\widehat{CBN}$ (so le trong)
$\Rightarrow \triangle ADM=\triangle CBN$ (ch-gn)
$\Rightarrow AM=CN$
Mà $AM\parallel CN$ (cùng vuông góc $BD$)
$\Rightarrow AMCN$ là hình bình hành
b. Vì $ABCD$ là hình bình hành nên $AC, BD$ cắt nhau tại trung điểm mỗi đường
Mà $O$ là trung điểm $BC$ nên $AC, BD$ cắt nhau tại $O$
$\Rightarrow A,O,C$ thẳng hàng.
c.
$K$ là trung điểm $AB$ thì $AK=\frac{1}{2}AB$
Tương tự $CI = \frac{1}{2}CD$
Mà $AB=CD$ nên AK=CI$
$AK\parallel CI$ do $AB\parallel CD$
Do đó $AKCI$ là hình bình hành
$\Rightarrow AI\parallel CK$





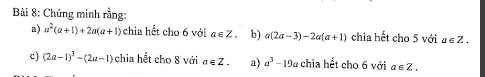

 Giúp em câu này vs ạ
Giúp em câu này vs ạ