a) \(3x\left(x-2\right)-x+2=0\)
\(3x\left(x-2\right)-\left(x-2\right)=0\)
\(\left(x-2\right)\left(3x-1\right)=0\)
⇔\(\left[{}\begin{matrix}x-2=0\\3x-1=0\end{matrix}\right.\)
⇔\(\left[{}\begin{matrix}x=2\\x=\dfrac{1}{3}\end{matrix}\right.\)
b) \(x\left(x-2\right)-2\left(x-2\right)=0\)
\(\left(x-2\right)\left(x-2\right)=0\)
\(\left(x-2\right)^2=0\)
⇔\(x-2=0\)
⇔\(x=2\)
Đúng 0
Bình luận (0)
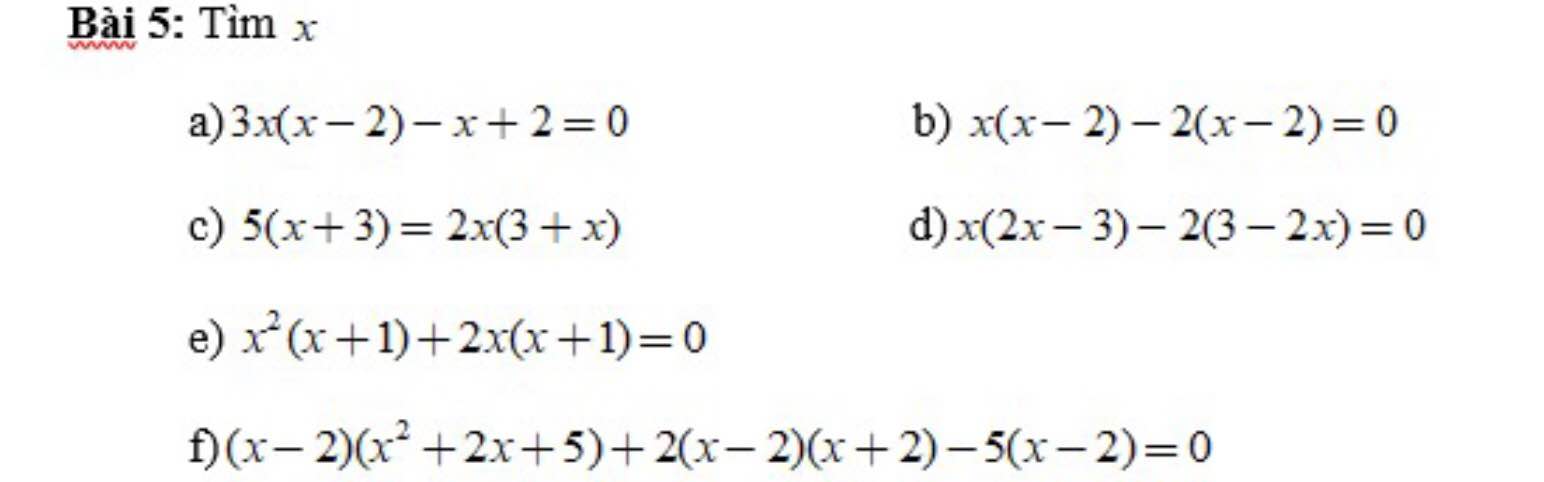 giải hết dùm em nha
giải hết dùm em nha
