Theo đề bài ta có x = , y =
( a, b, m ∈ Z, m > 0)
Vì x < y nên ta suy ra a< b
Ta có : x = , y =
; z =
Vì a < b => a + a < a +b => 2a < a + b
Do 2a< a +b nên x < z (1)
Vì a < b => a + b < b + b => a + b < 2b
Do a+b < 2b nên z < y (2)
Từ (1) và (2) ta suy ra x < z< y
Hãy chứng tỏ rằngGiả sử x = ; y = ( a, b, m Z, b # 0) và x < y. Hãy chứng tỏ rằng nếu chọn z =∈ thì ta có x < z < yLời giải:Theo đề bài ta có x = , y = ( a, b, m Z, m > 0)∈Vì x < y nên ta suy ra a< bTa có : x = , y = ; z = Vì a < b => a + a < a +b => 2a < a + b
Theo đề bài ta có x = , y =
( a, b, m ∈ Z, m > 0)
Vì x < y nên ta suy ra a< b
Ta có : x = , y =
; z =
Vì a < b => a + a < a +b => 2a < a + b
Do 2a< a +b nên x < z (1)
Vì a < b => a + b < b + b => a + b < 2b
Do a+b < 2b nên z < y (2)
Từ (1) và (2) ta suy ra x < z< y
Lời giải:
Theo đề bài ta có x = , y =
( a, b, m ∈ Z, m > 0)
Vì x < y nên ta suy ra a< b
Ta có : x = , y =
; z =
Vì a < b => a + a < a +b => 2a < a + b
Do 2a< a +b nên x < z (1)
Vì a < b => a + b < b + b => a + b < 2b
Do a+b < 2b nên z < y (2)
Từ (1) và (2) ta suy ra x < z< y
Ta có:x=\(\dfrac{a}{b}\) ;y=\(\dfrac{b}{m}\) (a,b,m \(\in\) Z.m>0) và x<y
Vì x<y nên a<b hay am<bm
Chung minh1:x<z hay \(\dfrac{a}{m}\) <\(\dfrac{a+b}{2m}\)
ta có:
am<bm\(\Rightarrow\) am+am<bm+am
\(\Rightarrow\) 2am<(b+a)m
\(\Rightarrow\) 2a<b+a
\(\Rightarrow\) \(\dfrac{2a}{2m}\) <\(\dfrac{b+a}{2m}\)
\(\Rightarrow\) \(\dfrac{a}{m}\) <\(\dfrac{b+a}{2m}\) hay x<z
Chứng minh 2:z<y hay \(\dfrac{a+b}{2m}\) <\(\dfrac{b}{m}\)
Ta có:
am<bm\(\Rightarrow\) am+bm<bm+bm
\(\Rightarrow\) (a+b)m<2bm
\(\Rightarrow\) a+b<2b
\(\Rightarrow\) \(\dfrac{a+b}{2m}\) <\(\dfrac{2b}{2m}\)
\(\Rightarrow\) \(\dfrac{a+b}{2m}\) < \(\dfrac{b}{m}\) hay z<y
Từ hai phần chứng minh trên, ta kết luận:x<z<y
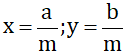(a, b, m ∈ Z; m > 0) và x < y. Hãy chứng minh nếu chọn 
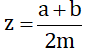thì ta có x < z < y.