Bài 3:
a: \(=\dfrac{\left(x+3\right)^2}{x+3}=x+3\)
b: \(=\dfrac{\left(3x-1\right)\left(3x+1\right)}{3x-1}=3x+1\)
c: \(=\dfrac{\left(2x+1\right)\left(4x^2-2x+1\right)}{2x+1}=4x^2-2x+1\)
d: \(=\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{-\left(x-1\right)}=-x^2-x-1\)
Bài 4
a) Để phép chia thực hiện được thì:
\(n\ge5\) và \(n+2\ge8\)
*) \(n+2\ge8\)
\(n\ge8-2\)
\(n\ge6\)
Vậy \(n\ge6\) thì phép chia thực hiện được
b) Để phép chia thực hiện được thì:
\(n+3\ge7\) và \(4\ge n\)
*) \(n+3\ge7\)
\(n\ge7-3\)
\(n\ge4\)
Kết hợp \(4\ge n\) và \(n\ge4\) \(\Rightarrow n=4\)
Vậy n = 4 thì phép chia thực hiện được




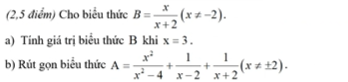
 cứu với mn
cứu với mn