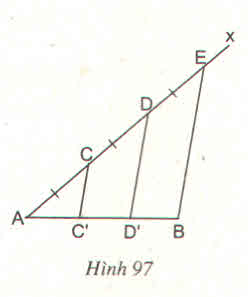
Xét tam giác \(ADD_1\) có AC=DC(gt); \(CC_1\text{//}DD_1\) ta có:
\(AC_1=D_1C_1\) (theo tính chất của đường trung bình của tam giác)
Xét hình thang \(CEBC_1\) có CD=ED(gt); \(DD_1\text{//}BE\) ta có:
\(C_1D_1=BD_1\) (theo tính chất của đường trung bình của hình thang)
Do đó \(AC_1=C_1D_1=D_1B\) (đpcm)
Chúc bạn học tốt!!! (bạn sửa hết \(C_1;D_1\) thành C'; D' hộ mình nha!)