Question

Cho đoạn thẳng AB. Kẻ tia Ax bất kì. Trên tia Ax lấy các điểm C,D,E sao cho AC = CD = DE. Kẻ đoạn thẳng EB. Qua C,D kẻ các đường thẳng song song với EB cắt AB lần lượt tại C' , D'. Chứng minh: AC' = C'D' = D'B.

* Vẽ hình rồi chứng minh giùm mình nha

Answer 1

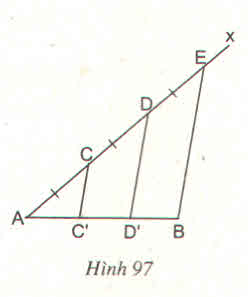
Xét tam giác ADD' , có :

. C trung điểm AD ( AC = CD ; C thuộc AD )

. CC' // DD' ( // BE )

. C' thuộc AD' ( CC' cắt AD' tại C' )

Suy ra : C' là trung điểm AD'

=> AC' = C'D' ( 1 )

Xét hình thang CC'BE ( CC' // BE ) , có :

. D' là trung điểm BC'

. DD' // BE // CC' ( cmt )

. D' thuộc BC'( DD' cắt BC' tại D' )

Suy ra : D' là trung điểm BC'

=> BD' = C'D' ( 2 )

Từ ( 1 ) và ( 2 ) , cho : AC' = C'D' = D'B