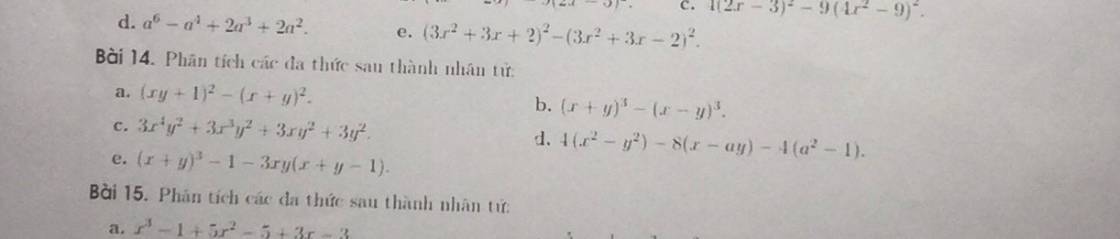\(a,\left(xy+1\right)^2-\left(x+y\right)^2\\ =\left(xy+1-x-y\right)\left(xy+1+x+y\right)\\ =\left(x-1\right)\left(y-1\right)\left(x+1\right)\left(y+1\right)\\ b,\left(x+y\right)^3-\left(x-y\right)^3\\ =2y\left(x^2+2xy+y^2+x^2-y^2+x^2+2xy+y^2\right)\\ =2y\left(3x^2+y^2\right)\)
\(c,3x^4y^2+3x^3y^2+3xy^2+3y^2\\=3y^2\left(x^4+x^3+x+1\right)\\ =3y^2\left(x+1\right)^2\left(x^2-x+1\right) \\ d,4\left(x^2-y^2\right)-8\left(x-ay\right)-4\left(a^2-1\right)\\ =-4\left(a^2-2ay+y^2\right)+4\left(x^2-2x+1\right)\\ =4\left(x-1\right)^2-4\left(a-y\right)^2\\ =4\left(x+y-a-1\right)\left(x-y+a-1\right)\)
\(e,\left(x+y\right)^3-1-3xy\left(x+y-1\right)\\ =\left(x+y-1\right)\left(x^2+x+y^2+y+2xy+1\right)-3xy\left(x+y-1\right)\\ =\left(x+y-1\right)\left(x^2+x+y^2+y-xy+1\right)\)