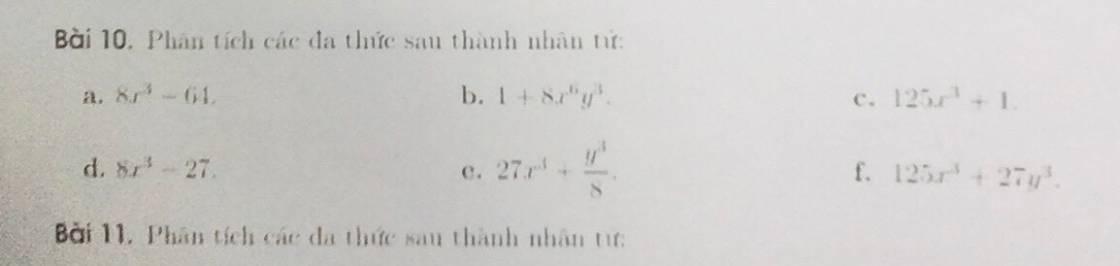\(a,8x^3-64\\ =8\left(x^3-8\right)\\ =8\left(x-2\right)\left(x^2+2x+4\right)\\ b,1+8x^6y^3\\ =\left(2x^2y+1\right)\left(4x^4y^2-2x^2y+1\right)\\ c,125x^3+1\\ =\left(5x+1\right)\left(25x^2+5x+1\right)\\ d,8x^3-27\\ =\left(2x-3\right)\left(4x^2+6x+9\right)\\ e,27x^3+\dfrac{y^3}{8}\\ =\left(3x+\dfrac{y}{2}\right)\left(9x^2+\dfrac{3}{2}xy+\dfrac{y^2}{4}\right)\\ f,125x^3+27y^3\\ =\left(5x+3y\right)\left(25x^2+15xy+9y^2\right)\)
Đúng 3
Bình luận (0)